这篇“离散格子的傅里叶变换和反傅里叶变换”提到两种傅里叶变换方法(两种规范):
“傅里叶变换时坐标可以用实际原子坐标,也可以用元胞坐标。用原子坐标时,傅里叶变量元胞内有些跃迁项会增加相位,即 ![]() ;而用元胞坐标时,傅里叶变换元胞内就没有增加相位,即
;而用元胞坐标时,傅里叶变换元胞内就没有增加相位,即 ![]() 。两种方法计算的结果是一样的,但建议用元胞坐标,会更方便些,尤其是当元胞比较大的时候会简单很多。”
。两种方法计算的结果是一样的,但建议用元胞坐标,会更方便些,尤其是当元胞比较大的时候会简单很多。”
核心区别:本质是“是否显式保留元胞内自由度”。元胞规范通过规范变换将元胞内自由度“打包”,在能带理论下会更加直观一些。
这里以 SSH 模型为例子进行说明。这是之前的一篇:SSH模型的哈密顿量、能带图和卷绕数(附Python代码)。示意图为:

实空间哈密顿量:
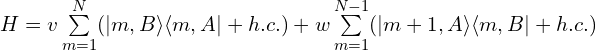
一、以元胞为单元的傅里叶变换
傅里叶变换过程参考:离散格子的傅里叶变换和反傅里叶变换。
第一项傅里叶变换后得到:
![]()
第二项傅里叶变换后得到:
![]()
其中,a 为原子间距。令 2a=1,因此哈密顿量写为:
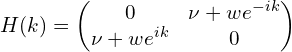
二、以原子为单元的傅里叶变换
第一项傅里叶变换后得到:
![]()
第二项傅里叶变换后得到:
![]()
其中,a 为原子间距。 令 2a=1,因此哈密顿量写为:
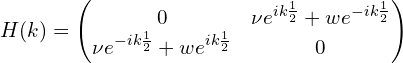
三、在键长相同的情况下本征值等价验证
(1)表达式验证
参考“由泡利矩阵组成的哈密顿量的本征值”,第一个哈密顿量形式的本征值为:
![]()
第二个哈密顿量形式的本征值:

(2)数值验证
代码如下(可以用到开源软件包 Guan:https://py.guanjihuan.com):
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/16199
"""
import numpy as np
from math import *
import cmath
def hamiltonian_1(k, v=0.6, w=1):
matrix = np.zeros((2, 2), dtype=complex)
matrix[0,1] = v+w*cmath.exp(-1j*k)
matrix[1,0] = v+w*cmath.exp(1j*k)
return matrix
def hamiltonian_2(k, v=0.6, w=1):
matrix = np.zeros((2, 2), dtype=complex)
matrix[0,1] = v*cmath.exp(1j*k/2)+w*cmath.exp(-1j*k/2)
matrix[1,0] = v*cmath.exp(-1j*k/2)+w*cmath.exp(1j*k/2)
return matrix
def main():
k_array = np.linspace(-pi ,pi, 100)
E_1_array = calculate_eigenvalue_with_one_parameter(k_array, hamiltonian_1)
plot(k_array, E_1_array, xlabel='k', ylabel='E_1')
E_2_array = calculate_eigenvalue_with_one_parameter(k_array, hamiltonian_2)
plot(k_array, E_2_array, xlabel='k', ylabel='E_2')
# import guan
# E_1_array = guan.calculate_eigenvalue_with_one_parameter(k_array, hamiltonian_1)
# guan.plot(k_array, E_1_array, xlabel='k', ylabel='E_1')
# E_2_array = guan.calculate_eigenvalue_with_one_parameter(k_array, hamiltonian_2)
# guan.plot(k_array, E_2_array, xlabel='k', ylabel='E_2')
def calculate_eigenvalue_with_one_parameter(x_array, hamiltonian_function, print_show=0):
dim_x = np.array(x_array).shape[0]
i0 = 0
if np.array(hamiltonian_function(0)).shape==():
eigenvalue_array = np.zeros((dim_x, 1))
for x0 in x_array:
hamiltonian = hamiltonian_function(x0)
eigenvalue_array[i0, 0] = np.real(hamiltonian)
i0 += 1
else:
dim = np.array(hamiltonian_function(0)).shape[0]
eigenvalue_array = np.zeros((dim_x, dim))
for x0 in x_array:
if print_show==1:
print(x0)
hamiltonian = hamiltonian_function(x0)
eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
eigenvalue_array[i0, :] = eigenvalue
i0 += 1
return eigenvalue_array
def plot(x_array, y_array, xlabel='x', ylabel='y', title='', fontsize=20, labelsize=20, show=1, save=0, filename='a', file_format='.jpg', dpi=300, style='', y_min=None, y_max=None, linewidth=None, markersize=None, adjust_bottom=0.2, adjust_left=0.2):
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
plt.subplots_adjust(bottom=adjust_bottom, left=adjust_left)
ax.plot(x_array, y_array, style, linewidth=linewidth, markersize=markersize)
ax.grid()
ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman')
ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman')
if y_min!=None or y_max!=None:
if y_min==None:
y_min=min(y_array)
if y_max==None:
y_max=max(y_array)
ax.set_ylim(y_min, y_max)
ax.tick_params(labelsize=labelsize)
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontname('Times New Roman') for label in labels]
if save == 1:
plt.savefig(filename+file_format, dpi=dpi)
if show == 1:
plt.show()
plt.close('all')
if __name__ == '__main__':
main()计算结果:两个图相同。
四、在键长不同的情况下本征值等价证明
根据评论补充:当元胞内部的原子距离和元胞间距离不同时,即 a1 不等于 a2,此时两种方法的结果也是一样,前提是统一标准,例如间距 a1+a2=1。数值和解析均可以验证。解析推导要用到余弦公式 Cos(x+y)=CosxCosy-SinxSiny。以下是具体推导。
不妨令 a1+a2=1,哈密顿量的第一种形式:
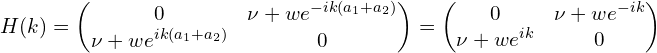
哈密顿量的第二种形式:
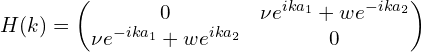
第一个形式和之前的相同,本征值也和之前的相同。
第二个形式的本征值为:
![Rendered by QuickLaTeX.com \begin{aligned}E_2&=\pm \sqrt{(v\cos (ka_1)+w\cos( ka_2))^2+ (v\sin(-ka_1)+w\sin( ka_2))^2}\\& =\pm \sqrt{(v+w)^2 +2vw\cos(ka_1)\cos(ka_2)-2vw\sin(ka_1)\sin(ka_2) }\\&=\pm \sqrt{ \nu^2+w^2+2\nu w \cos [k(a_1+a_2)] } \\&=\pm \sqrt{ \nu^2+w^2+2\nu w \cos k} \end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-0b5a5c78fba6517ffc7c3dae3e3b4a2b_l3.png)
本征值相同。
参考资料:
[1] 六角蜂窝格子紧束缚模型的计算
[2] WannierTools: An open-source software package for novel topological materials
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
老师,可以通过引入幺正变换U=[exp(-k a1/2) 0;0 exp(k a1/2)])将2种convention等效,即H1=U H2 U^dagger。因此2种方法的本征值肯定相同,而此幺正变换可以看作TB模型的基(不同原子在给定量子数k的Bloch波函数对应的产生/湮灭算符)的附加相位exp(±k a1/2)。这一点是不是会导致边界不连续性?
嗯,感谢你提出的这个理解视角。你说的这个我也不知道,你可以试着在解析上求解波函数,和原先的波函数进行对比,然后再考虑边界上的波函数情况。
老师,您好,最近我在学习如何计算一维SSH模型中的berry phase,但是当我哈密顿量选择以上不同的形式的时候,我发现计算出来的berry phase差了pi/2,在以原胞为单位的时候我发现计算的结果是对的,但是以原子时候是小了pi/2,这个如何去理解?还是我的计算是错了
我也不确定。你可以参考知乎这篇文章:六角蜂窝格子紧束缚模型的计算,里面提到了“在计算陈数时,如果波函数在布里渊区边界不连续,则需要额外考虑不连续性带来的积分贡献”。看是不是因为这个原因?
好的,谢谢老师
您好,我看到在您引用的参考资料[1]中有如下描述:“第一种FT规范下,因为H(k)≠H(k+G),所以求出来的波函数也没有周期性:ψ(k)≠ψ(k+G)。在计算陈数时,如果波函数在布里渊区边界不连续,则需要额外考虑不连续性带来的积分贡献。”
想请问您,如果要在此规范下求陈数或者Berry connection等,具体应该怎么处理?
嗯,这个问题挺好的,我之前都没怎么注意到这个。我感觉这个问题在严格的解析求解中会遇到,而在数值计算中有可能没太大影响(观点仅作参考),因为波函数本身就具有相位任意性,可以采用与波函数相位无关的算法来计算陈数或者Berry connection,可以参考:贝里曲率的计算(附Python代码)。六角格子的例子可以参考:Haldane模型中陈数的计算(附Python代码)。
感谢您的建议。我注意到一些模型在非布洛赫的哈密顿量下得到的波函数,其本身在布里渊区边界是不连续的(并非整体相位的影响),而您文中的“高效法”依然要求波函数在布里渊区边界是连续的。
然而如果在非布洛赫的规范下求(按照传统的公式)Wilson loop等参数时,能得到与布洛赫规范下不同的结果。所以我有以下猜想:1.非布洛赫规范下不能按照传统公式计算;2.两种结果都是对的,两种规范确实有不同的物理含义(甚至拓扑性)。如果是第一种猜想,正确的算法又应为何?
不知您能否解答我的疑惑。
嗯嗯,这个问题的相位好像跟普通相位(整体相位)是两回事,在数学上不等效。
第二个猜想肯定是不对的,两种规范不可能具有不同的物理含义。
第一个猜想我还不确定,数值计算上目前好像没有遇到问题(Haldane模型中陈数的计算(附Python代码))。如果遇到结果不对,可以把非布洛赫的规范的波函数改成布洛赫的规范的波函数,然后再继续算。如果一定要用非布洛赫的规范的波函数,计算结果有可能会有个偏差,至于偏差多少需要解析上进行推导和分析吧。
好的,非常感谢。
你好,对于胞内和胞外间距不同时的·傅里叶变换有参考资料吗
方法和上面是一样的呀,把两个1/2分别用a1和a2来代替,同样再算一下,结果是一样的,不需要其他参考资料了。
已更新这种情况的具体推导过程。
您好,假如元胞内部的原子距离和元胞间距离不同时是不是只能选用第二种方法?
即使a1不等于a2时,两种方法的结果也是一样,前提是统一标准,例如间距a1+a2=1。我数值和解析都验证过了,没问题的。
解析推导要用到余弦公式cos(x+y)= cos(x)cos(y)-sin(x)sin(y)。
已更新这种情况的具体推导过程。