石墨烯在各个高对称轴上的能带结构（附Python代码）

这是之前的一篇：石墨烯哈密顿量与能带图（附Python代码）。

本篇画出石墨烯在各个高对称轴上的能带结构，有K-Gamma轴、Gamma-M轴、M-K轴。

石墨烯在实空间中原子坐标示意图：

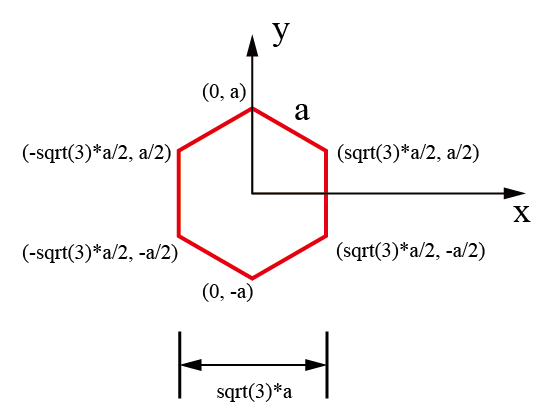
石墨烯在倒空间中高对称轴示意图：

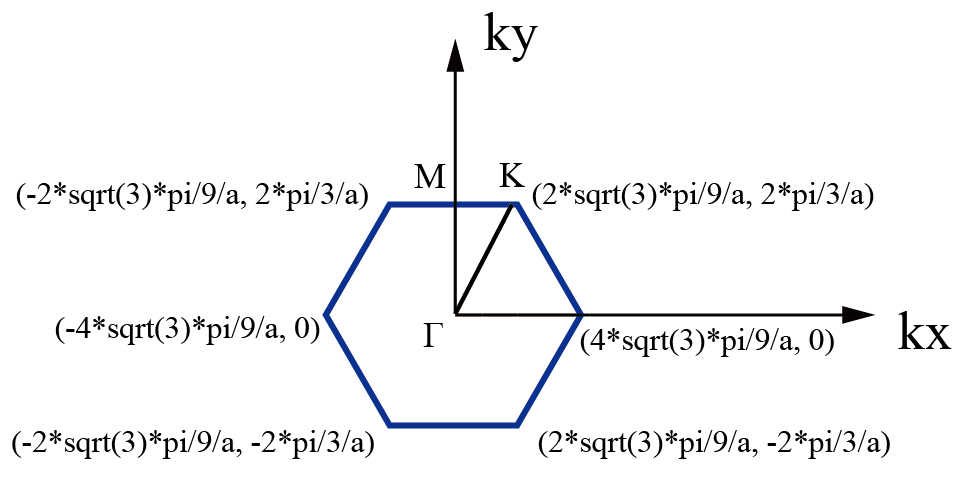
倒格子的坐标可参考：倒格子基矢的计算（附数值计算、符号计算Python代码）。

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6260
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入sqrt(), exp(), pi等
import cmath  # 要处理复数情况，用到cmath.exp()


def hamiltonian(k1, k2, M=0, t1=1, a=1/sqrt(3)):  # Haldane哈密顿量(a为原子间距，不赋值的话默认为1/sqrt(3)）
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    # 质量项(mass term), 用于打开带隙
    h0[0, 0] = M
    h0[1, 1] = -M

    # 最近邻项
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[1, 0].conj()

    # # 最近邻项也可写成这种形式
    # h1[1, 0] = t1+t1*cmath.exp(1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)+t1*cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)
    # h1[0, 1] = h1[1, 0].conj()

    matrix = h0 + h1
    return matrix


def main():
    a = 1/sqrt(3)
    Gamma0 = np.array([0, 0])
    M0 = np.array([0, 2*pi/3/a])
    K0 = np.array([2*np.sqrt(3)*pi/9/a, 2*pi/3/a])

    kn = 100  # 每个区域的取点数
    n = 3  # n个区域（K-Gamma，Gamma-M, M-K）
    k1_array = np.zeros(kn*n) 
    k2_array = np.zeros(kn*n)

    # K-Gamma轴
    k1_array[0:kn] = np.linspace(0, K0[0], kn)[::-1] # [::-1]表示反转数组
    k2_array[0:kn] = np.linspace(0, K0[1], kn)[::-1]

    # Gamma-M轴
    k1_array[kn:2*kn] = np.zeros(kn)
    k2_array[kn:2*kn] = np.linspace(0, M0[1], kn)

    # M-K轴
    k1_array[2*kn:3*kn] = np.linspace(0, K0[0], kn)
    k2_array[2*kn:3*kn] = np.ones(kn)*M0[1]
    
    i0 = 0
    dim = hamiltonian(0, 0).shape[0]
    eigenvalue_k = np.zeros((kn*n, dim))
    fig, ax = plt.subplots() 
    for kn0 in range(kn*n):
        k1 =  k1_array[kn0]
        k2 =  k2_array[kn0]
        eigenvalue, eigenvector = np.linalg.eig(hamiltonian(k1, k2))
        eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
        i0 += 1
    for dim0 in range(dim):
        plt.plot(range(kn*n), eigenvalue_k[:, dim0], '-k') 
    plt.ylabel('E')
    ax.set_xticks([0, kn, 2*kn, 3*kn])
    ax.set_xticklabels(['K', 'Gamma', 'M', 'K'])
    plt.xlim(0, n*kn)
    plt.grid(axis='x',c='r',linestyle='--')
    plt.show()


if __name__ == '__main__':
    main()

计算结果为：

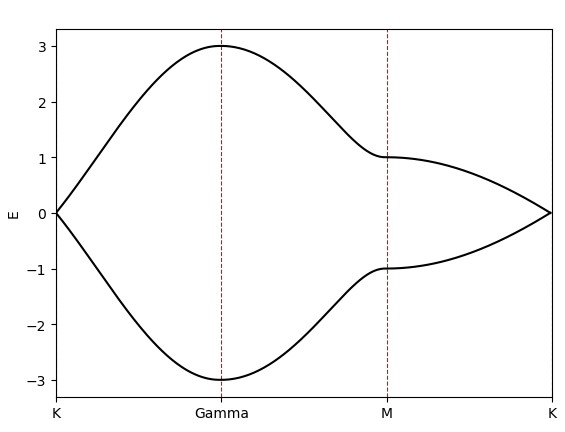
参考资料：

[1] 石墨烯的晶格和能带结构

6,877 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】