这是之前的一篇：空间反演对称性破缺的石墨烯的贝里曲率分布（附Python代码），因为用到定义公式，需要对波函数求导，所以在计算时通常要寻找固定的规范，使得不同k点的波函数具有连续性。
本篇将分别用以下这三篇中的方法计算贝里曲率（本篇程序没有最后的求和）：
- 陈数Chern number的计算（高效法，附Python/Matlab代码）
- 陈数Chern number的计算（Wilson loop方法，附Python代码）
- 陈数Chern number的计算（Kubo公式，附Python代码）
用到的哈密顿量例子同样是空间反演对称性破缺的石墨烯。计算结果和这篇相同：空间反演对称性破缺的石墨烯的贝里曲率分布（附Python代码）。
如果需要代码写成函数的形式，可以阅读：贝里曲率的计算（写成函数形式，附Python代码）。
一、贝里曲率高效法
这个方法的最后需要除以delta*delta的面积，参考[1]：
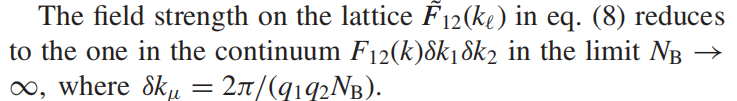
根据贝里曲率的定义，还需要额外乘一个虚数才可以得到贝里曲率。
Python代码如下：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/20869
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
def hamiltonian(k1, k2, t1=2.82, a=1/sqrt(3)): # 石墨烯哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
h = np.zeros((2, 2), dtype=complex)
h[0, 0] = 0.28/2
h[1, 1] = -0.28/2
h[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h[0, 1] = h[1, 0].conj()
return h
def main():
n = 2000 # 取点密度
delta = 4*pi/n # 求导的偏离量
for band in range(2):
F_all = [] # 贝里曲率
for kx in np.linspace(-2*pi, 2*pi, n):
for ky in [0]: # 这里只考虑ky=0对称轴上的情况
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 价带波函数
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx的波函数
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离ky的波函数
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx和ky的波函数
Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))
F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))/delta/delta*1j
F_all = np.append(F_all,[F], axis=0)
plt.plot(np.linspace(-2*pi, 2*pi, n)/pi, np.real(F_all))
plt.xlabel('k_x (pi)')
plt.ylabel('Berry curvature')
if band==0:
plt.title('Valence Band')
else:
plt.title('Conductance Band')
plt.show()
if __name__ == '__main__':
main()二、贝里曲率Wilson loop方法
Wilson loop方法和高效法在表达式上其实差别不大：在Wilson loop方法中没有除以模，但需要对路径上的点多次乘积。
Python代码如下：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/20869
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
def hamiltonian(k1, k2, t1=2.82, a=1/sqrt(3)): # 石墨烯哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
h = np.zeros((2, 2), dtype=complex)
h[0, 0] = 0.28/2
h[1, 1] = -0.28/2
h[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h[0, 1] = h[1, 0].conj()
return h
def main():
n1 = 1000 # small plaquettes精度
n2 = 10 # Wilson loop精度
delta = 2*pi/n1
for band in range(2):
F_all = [] # 贝里曲率
for kx in np.linspace(-2*pi, 2*pi, n1):
for ky in [0]: # 这里只考虑ky=0对称轴上的情况
vector_array = []
# line_1
for i2 in range(n2+1):
H_delta = hamiltonian(kx+delta/n2*i2, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta)
vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))[band]]
vector_array.append(vector_delta)
# line_2
for i2 in range(n2):
H_delta = hamiltonian(kx+delta, ky+delta/n2*(i2+1))
eigenvalue, eigenvector = np.linalg.eig(H_delta)
vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))[band]]
vector_array.append(vector_delta)
# line_3
for i2 in range(n2):
H_delta = hamiltonian(kx+delta-delta/n2*(i2+1), ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta)
vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))[band]]
vector_array.append(vector_delta)
# line_4
for i2 in range(n2-1):
H_delta = hamiltonian(kx, ky+delta-delta/n2*(i2+1))
eigenvalue, eigenvector = np.linalg.eig(H_delta)
vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))[band]]
vector_array.append(vector_delta)
Wilson_loop = 1
for i0 in range(len(vector_array)-1):
Wilson_loop = Wilson_loop*np.dot(vector_array[i0].transpose().conj(), vector_array[i0+1])
Wilson_loop = Wilson_loop*np.dot(vector_array[len(vector_array)-1].transpose().conj(), vector_array[0])
arg = np.log(Wilson_loop)/delta/delta*1j
F_all = np.append(F_all,[arg], axis=0)
plt.plot(np.linspace(-2*pi, 2*pi, n1)/pi, np.real(F_all))
plt.xlabel('k_x (pi)')
plt.ylabel('Berry curvature')
if band==0:
plt.title('Valence Band')
else:
plt.title('Conductance Band')
plt.show()
if __name__ == '__main__':
main()三、贝里曲率Kubo公式
这里按理说需要对所有其他能带求和，但因为考虑的是两带系统，所以没有求和的过程。
Python代码如下：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/20869
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
def hamiltonian(k1, k2, t1=2.82, a=1/sqrt(3)): # 石墨烯哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
h = np.zeros((2, 2), dtype=complex)
h[0, 0] = 0.28/2
h[1, 1] = -0.28/2
h[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h[0, 1] = h[1, 0].conj()
return h
def main():
n = 2000 # 取点密度
delta = 1e-9 # 求导的偏离量
for band in range(2):
F_all = [] # 贝里曲率
for kx in np.linspace(-2*pi, 2*pi, n):
for ky in [0]: # 这里只考虑ky=0对称轴上的情况
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
if band==0:
vector_0 = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]
vector_1 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]
elif band==1:
vector_0 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]
vector_1 = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]
eigenvalue = np.sort(np.real(eigenvalue))
H_delta_kx = hamiltonian(kx+delta, ky)-hamiltonian(kx, ky)
H_delta_ky = hamiltonian(kx, ky+delta)-hamiltonian(kx, ky)
berry_curvature = 1j*(np.dot(np.dot(np.dot(np.dot(np.dot(vector_0.transpose().conj(), H_delta_kx/delta), vector_1), vector_1.transpose().conj()), H_delta_ky/delta), vector_0)- np.dot(np.dot(np.dot(np.dot(np.dot(vector_0.transpose().conj(), H_delta_ky/delta), vector_1), vector_1.transpose().conj()), H_delta_kx/delta), vector_0))/(eigenvalue[0]-eigenvalue[1])**2
F_all = np.append(F_all,[berry_curvature], axis=0)
plt.plot(np.linspace(-2*pi, 2*pi, n)/pi, np.real(F_all))
plt.xlabel('k_x (pi)')
plt.ylabel('Berry curvature')
if band==0:
plt.title('Valence Band')
else:
plt.title('Conductance Band')
plt.show()
if __name__ == '__main__':
main()参考文献：
[1] Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
guan老师，我没有学过python，但是根据其他语言多少可以看得懂您的程序，我想请问一下哈密顿量里面的k1和k2代表什么？
动量k_x或k_y。因为不同地方x和y方向的定义不一样，容易搞混，所以我这里用k1和k2代替，可以是kx和ky，也可以是ky和kx。
好的，谢谢关老师的回复
您好，我能理解其中的Wilson loop方法，但无法理解高效法，您说两者比较相似，能不能请您解释一下后者？
公式上是很接近的，差别只在是否除以它们内积的模。
您好，请问一下在Wilson loop方法中，对于每一个kx计算arg时，公式arg=np.log(Wilson_loop)/delta/delta*1j中为什么除了两个delta呢？
贝里相位和贝里曲率的关系，有一个面积分。参考：贝里相位、贝里联络、贝里曲率和陈数。
你好，计算小白，我想问如何构造其他物质的哈密顿量？要知道什么参数
一般是要从第一性原理计算出发，通过近似或者群论化简，得到维度相对比较低的紧束缚哈密顿量或KP哈密顿量，以及对应的参数。