在线留言

目录
1. 本站留言说明
2. 所有最近留言
3. 当前页面留言

1. 本站留言说明

（1）在保留浏览器缓存的前提下，本站评论支持72小时自主修改或删除个人评论。如果自己无法修改或删除评论，可再次评论或联系我。如有发现广告留言，请勿点击链接，博主会不定期删除。

（2）本站评论支持Latex公式。把latexpage作为标签放在任何位置，评论中的公式可正常编译，示例：

[latexpage] $Latex formula$

（3）本站评论支持代码格式。在代码前后加上以下标签，留言可保留缩进显示代码：

<!-- wp:code --><pre class="wp-block-code"><code>
	代码内容
</code></pre><!-- /wp:code -->

2. 所有最近留言

这里显示本站的所有文章和页面中的最近 100 条留言。

  1. 头像

    找出对应的元胞，写出哈密顿量，然后按照公式定义计算就行了。倒空间的哈密顿量可以参考：离散格子的傅里叶变换和反傅里叶变换、以SSH模型为例子说明两种傅里叶变换方法。

  2. 头像
  3. 头像

    嗯，是的，我稍微看了下AI生成的回答，推导好像没太大问题。另外，可以参考：时间和空间反演操作对位置、动量、角动量的作用。 我个人觉得是这样的，但不能百分百给你保证。如果还不放心，可以找一些教材或者搜一些文献看看，再确认下。

  4. 头像
  5. 头像

    时间反演和空间反演对 $e^{i\mathbf{k}\cdot\mathbf{r}}$ 也有作用，包括复数共轭、k取负，或者r取负。 以下是 GPT-4o 的回答，供参考： 在同时满足时间反演和空间反演对称的周期性系统中，布洛赫波函数具有特殊的对称性。具体来说，布洛赫波函数 $\psi_{\mathbf{k}}(\mathbf{r})$ 在这些对称性的作用下，会满足一些对称关系。 1. 时间反演对称性：时间反演对称性要求系统在时间反演操作下不变。时间反演操作会将动量 $\mathbf{k}$ 变为 $-\mathbf{k}$，并且还会将波函数复共轭。因此，对于时间反演对称性，我们有： $ \psi_{\mathbf{k}}(\mathbf{r}) = \mathcal{T} \psi_{\mathbf{k}}(\mathbf{r}) = \psi^*_{-\mathbf{k}}(\mathbf{r}) $ 其中 $\mathcal{T}$ 表示时间反演操作。 2. 空间反演对称性：空间反演对称性要求系统在空间反演操作下不变。空间反演操作会将位置 $\mathbf{r}$ 变为 $-\mathbf{r}$，并且会改变动量的方向。因此，对于空间反演对称性，我们有： $ \psi_{\mathbf{k}}(\mathbf{r}) = \mathcal{P} \psi_{\mathbf{k}}(\mathbf{r}) = \psi_{-\mathbf{k}}(-\mathbf{r}) $ 其中 $\mathcal{P}$ 表示空间反演操作。 在一个同时满足这两种对称性的系统中，布洛赫波函数需要同时满足这两种对称性。结合这两种对称性，可以得到以下关系： 3. 结合时间反演和空间反演对称性：通过结合这两种对称性，可以得到： $ \psi_{\mathbf{k}}(\mathbf{r}) = \psi^*_{-\mathbf{k}}(\mathbf{r}) = \psi^*_{\mathbf{k}}(-\mathbf{r}) $ 这意味着布洛赫波函数在复共轭和空间反演操作下保持不变。 此外，对于布洛赫波函数的一般形式 \(\psi_{\mathbf{k}}(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}} u_{\mathbf{k}}(\mathbf{r})\)，其中 \(u_{\mathbf{k}}(\mathbf{r})\) 是周期函数，也可以推导出相应的对称性： 时间反演对称性要求： \[ u_{\mathbf{k}}(\mathbf{r}) = u^*_{-\mathbf{k}}(\mathbf{r}) \] 空间反演对称性要求： \[ u_{\mathbf{k}}(\mathbf{r}) = u_{-\mathbf{k}}(-\mathbf{r}) \] 结合这两种对称性，可以进一步得到 \(u_{\mathbf{k}}(\mathbf{r})\) 在复共轭和空间反演下的不变性。 [latexpage]

  6. 头像

    同时满足时间反演、空间反演对称的周期性系统，u(-k)=u(k), u(-k)=u*(k), 那么u(k)=u*(k)，也就是说u(k)是处处为实数的场。可是对于特定的k，周期性边界条件要求u(k)_1=u(k)_0*exp(i k r)，因为exp(i k r)带虚部，就没法保证两个边界点的值u(k)_1, u(k)_0是实数了，这也就和u(k)处处为实数冲突了。想不明白这是怎么回事。

  7. 头像

    我目前没具体算过，但应该还是按定义公式来算，哈密顿量还是需要满足手性这个条件，只是这时候h(k)是一个矩阵。处理方法有可能是对h(k)求本征值，分成两条带分别进行计算，这是我的猜想，不一定对，供参考，你可以查查文献有没有提供四带的结果，计算验证一下。

  8. 头像
  9. 头像
  10. 头像
  11. 头像

    关老师，我按照您这个Nested Wilson loop写了这个BBH模型在半开边界条件下的边界极化。按照公式的定义写出来但是算的不对。能麻烦您帮我看一下吗？算了快一周不知道哪里写的有问题。 clc; clear; t=0.0; gamma_x=0.5; gamma_y=0.5; lambda=1; Ly=20; num_k=50; N_orb=4;%Ly 元胞数 N=num_k; N_occ=2; rho_j=zeros(Ly,1); kx1=linspace(-pi,pi,num_k); kx3=-1*pi; W=Wilson_loop(kx3,gamma_x,gamma_y,lambda,t,Ly); %求解Wilson loop [nu_kx,E1]=eig(-1i*logm(W)); % wannier hamiltonian [B,I]=sort(real(diag(E1))); nu_j=sort((real(diag(E1)))/(2*pi)); % nu_j 按照能量实部排序 [V,~]=eig(W); for i=1:length(I) nu_kx1(:,i)=nu_kx(:,I(i)); % Wilson loop 的本征态 end for i=1:length(kx1) kx=kx1(i); H=[]; rho_j=zeros(Ly,1); H=H_3(kx,gamma_x,gamma_y,lambda,t,Ly); [V,~]=eig(H); u_kx=V(:,1:end/2); for j=1:N_occ*Ly for n=1:N_occ*Ly for ialpha=1:N_orb % sum alpha for iy=1:Ly rho_j(iy)=rho_j(iy)+abs(u_kx((iy-1)*N_orb+ialpha,n)... *nu_kx1(n,j)).^2*nu_j(j); end end end end rho_j1(:,i)=rho_j; end rho_j=sum(rho_j1,2); rho=rho_j/N; sum(rho(1:10)) Ry=[1:Ly]; plot(Ry,rho,'bo-'); xlabel('R_y'); ylabel('p_x'); function H_total=H_3(kx,gamma_x,gamma_y,lambda,t,Ly) %Ly 元胞数 H_0=[zeros(2) [lambda*exp(1i*kx)+gamma_x gamma_y;-gamma_y gamma_x+lambda*exp(-1i*kx)];... [lambda*exp(-1i*kx)+gamma_x -gamma_y; gamma_y gamma_x+lambda*exp(1i*kx)] zeros(2)]; delta=1e-4; % delta=1e-4 引入微扰消除简并 H_0=H_0+eye(4)*2*t*cos(kx)+diag([-delta -delta delta delta]); H_1=zeros(4); H_1(1,4)=lambda; H_1(3,2)=-lambda; H_1=H_1+eye(4)*t; H_total=kron(eye(Ly),H_0)+kron(diag(ones(Ly-1,1),1),H_1)+kron(diag(ones(Ly-1,1),-1),H_1'); % ' .' 区别 end % large Wilson loop function W=Wilson_loop(kx,gamma_x,gamma_y,lambda,t,Ly) vector=[]; num_k=51; kx1=linspace(kx,kx+2*pi,num_k); for i=1:length(kx1) kx=kx1(i); H=H_3(kx,gamma_x,gamma_y,lambda,t,Ly); Size_W=size(H,1)/2; [V,~]=eig(H); if kx~=kx1(end) % kx+2*pi 多个威尔逊环 for ii=1:Size_W vector(:,ii,i)=V(:,ii); end else vector(:,:,i)=vector(:,:,1); end end W1=eye(Size_W); for i=1:length(kx1)-1 F=zeros(Size_W,Size_W,length(kx1)); for m=1:size(vector,2) for n=1:size(vector,2) F(m,n,i)=dot(vector(:,m,i+1),vector(:,n,i)); end end W1=F(:,:,i)*W1; end W=W1; end 参考文献

  12. 头像

    做得不错，在上面学到了很多，谢谢大佬

  13. 头像
  14. 头像

    请问如果在两层之间加水平磁场，方格子怎么加啊那个z方向的积分体现在哪一项啊

  15. 头像
  16. 头像
  17. 头像
  18. 头像
  19. 头像
  20. 头像
  21. 头像

    这个我也不清楚，没法回答你的问题。按理来说，得到0的本征向量不是物理的结果，甚至不是数学的结果，本征向量不应该为0的。可以检查下公式，看投影的过程是否是对的，或者可能本身是不存在解。另外，对于简并的情况，波函数可能需要正交归一化处理一下。

  22. 头像

    非常感谢您，我其实是在用Wilson Loop (简并能带) 情况计算自旋陈数，在高对称点会有单纯自旋向上或向下的情况，如果这个时候用自旋投影算符，就会得到为0的本征向量，请问这种情况应该怎么处理呢？

  23. 头像
  24. 头像
  25. 头像
  26. 头像
  27. 头像
  28. 头像

    老师，在计算嵌套威尔逊环时，体系的哈密顿量为什么要这样写，为什么和计算能带和威尔逊环时写法不一样?另外，文章计算（Benalcazar, Bernevig, Hughes, Science 357,61–66 (2017)）极化P_y_vx，公式显示对kx求和或者是积分，而您的代码中在哪里体现这个求和？ def hamiltonian(kx, ky): # BBH model # label of atoms in a unit cell # (2) —— (0) # | | # (1) —— (3) gamma_x = 0.5 # hopping inside one unit cell lambda_x = 1 # hopping between unit cells gamma_y = gamma_x lambda_y = lambda_x x_symmetry_breaking_1 = 0.000000000000 # default (not breaking): zero x_symmetry_breaking_2 = 1.0000000000001 # default (not breaking): unity y_symmetry_breaking_1 = 0.000000000000 # default (not breaking): zero y_symmetry_breaking_2 = 1.000000000000 # default (not breaking): unity h = np.zeros((4, 4), dtype=complex) h[0, 0] = x_symmetry_breaking_1 h[1, 1] = y_symmetry_breaking_1 h[2, 2] = y_symmetry_breaking_1 h[3, 3] = x_symmetry_breaking_1 h[0, 2] = (gamma_x+lambda_x*cmath.exp(1j*kx))*y_symmetry_breaking_2 h[1, 3] = gamma_x+lambda_x*cmath.exp(-1j*kx) h[0, 3] = gamma_y+lambda_y*cmath.exp(1j*ky) h[1, 2] = (-gamma_y-lambda_y*cmath.exp(-1j*ky))*x_symmetry_breaking_2 h[2, 0] = np.conj(h[0, 2]) h[3, 1] = np.conj(h[1, 3]) h[3, 0] = np.conj(h[0, 3]) h[2, 1] = np.conj(h[1, 2]) return h

  29. 头像

    缠绕数（winding number）通常是需要定义在手征对称的系统中， 而 Wilson loop 可以定义在任意的闭合路径上。它们不是完全等价的。 但在具有手征对称性的系统中，它们可以传达相似的拓扑信息。我个人的理解是它们是一致的，但我没详细证明过，这篇文献 “Connection between the winding number and the Chern number [https://doi.org/10.1016/j.cjph.2020.12.025]” 有给出卷绕数和陈数的关系，我还没详细看过，供参考。另外，陈数和 poralization/Wilson loop 也是有关系的，所以对于手征对称的系统，卷绕数和 Wilson loop 有一定的对应关系。 可能还有其他的文献中也讨论过这个问题，例如：这篇文献 “Band topology in classical waves: Wilson-loop approachto topological numbers andfragile topology [https://doi.org/10.1088/1367-2630/ab3f71]” ，以及这个讲义 “Lecture notes on Berry phases and topology [https://scipost.org/SciPostPhysLectNotes.51]”。更多文献可以自己搜一下。

  30. 头像

    请问，SSH模型中缠绕数和wilson loop都是拓扑不变量，它们之间有什么关系？手征对称的系统的缠绕数和wilson loop都是等价的吗？

  31. 头像
  32. 头像

    关老师您好，非常感谢您的代码！我在用Wilson Loop 方法计算Chern number 时，出现了在一些高对称点得到本征向量为0的情况，请问应该怎么处理呢？我看到您标注了一些参考资料，但是没有从其中找到处理方法。

  33. 头像

    谢谢guan老师回答,我也是小白,这个软件提供eigenvalue加eigenvector的信息,但是这个文件好像是二进制的.....

  34. 头像

    非常感謝您的回覆，這個model是參考了"a short course on topological insulators"的內容。我有重新讀了一下關於這個model的內容，文章中透過解析解的方式有給出了陳數與u的關係，我推測會跑出-0.5是因為當我選取的u=2時剛好落在 0<u2 此時可能只包到了半個參考點。 我有測試過符合區間內的u，結果都符合解析出來的預期。

  35. 头像

    嗯，数学上可能会有复数的情况，这个我不大了解。在物理上，波函数相邻k点一般是连续的，以及波函数需要归一化（量子力学的基本性质），所以贝里曲率为实数。其实也比较好理解，因为贝里曲率是倒空间的“磁场”，如果为复数会有点奇怪，另外，它在布里渊区的积分也要为整数。 你说的向量长度应该没什么关系，即使不是1，是其他长度，求导也是0，同样有一样的证明结果。

  36. 头像

    感谢！也就是说贝利曲率虚部为0的条件是本征向量丛是个每个向量都归一化的复向量丛，如果本征向量在参数空间中长度分布不一致，就产生了贝利联络的非零虚部，但那是没意义的（本征向量乘任意常数还是它本身）。这样理解正确吧？

  37. 头像
  38. 头像

    我目前没用过这个软件，不大熟悉。如果要计算Berry Curv，需要系统的波函数信息，而不是能带，看这个软件是否有提供波函数，然后按照公式计算就行了。

  39. 头像

    老师您好。我得到一个能带在二维布里渊区中的本征向量丛，用文中的公式导出贝利曲率在布里渊区上的分布，它虚部并不是零，反而比实部还大一些（在您给我们展示的石墨烯的例子中，它的虚部是接近0的，只有一点数值误差）。因此我想知道“贝利曲率是实数”是怎么来的，如果用文中的公式导出的贝利曲率实部虚部都不接近零，这个虚部的物理意义是什么？

  40. 头像

    guan老师您好,我通过wien2k进行了scf计算,之后用xcrysden选择了自己想要的kpath算出了E(k)能带图,想用Kubo公式进行Berry Curv计算,不太清楚老师的这个代码该怎么用呢?

  41. 头像
  42. 头像

    我问了GPT，这样修改好像就可以了（具体哪里出错，可以自己检查下，我也没仔细看）： 这个 [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) ) ) ; 修改成 [~, ind] = sort(diag(D)); % Sort eigenvalues V = V(:, ind); % Sort eigenvectors accordingly 另外你这个模型运行结果是 -0.5，我不知道是什么原因。如果改成博文中的模型，结果是 -2，好像没什么问题。 H(1,2)=2*cos(kx(nkx))-1i*2*cos(ky(nky)); H(2,1)=2*cos(kx(nkx))+1i*2*cos(ky(nky)); H(1,1)=-1+2*0.5*sin(kx(nkx))+2*0.5*sin(ky(nky))+2*cos(kx(nkx)+ky(nky)); H(2,2)=-(-1+2*0.5*sin(kx(nkx))+2*0.5*sin(ky(nky))+2*cos(kx(nkx)+ky(nky)));

  43. 头像

    謝謝您的回覆，上述的代碼我少附了定義布里渊区范围的參數。 重新附上一份完整的內容，關於上述您提到我可以檢查的方式我目前都有檢查過。 我有試著使用您的程式碼來測試我的哈密頓量所計算出的陳數，似乎是沒有問題的。 我認為到給出哈密頓量的部分都沒有問題，我也有解出能譜結構是沒問題的。問題似乎是出現在後續給解出本徵相量Ｖ和做循環內積時，不知道是否我有哪個地方的邏輯不太正確。 clc clear all close all Nk = 1000; kx = linspace( -pi , pi , Nk ); ky = kx; u = 2 ; H = zeros( 2 , 2 ); sigmax = [ 0 , 1 ; 1 , 0 ]; sigmay = [ 0 , -i ; i , 0 ]; sigmaz = [ 1 , 0 ; 0 , -1 ]; for nkx = 1 : Nk for nky = 1 : Nk H = sin(kx(nkx)) * sigmax + sin(ky(nky)) * sigmay +( u + cos(kx(nkx)) + cos(ky(nky)) ) * sigmaz; [ V , D ] = eig(H); [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) ) ) ; ES1( nkx , nky , : ) = V( : , ind(1) ) ; end end Nk2 = zeros( Nk-1 , Nk-1); for nx = 1:Nk-1 for ny = 1:Nk-1 M1 = sum ( conj( ES1( nx , ny , 🙂 ) .* ES1( nx+1 , ny , : ) ,3 ) ; M2 = sum ( conj( ES1( nx+1 , ny , 🙂 ) .* ES1( nx+1 , ny+1 , : ) ,3 ); M3 = sum ( conj( ES1( nx+1 , ny+1 , 🙂 ) .* ES1( nx , ny+1 , : ) ,3 ); M4 = sum ( conj( ES1( nx , ny+1 , 🙂 ) .* ES1( nx , ny , : ) , 3 ); M = M1 * M2 * M3 * M4 ; CV = -imag( log (M) ) ; Nk2( nx , ny ) = CV ; end end %[ kkx , kky ] = meshgrid( kx(1:Nk-1) , ky(1:Nk-1) ) ; surfc ( Nk2 ) ; % shading interp X = Nk2(:) ; % n x n brillouin zone -> 1D ex: [1,2,;3,4]->[1,2,3,4] Y = sum(X); Z=sum(X)/2/pi; % chern number set(gca,'xticklabel',[]); set(gca,'yticklabel',[]);

  44. 头像

    这个代码好像缺少一些变量，没法直接运行。我一时也没法马上看出来，你可以检查下：（1）检查这个哈密顿量的布里渊区范围，这决定了积分的范围。（2）检查这个能带是否有交叉或简并的情况，如果有简并，可以参考这篇：陈数Chern number的计算（多条能带的高效法，附Python代码）。（3）还有一个简单的检查方法是：你把哈密顿量换成博文中的例子，看结果是否正确，用来验证其他代码是不是对的，如果不对，可以把Nk取很小，然后一步步看具体的数值差异在哪里。

  45. 头像

    您好，我參考了您的文章 寫了一個程式計算QWZ model , 我的做法是直接用for loop 變動及儲存 每個kx , ky 的值 最後做循環內積，但結果一直不太正確 ， 不知道能不能請教您具體的問題可能出在哪裡。 u = 2 ; H = zeros( 2 , 2 ); sigmax = [ 0 , 1 ; 1 , 0 ]; sigmay = [ 0 , -i ; i , 0 ]; sigmaz = [ 1 , 0 ; 0 , -1 ]; for nkx = 1 : Nk for nky = 1 : Nk H = sin(kx(nkx)) * sigmax + sin(ky(nky)) * sigmay +( u + cos(kx(nkx)) + cos(ky(nky)) ) * sigmaz; [ V , D ] = eig(H); [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) ) ) ; ES( nkx , nky , : ) = V( : , ind(1) ) ; end end Nk2 = zeros( Nk-1 , Nk-1); for nx = 1:Nk-1 for ny = 1:Nk-1 M1 = sum ( conj( ES( nx , ny , 🙂 ) .* ES1( nx+1 , ny , : ) ,3 ) ; M2 = sum ( conj( ES( nx+1 , ny , 🙂 ) .* ES1( nx+1 , ny+1 , : ) ,3 ); M3 = sum ( conj( ES( nx+1 , ny+1 , 🙂 ) .* ES1( nx , ny+1 , : ) ,3 ); M4 = sum ( conj( ES( nx , ny+1 , 🙂 ) .* ES1( nx , ny , : ) , 3 ); M = M1 * M2 * M3 * M4 ; CV = -imag( log (M) ) ; Nk2( nx , ny ) = CV ; end end X = Nk2(:) ; Y = sum(X); Z=sum(X)/2/pi; % chern number set(gca,'xticklabel',[]); set(gca,'yticklabel',[]);

  46. 头像

    嗯，“独立”不同场景下定义不一样，文字表述有点差异，不是很重要，只要意思理解了就行。另外，“统计”的近似严格来说应该是“多体相互作用”的近似，因为统计包含了单体的统计，这里强调的是对多体问题的处理。

  47. 头像

    我们老师提到是因为pauli不相容所以看成相对的独立。我一开始笔记里漏了相对的这个单词，正好刚刚重新看了其他老师的笔记里是有这个单词的。我个人理解这是一种基于统计学情况的近似处理。一家之言，欢迎指正。

  48. 头像
  49. 头像

    关老师您好，请问zak相位是不是只能针对unit cell 的一条能带去计算，因为我看zak相的计算涉及到对布里渊区的积分。如果我的系统是有缺陷的，只有左右是周期性的，上下边界则用的是散射边条或者完美电导体边界条件，那这种情况还能计算单元结构能带的zak相吗？

  50. 头像

    如果是量子点，直接写出其对应的实空间哈密顿量，对角化后的本征态就是能级。至于哪个能级是边缘态，需要看波函数的模方分布。 如果形状顺序不是有规律的，需要固定好编号，然后再写哈密顿量，参考：方格子模型在实空间中的哈密顿量形式。

  51. 头像
  52. 头像
  53. 头像
  54. 头像
  55. 头像

    挺好的一个问题，我之前也发现了这个现象，其实也不是完全懂，但大概率就是由于晶格离散化所导致的，因为二维电子气的朗道能级不存在震荡的现象，参考：二维电子气的朗道能级。 以下是我个人的理解，不一定对，供参考。 （1）二维电子气晶格化后k^2对应的是cos的形式，这个近似应该是在k=0附近才比较成立，然而方格子的k=0时不是最低能量，因此当费米能E=0时，晶格化后的朗道能级和二维电子气的朗道能级会呈现出一些偏差。至于震荡的来源，应该是由于晶格周期性和有限尺寸的影响。 （2）对于六角格子，它的低能部分E=0附近刚好是线性的，满足狄拉克费米子的性质，参考：狄拉克电子朗道能级的根号N分布，因此在晶格中朗道能级的数值计算的结果和理论值比较吻合。

  56. 头像

    您好，我想请问一下，这里的六角格子算出来的LLs都是平的，并且不同的k对应相同的E，我的问题是你这里写的程序应该是周期性条件下的，对吧，不是开边界的条件；还有就是我也看了您写的方格子的LLs，为什么方格子的LLs在E=0附近就是低能部分是关于cos振荡的，而不是想六角格子一样都是平。

  57. 头像

    如果把kz作为参数，kx和ky作为维度，那么是可以看做是包含kz参数的二维哈密顿量，但这个形式和三维哈密顿量是一样的。 如果把kx和ky反傅里叶变换到实空间，x和y方向取有限宽度，然后保留kz，那么是准一维的哈密顿量（tube），沿着z方向。

  58. 头像

    老师您好，如果想要处理一个包含kx,ky,kz的三维动量空间哈密顿量，将其利用傅里叶变换转到实空间，在此过程中是否可以将kz看作体系参数保留k空间的形式，从而把三维哈密顿量等效为二维有效哈密顿量

  59. 头像
  60. 头像
  61. 头像
  62. 头像

    这个可能和模型的参数或相位有关。或者是跟跃迁强度t的正负号有关，这直接决定了能带是否上下颠倒。 对于给定的哈密顿量，如果计算出来的陈数结果都是刚好正负号相反，那么结果应该是没问题。如果是有的正，有的负，这个还不好说，可以检查下价带的总陈数的符号是否保持稳定，如果总陈数的符号不稳定，那么结果就是有问题，这是因为对于确定的体系，手性边缘态的方向是固定的。

  63. 头像

    关教授您好，我最近复现了这篇https://iopscience.iop.org/article/10.1088/0953-8984/27/4/045601/pdf关于量子反常霍尔QAH模型，这篇文章中的哈密顿量和您参考文献中的哈密顿量明明是一样的，为什么相图中陈数的数值会相差一个负号呀。我在计算bott index的过程中发现我的相图在一些区域还是有正负号的差别，难道说这个正负号不影响计算结果？ 这个问题困扰我蛮久，期待您的回复，谢谢您。

  64. 头像

    有了解一些，但目前没详细做过计算，好像可以从Polarization、Bott index、Local Chern marker、Kitaev formula等角度去定义，它们在某种程度上可能有相似或等价之处。以下是我之前查阅过的一些文献，可以作为参考。 1. 和Polarization相关的文献 [1] 1998 - Resta - Quantum-Mechanical Position Operator in Extended Systems https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.80.1800 [2] 2019 - Wheeler et al. - Many-body electric multipole operators in extended systems https://journals.aps.org/prb/abstract/10.1103/PhysRevB.100.245135 [3] 2019 - Kang et al. - Many-body order parameters for multipoles in solids https://journals.aps.org/prb/abstract/10.1103/PhysRevB.100.245134 2. 和Bott index相关的文献 [1] 2010 - Hastings and Loring - Almost commuting matrices, localized Wannier functions, and the quantum Hall effect https://pubs.aip.org/aip/jmp/article-abstract/51/1/015214/231689/ [2] 2010 - Loring and Hastings - Disordered topological insulators via C ast -algebras https://iopscience.iop.org/article/10.1209/0295-5075/92/67004 [3] https://topocondmat.org/w8_general/invariants.html [4] 2018 - Huang and Liu - Quantum Spin Hall Effect and Spin Bott Index in a Quasicrystal Lattice https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.126401 [5] 2018 - Huang and Liu - Theory of spin Bott index for quantum spin Hall states in nonperiodic systems https://journals.aps.org/prb/abstract/10.1103/PhysRevB.98.125130 [6] 2022 - Toniolo - On the Bott index of unitary matrices on a finite torus https://link.springer.com/article/10.1007/s11005-022-01602-6 3. 和Local Chern marker相关的文献 [1] 2011 - Bianco and Resta - Mapping topological order in coordinate space https://journals.aps.org/prb/abstract/10.1103/PhysRevB.84.241106 [2] 2015 - Tran et al. - Topological Hofstadter insulators in a two-dimensional quasicrystal https://journals.aps.org/prb/abstract/10.1103/PhysRevB.91.085125 [3] 2018 - Gebert - Local Chern Number for Noninteracting Fermions in the Harper-Hofstadter Model https://www.uni-frankfurt.de/84038543/Bachelor_Thesis_Gebert_1.pdf [4] 2022 - Dai et al. - Current carrying states in the disordered quantum anomalous Hall effect https://iopscience.iop.org/article/10.1088/1674-1056/ac5d2b 4. 和Kitaev formula相关的文献 [1] 2006 - Kitaev - Anyons in an exactly solved model and beyond https://www.sciencedirect.com/science/article/abs/pii/S0003491605002381

  65. 头像
  66. 头像

    “饭”属于非晶，可能不大好定义拓扑不变量，可以从实空间的角度或者大元胞的角度进行考虑，或者可以查查文献看有没有这方面的研究。另外除了做饭，做个“费米面”也是不错的选择。

  67. 头像

    关老师做出来的饭具有拓扑不变量吗？

  68. 头像
  69. 头像
  70. 头像
  71. 头像
  72. 头像

    您好，想问一下这里自旋陈数的计算看起来和陈数的计算是一样的，因为两个自旋的子空间是解耦的，所以可以分别计算，这样定义的自旋陈数和PHYSICAL REVIEW B 80, 125327, 2009自旋陈数的定义看起来是不同的

  73. 头像

    c相当于数值计算中磁场B的取值，也就是一个量子磁通的1/c倍。如果c为1，表示的是磁场的选取刚好使得磁通为一个量子。

  74. 头像
  75. 头像

    这里的chiral symmetry和手性分子的那种结构手性不是完全对应的，属于概念的延伸吧，最早应该是在粒子物理中描述无质量的狄拉克费米子引入的，从波函数的结构上区分了左右，定义了手性/手征。在凝聚态物理中，有类似的准粒子，具有相同的数学结构。 参考： [1] https://en.wikipedia.org/wiki/Chirality_(physics)#Chiral_symmetry [2] Chirality和Helicity

  76. 头像
  77. 头像
  78. 头像
  79. 头像

    我把tx和ty换成不同的值，验算的结果是对的上的，好像没问题。 如果对不上，把张量积的顺序对调一下就可以了，或者前面的编号重新编写，把y方向的先编号。 也可以不用管，虽然矩阵形式是不一样了，但物理量结果是一样的，影响不大。

  80. 头像

    博主 你的张量积哈密顿量是有问题的，你可以做符号运算，把tx ty带进去，可以发现结果和示意图下那个有tx ty的矩阵不一样，刚好tx ty反了

  81. 头像
  82. 头像
  83. 头像
  84. 头像

    是可以用迭代的方法进行计算，计算效率会高很多。但算法会比较复杂，因为算局域电流时好像不只是需要算格林函数的对角分块矩阵，可能还需要算格林函数的次对角分块矩阵。 格林函数的对角分块矩阵的计算可以参考这两篇：使用Dyson方程迭代方法计算态密度（附Python代码）、使用Dyson方程计算格林函数的对角分块矩阵（第二种方法）。 格林函数的次对角分块矩阵目前我还没去实现，感兴趣也可以试着用戴森方程去推导一下。

  85. 头像
  86. 头像

    理解了，因为中心区gf是(l*w)×（l*w）的。 不过您这边用的是直接求逆计算格林函数。如果使用迭代的话是否矩阵维度就都减小了呢？也就不用HLC这样的扩大维度的矩阵了？

  87. 头像

    是的，对于自能的计算是没影响，大部分的矩阵元是零。这里之所以要扩大维度，是因为是要计算中心区的整体格林函数，从而获取电流信息，而不是只计算某个分块矩阵的格林函数。这时候，电极自能的矩阵维度要和中心区的整体格林函数维度保持一致，才可以运算。

  88. 头像

    关老师，有一个问题。就是您在本篇的part1代码中的，HLC和HCR矩阵，维度是w×(w*l)的，但是您另外一片篇算电导的代码中就是的h00和h01，维度是w×w。 不过因为HCL中有一大部分都是0，好像不影响。 但是您这篇文章中这么写的原因是什么呢？有特别的含义吗？

  89. 头像
  90. 头像
  91. 头像

    老师，您好，当p= (0.328981519117191+0.007898978069732571j)，说明是平庸的吗还是非平庸，计算结果不是近似0.5或者0. 可以判断是平庸非平庸吗？是不是只要不是0 就是非平庸？

  92. 头像

    谢谢关老师的回复，我找到了一些关于跟子晶格sublattices关联的Bipartite lattices相关资料https://phsites.technion.ac.il/eric/wp-content/uploads/sites/6/2020/07/Amit_Goft-MSc_Thesis-compressed.pdf，对于理解子晶格对称性有很大帮助

  93. 头像

    我个人的理解是，手征对称性会更强调两个子系统或两个子晶格，中心反演对称性则更强调几何结构。破坏石墨烯的中心反演对称性大概率会打破手性对称性吧，但我不确定是否是严格的，或者是否可以通过设计一个超胞作为反例，我没详细考虑和证明过，可以参考 2013 - Bernevig and Hughes - Topological Insulators and Topological Superconductors 这本书的第七章。

  94. 头像

    关老师，请问，中心反演对称性和手性对称性有什么区别和联系吗，比如打破石墨烯的中心反演对称性会打破手性对称性吗

  95. 头像
  96. 头像

    我的意思是，用np.linage.eig求出来的本征值是复数，为什么要用np.real截取其中实数部分而非用np.abs得到绝对值呢（按理来说，求本征值应该算出来的都是实数，±根号下互共轭的最近邻项相乘）

  97. 头像
  98. 头像
  99. 头像
  100. 头像

3. 当前页面留言

以下是当前页面“在线留言”的留言内容。如果需要在当前页面留言，请将页面下滑至最底部。

54 thoughts on “在线留言”

  1. 基础医学在读博四党默默举个手，谢谢您的分享，有在互联网某个角落看到一片自己小天地的感觉，祝您一切顺利，会经常来继续学习~

    回复

  2. 记得之前是查文献看过博主你的一篇关于计算STM图像的文章，一直就把你建的这个网站就存为书签了，时常上来看下。看得出博主是个做科研非常严谨认真的大佬，我是做STM实验的，期待以后能有机会和大佬合作~

    回复

  3. 博主您好，我是拓扑材料计算方向的研一学生，我在wilson loop的计算上面遇到了很大的困难，主要是用wainner tools 计算出的wilson loop 上下不对称，有时线很多很乱，想请教一下您，怎么可以解决。

    回复

  4. 博主，如果用程序框图来表示掷点法求定积分跟实际程序有什么不同吗

    回复

  5. 博主您好！我是学光学的，但有时会卡在凝聚态物理的计算方面，比如要计算线性响应理论的Kubo公式，会被一些量子符号绕晕，想问问您有什么好的文章或者书籍可以推荐的，不胜感激！

    回复

  6. 博主您好，最近有在学习使用Python进行量子计算，目前只基本在学习qutip这个包的使用，但是在学习过程中代码出现了很多的问题不知道该如何去解决。看到您在使用python方面很有经验，希望您能在方便的时候给我推荐一些开源网站，学习的文献或者使用心得，万分感谢。

    回复

  7. 您好，不知道您是否知道python中解紧束缚近似的一个包，pythTB里面有很多参数的设置不是很懂，不知道您是否可以解答一下，比如里面的轨道坐标，不知道具体的物理意义是什么

    回复

  8. 博主您好，我是做固体磁性和拓扑物性交叉的理论计算的一年级博士生，之前学习紧束缚模型时候就经常看你主页的分享，感觉受益匪浅，期待能从博主日后的分享中学会更多！感觉题主对非平衡格林函数和紧束缚模型颇有心得，倘若不冒犯，是否可以添加博主的联系方式以便日后请教学习呢？

    回复

  9. 博主你好，看到你那篇讲SSH模型的wilson-loop后，受益匪浅。然后我就想试着用嵌套wilson-loop计算一下四极拓扑绝缘子的极化指数，但卡在一个地方好久了：就是Wannier波函数的形式。我看相关文献（https://journals.aps.org/prb/abstract/10.1103/PhysRevB.96.245115）里面的形式（6.5），但一直搞不明白。不知道博主是否对相关算法有了解，想请教一下,谢谢！！

    回复

    1. 公式看起来是根据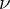\nu矢量的分量，对波函数的线性叠加，然后得到wannier band basis。这个计算方法的实现我之后有空考虑清楚后，可能会更新（也不一定，估计不会很快）。在这个数值计算中应该是会涉及到波函数连续性的问题，还不大好处理，会导致结果不稳定或者错误。

      回复

      1. 是的，我现在计算出来的结果就很奇怪。不知道是在波函数叠加的时候理解错了，还是波函数连续性的问题。好的，那我自己也再看看，谢谢博主！我会经常关注博主的动态的哈哈哈哈，再次感谢！

        回复

  10. 作者你好，我看你画Haldane模型和zigzag的图那篇文章，我想问一下zigzag怎么没有对称性啊，还有作者有画armchair的模型图吗

    回复

    1. 是有对称性呀，可以看看和石墨烯相关的综述文献。armchair模型图目前是没画，只要旋转90度就可以了。

      回复

  11. COOL!!!
    博主你好，看了你的网站，非常丰富，非常有趣。最近我也在尝试将读研期间的学习细致地分享出来，因为感觉科研中有太多重复造轮子的工作。之前是将总结放到github上的，但用github分享总结还是有很多局限。看了你还分享了网站建设的经验，决定也自己尝试以下学习如何自建网站。
    另外，我的研究领域也是量子输运，主要关注高频输运（electron quantum optics），之前是做理论，现在转实验。这次是搜kwant，有幸找到了你的网站。有机会也许可以交流交流，哈哈。

    回复

    1. 嗯，谢谢。很多东西发不了文章，但也是摸索过来的。把一些走的弯路或者一些经验分享出来，或多或少对别人有帮助，同时对自己也有些帮助，笔记整理后思路会更清晰。有需要可以加微信交流，你也可以把你的Github或者之后如果有网站的话也可以分享给我，我可以关注下。

      回复

  12. Dear Jihuan,

    Very interesting works, especially your recent PRB. Look forward to chat more with you in near future.

    Regards,
    Yee Sin
    Singapore University of Technology and Design

    回复

    1. Thanks. I'm also interested in your works and I will pay more attention to your recent publications.

      回复

  13. 博主，你好，看到你跟我是一届的，我感到很惭愧，博主很厉害，很多资料对我有很大的帮助，希望能多跟你请教问题，最后问一下，博主毕业是去哪里高就了？

    回复

    1. 目前还在联系，之后在个人信息的地方会进行更新。你也可以加我微信，有什么可以随时交流~

      回复

      1. 好的，我是做实验的，所以理论部分还比较欠缺，正好看到你的网站分享，对我大有帮助，希望以后能有机会跟你合作！

        回复

  14. 博主您好，对于Kagome Lattice是一个优于石墨烯来研究Haldane模型的体系，博主有没有系统关于Kagome Lattice中的拓扑学习资料推荐？

    回复

    1. 我没怎么接触过这方面的。建议可以翻个qiang用谷歌搜，应该能搜到一些资料或者文献。

      回复

  15. 博主你好，我是初入门python的新手，我想问一下如何建立
    def integral(f,a1,a2)的定积分函数，f是函数，a1a2是上下限

    回复

    2. def integral(f, a1, a2):
    value = 0 # 初始值
    for x in np.arange(a1, a2, 1e-6):  # 1e-6是积分步长
        value = value + f(x)*(1e-6)
    return value  # 返回积分值


      上面是直接积分方法。而蒙特卡洛计算定积分是利用概率得到对应的值。

      回复

  16. 博主您好，我用您提供的LaTeX模板写毕业论文，很好用。
    现在有两个问题请教一下：
    1、如何生成查重用的文件和盲审用的文件。
    2、查重支不支持pdf。
    旁边也没有人可以咨询，如果有可能的话请尽量答复。

    回复

    1. 查重和盲审具体看规定吧。盲审一般会要求把自己的名字和导师的名字省去，然后直接编译生成PDF文件，提交上去就可以了。我最近的学位论文就在盲审阶段（不清楚是否包括查重），通知的是只需要提交一份PDF文件。第二个问题我不大清楚，网上也有很多类似的问题，个人感觉应该是支持PDF的，不放心的话可以问下单位里的相关负责人。

      回复

  19. # 最近邻项
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqr
    请教大神，这一项后面是不是漏了什么

    回复

      1. 你好，楼主，看了你用python写的chern number，很有帮助，但是，想问一下，如果建立一个local gauge的话，如何实现呢？

        回复

        1. 你说的local gauge是指berry curvature吗，已经在代码中实现了呀。有需要可以加我联系方式讨论。

          回复

    1. 薛定谔方程呀，可以网上搜些资料看看。牛顿第二定律F=ma是牛顿力学的基本方程，而薛定谔方程是量子力学的基本方程。

      回复

  23. 使用Latex例子：

    $i\hbar\frac{\partial}{\partial t}\psi(\textbf{r},t)=-\frac{\hbar^{2}}{2m}\nabla^{2}\psi(\textbf{r},t)+V(\textbf{r},t)\psi(\textbf{r},t)$  [latexpage]

    显示为：

    $i\hbar\frac{\partial}{\partial t}\psi(\textbf{r},t)=-\frac{\hbar^{2}}{2m}\nabla^{2}\psi(\textbf{r},t)+V(\textbf{r},t)\psi(\textbf{r},t)$

    回复

发表评论

您的电子邮箱地址不会被公开。 必填项已用 * 标注

Captcha Code