本篇内容主要参考这篇文献:A Short Course on Topological Insulators: Band-structure topology and edge states in one and two dimensions。
1. 模型
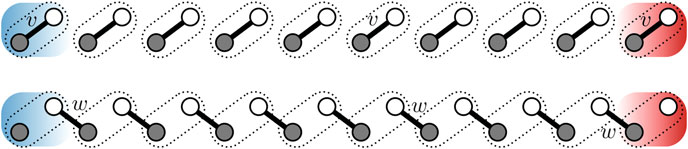
SSH模型示意图如下[1]:

SSH(Su-Schrieffer-Heeger)模型的哈密顿量为:
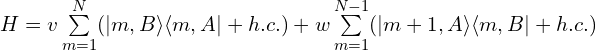
当v=w时,该体系为一维的简单晶格链模型。
2. 能带图
SSH模型哈密顿量经过傅里叶变换后,得到:
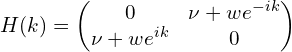
该模型具有手征对称性。可参考这篇:手征对称性 Chiral Symmetry。
画能带图的Python代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5025
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
def hamiltonian(k): # SSH模型
v=0.6
w=1
matrix = np.zeros((2, 2), dtype=complex)
matrix[0,1] = v+w*cmath.exp(-1j*k)
matrix[1,0] = v+w*cmath.exp(1j*k)
return matrix
def main():
k = np.linspace(-pi, pi, 100)
plot_bands_one_dimension(k, hamiltonian)
def plot_bands_one_dimension(k, hamiltonian):
dim = hamiltonian(0).shape[0]
dim_k = k.shape[0]
eigenvalue_k = np.zeros((dim_k, dim))
i0 = 0
for k0 in k:
matrix0 = hamiltonian(k0)
eigenvalue, eigenvector = np.linalg.eig(matrix0)
eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
i0 += 1
for dim0 in range(dim):
plt.plot(k, eigenvalue_k[:, dim0], '-k')
plt.show()
if __name__ == '__main__':
main()
计算结果大概为[1]:

其中,两个极限的情况是w=0或v=0,如下图所示[1]:
3. 卷绕数
这里先给出结论:当v>w时,SSH模型的卷绕数为0;当v<w时,SSH模型的卷绕数为1。
对于具有手征对称性(chiral symmetry)的两带模型,卷绕数(Winding number)的公式为[1]:

计算的Python代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5025
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import time
def hamiltonian(k): # SSH模型
v=0.6
w=1
matrix = np.zeros((2, 2), dtype=complex)
matrix[0,1] = v+w*cmath.exp(-1j*k)
matrix[1,0] = v+w*cmath.exp(1j*k)
return matrix
def main():
start_clock = time.perf_counter()
delta_1 = 1e-9 # 求导的步长(求导的步长可以尽可能短)
delta_2 = 1e-5 # 积分的步长(积分步长和计算时间相关,因此取一个合理值即可)
W = 0 # Winding number初始化
for k in np.arange(-pi, pi, delta_2):
H = hamiltonian(k)
log0 = cmath.log(H[0, 1])
H_delta = hamiltonian(k+delta_1)
log1 = cmath.log(H_delta[0, 1])
W = W + (log1-log0)/delta_1*delta_2 # Winding number
print('Winding number = ', W/2/pi/1j)
end_clock = time.perf_counter()
print('CPU执行时间(min)=', (end_clock-start_clock)/60)
if __name__ == '__main__':
main()
当v=0.6, w=1时,计算结果为(-1):
Winding number = (-1.0000019317691802-1.8464669562815516e-10j)
CPU执行时间(min)= 0.023999098333333337当v=1, w=0.6时,计算结果为(0):
Winding number = (1.1308039592620713e-06-9.492239991615431e-11j)
CPU执行时间(min)= 0.023996206666666665参考资料:
[2] Berry phase effects on electronic properties
[3] 知乎:winding number 的计算公式是怎么来的?
[4] 知乎:陈数(Chern number)与卷绕数(winding number)的区别与联系?
[5] https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%BB%95%E6%95%B0
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
老师您好,如果是四条能带模型,怎么计算winding number呢,我想计算T石墨烯的winding number
我目前没具体算过,但应该还是按定义公式来算,哈密顿量还是需要满足手性这个条件,只是这时候h(k)是一个矩阵。处理方法有可能是对h(k)求本征值,分成两条带分别进行计算,这是我的猜想,不一定对,供参考,你可以查查文献有没有提供四带的结果,计算验证一下。
老师您好,如果哈密顿量不是SSH模型,换成别的模型,请问这个程序还适用吗
嗯,只要满足手征对称性,然后按照着定义公式算应该就没什么问题。
老师你好,我想问问能量本征值是直接求哈密顿矩阵的本征值,而对应的态就是矩阵的对应特征向量吗
是的,就是求定态薛定谔方程的过程,H|i>=E|i>。
您好,请问一下,在每一个计算的模型中,W 和V的值如何确定的?是根据晶格之间的距离么?
跟距离有关,但对应关系不是线性的,可能是指数的,具体看怎么做近似了。如果只是讨论模型,一般是人为直接给的参数。
老师,您好。感谢您的回复。我在comsol中计算模型,但是也想用SSH模型也做一个计算,因此遇到了W 和V的值如何确定,但是不知道如何判断具体W和V值是多少和在comsol中的模型是一样的。因此向您请教一下,我应该怎么做才是对的。
哦哦,这个我也不清楚,我对Comsol不大熟悉。你可以看看Comsol官方文档里有没有相应的说明。如果没有,也可以找一些文献,用一些近似的、和距离有关的coupling表达式。
谢谢老师的解答
老师您好,我试了一下,最后的卷绕数可以通过留数法解析求得,设z=e^(ik),复平面存在两个奇点z=0和z=-w/v,卷绕数等于半径为1的C内的留数和,z=0和z=-w/v对应的留数分别为-1和1,若w>v,则留数和为-1;若w<v,则留数和为-1+1=0。
????
您好,在此模型中卷绕数是否与体系能量有关?卷绕数等于0是否代表体系能量平均分布,等于-1是否代表能量会聚集在某处?通过这个模型的哈密顿量来看,w, v的地位感觉上应该是等同的,为什么v>w时卷绕数会是0,w>v时卷绕数会是-1?而不是 1 和 -1?
(1)卷绕数跟体系能量无关。
(2)卷绕数是一种拓扑不变量,在有限长度时体现的是量子化的边缘态。跟能量平均分布没关系。
(3)如果是无限长的一维链,w和v的地位是相同的,所以在w和v对调后能带完全一样。在算卷绕数的时候,因为涉及到了元胞的选取,这已经包含了有限长度时边缘态的信息。卷绕数取的值跟定义有关,在不具有拓扑时,是定义为0。
可以参考这篇中有关SSH模型的内容或者其他文献:Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators。
极化跟wannier center的位置有关系,从实空间的这个角度去理解也可以。
感谢大佬????
请问数学上陈数应该是个整数才对,可是为什么代码算出来的陈数不是个整数捏(大二学生感到很迷惑)
在计算机中数字都是有位数的,例如单精度浮点数(float)最多有7位十进制有效数字,双精度浮点数(double)表示十进制的15或16位有效数字。在数值计算中,可能会遇到无理数,也会遇到除法运算的无限循环小数,都只是取了有限位数,多次计算后会积累不少误差,所以1e-6以下的值一般不会太准确。还有数值计算中的积分也只是用求和代替,并不是严格的积分。
您好,方便问下哈密顿量是开放条件,那个能带图经过傅里叶变化的哈密顿量是在周期性边界条件下吗?(w项从m=1到N)
能带图必须是在无限长的体系下,才会存在k。因为不是有限长的,所以没有开放条件,也没有周期性边界条件。
能带图k=0的情况,相当于元胞在周期性边界条件下的结果。
您好,这个程序只适用于手对称两能带系统是吗?
从定义来看,是只适用于手对称的系统,但不一定是两能带系统。
如果不满足手对称,可能有其他的拓扑不变量。
好的,谢谢
请问高维度缠绕数的计算是需要先用投影算符降维吗?
没算过,不清楚。可以找下相关文献。
你好,算winding number 的时候选取 的是h(k),如果选取h(k)*的话计算结果是前者的相反数,请问应该选取哪一个?还是只关注其绝对值大小,选取任何一个都可以?
符号其实也跟积分的路径方向有关,一般会用来区分两个路径方向。其他时候只关注绝对值大小,负号影响不大。
你好,我在求解winding number时,加入了一个循环,看u对于winding number的影响,大多数据很正常,为什么中间会出现一个两千多的数字呢?
是v=w的位置吗,这时候带隙为零,能带相交的地方波函数不好区分开。
你好,我想问一下SSH模型那个哈密顿量您知道怎么推导出来的吗?一直很困惑
我谷歌找到了understanding basic concepts of topological insulators through SSH model这篇论文,还找了其中的参考文献[3]oxford solid state physics书,差不多弄懂了这个哈密顿量的来源。不用麻烦您了,打扰了。
嗯嗯,最明显的特征就是交替的跃迁项。