Kagome晶格中的平带（附Mathematica、Python代码）

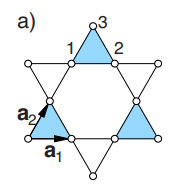
Kagome lattice（笼目结构晶格）示意图[1]：

Kagome晶格在倒空间的哈密顿量[1]：

其中，，以及

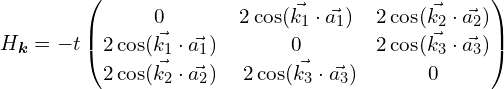
Mathematica符号计算：

Clear["`*"]
k1a1 = kx;
k2a2 = kx/2 + ky*Sqrt[3]/2;
k3a3 = -kx/2 + ky*Sqrt[3]/2;
H = -2*t*({{0, Cos[k1a1], Cos[k2a2]}, {Cos[k1a1], 0, Cos[k3a3]}, {Cos[k2a2], Cos[k3a3], 0}});
MatrixForm[H]
eigenvalue = MatrixForm[Eigenvalues[H]]

计算结果：

Python数值计算（可以用到开源软件包Guan: https://py.guanjihuan.com）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/16730
"""

import numpy as np
from math import *

def hamiltonian(kx, ky):  # kagome lattice
    k1_dot_a1 = kx
    k2_dot_a2 = kx/2+ky*sqrt(3)/2
    k3_dot_a3 = -kx/2+ky*sqrt(3)/2
    h = np.zeros((3, 3), dtype=complex)
    h[0, 1] = 2*cos(k1_dot_a1)
    h[0, 2] = 2*cos(k2_dot_a2)
    h[1, 2] = 2*cos(k3_dot_a3)
    h = h + h.transpose().conj()
    t = 1
    h = -t*h
    return h

def main():
    kx_array = np.linspace(-pi ,pi, 500)
    ky_array = np.linspace(-pi ,pi, 500)
    eigenvalue_array = calculate_eigenvalue_with_two_parameters(kx_array, ky_array, hamiltonian)
    plot_3d_surface(kx_array, ky_array, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', rcount=200, ccount=200)
    
    # import guan
    # eigenvalue_array = guan.calculate_eigenvalue_with_two_parameters(kx_array, ky_array, hamiltonian)
    # guan.plot_3d_surface(kx_array, ky_array, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', rcount=200, ccount=200)

def calculate_eigenvalue_with_two_parameters(x_array, y_array, hamiltonian_function, print_show=0, print_show_more=0):  
    dim_x = np.array(x_array).shape[0]
    dim_y = np.array(y_array).shape[0]
    if np.array(hamiltonian_function(0,0)).shape==():
        eigenvalue_array = np.zeros((dim_y, dim_x, 1))
        i0 = 0
        for y0 in y_array:
            j0 = 0
            for x0 in x_array:
                hamiltonian = hamiltonian_function(x0, y0)
                eigenvalue_array[i0, j0, 0] = np.real(hamiltonian)
                j0 += 1
            i0 += 1
    else:
        dim = np.array(hamiltonian_function(0, 0)).shape[0]
        eigenvalue_array = np.zeros((dim_y, dim_x, dim))
        i0 = 0
        for y0 in y_array:
            j0 = 0
            if print_show==1:
                print(y0)
            for x0 in x_array:
                if print_show_more==1:
                    print(x0)
                hamiltonian = hamiltonian_function(x0, y0)
                eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
                eigenvalue_array[i0, j0, :] = eigenvalue
                j0 += 1
            i0 += 1
    return eigenvalue_array

def plot_3d_surface(x_array, y_array, matrix, xlabel='x', ylabel='y', zlabel='z', title='', fontsize=20, labelsize=15, show=1, save=0, filename='a', file_format='.jpg', dpi=300, z_min=None, z_max=None, rcount=100, ccount=100): 
    import matplotlib.pyplot as plt
    from matplotlib import cm
    from matplotlib.ticker import LinearLocator
    matrix = np.array(matrix)
    fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
    plt.subplots_adjust(bottom=0.1, right=0.65) 
    x_array, y_array = np.meshgrid(x_array, y_array)
    if len(matrix.shape) == 2:
        surf = ax.plot_surface(x_array, y_array, matrix, rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    elif len(matrix.shape) == 3:
        for i0 in range(matrix.shape[2]):
            surf = ax.plot_surface(x_array, y_array, matrix[:,:,i0], rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_zlabel(zlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.zaxis.set_major_locator(LinearLocator(5)) 
    ax.zaxis.set_major_formatter('{x:.2f}')  
    if z_min!=None or z_max!=None:
        if z_min==None:
            z_min=matrix.min()
        if z_max==None:
            z_max=matrix.max()
        ax.set_zlim(z_min, z_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels() + ax.get_zticklabels()
    [label.set_fontname('Times New Roman') for label in labels] 
    cax = plt.axes([0.8, 0.1, 0.05, 0.8]) 
    cbar = fig.colorbar(surf, cax=cax)  
    cbar.ax.tick_params(labelsize=labelsize)
    for l in cbar.ax.yaxis.get_ticklabels():
        l.set_family('Times New Roman')
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

if __name__ == '__main__':
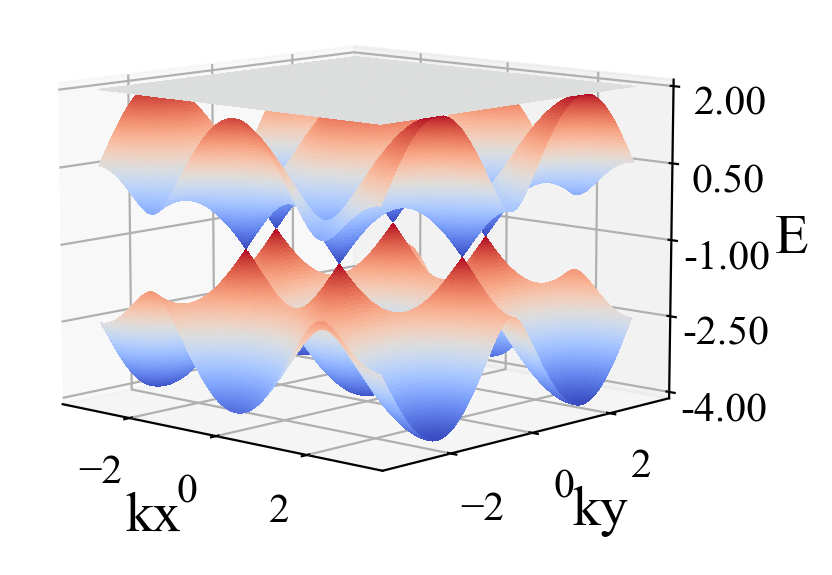
    main()

计算结果：

参考资料：

[1] Topological insulator on the kagome lattice

附：

6,257 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】