陈数Chern number的计算（Kubo公式，附Python代码）

发布时间：2021年7月26日2022年12月24日

最近修改时间：2022年12月24日

另外几篇关于计算陈数的方法：

本篇通过Kubo公式计算陈数。这个方法跟高效法、Wilson loop方法一样，不需要对波函数求导，因此数值计算过程不依赖于波函数相位。

从定义出发，贝里联络（Berry connection）公式为：

$A_n(\bm{R})=i\langle n(\bm{R})|\frac{\partial}{\partial \bm{R}}|n(\bm{R})\rangle$

贝里曲率（Berry curvature）公式：

$\Omega_n(\bm{R})= \nabla_ {\bm{R}} \times A_n(\bm{R})$

展开写为[1]：

$\begin{aligned}\Omega_{\mu\nu}^{n}(\bm{R}) &=\frac{\partial}{\partial R_\mu} A_\nu^n(\bm{R})- \frac{\partial}{\partial R_\nu} A_\mu^n(\bm{R}) \\&= i[\frac{\partial}{\partial R_{\mu}}\langle n(\bm{R})|\frac{\partial}{\partial R_{\nu}}|n(\bm{R})\rangle-(\nu \leftrightarrow \mu)] \end{aligned}$

进一步推导（由“向同学”提供）：

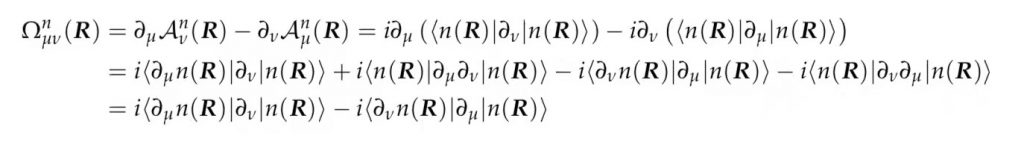
继续推导需要用到以下等式：

$\langle n'|\frac{\partial H}{\partial \bm{R}}|n\rangle = \langle n'| \frac{\partial}{\partial \bm{R}} |n\rangle(E_n-E_{n'})$ for $n'\neq n$

该等式的证明如下[2]。

薛定谔方程： $H|n\rangle =E_n|n\rangle$ 。

两边求导： $\frac{\partial H}{\partial \bm{R}}|n\rangle+H\frac{ \partial |n\rangle}{ \partial \bm{R} }=\frac{\partial E}{\partial \bm{R} }|n\rangle+E_n\frac{ \partial |n\rangle }{ \partial \bm{R} }$ 。

两边左乘 $\langle n'|$ ： $\langle n'| \frac{\partial H}{\partial \bm{R}}|n\rangle+ \langle n'| H\frac{ \partial |n\rangle}{ \partial \bm{R} }= \langle n'| \frac{\partial E_n}{\partial \bm{R} }|n\rangle+ \langle n'| E_n\frac{ \partial |n\rangle }{ \partial \bm{R} }$ 。

整理后： $\langle n'| \frac{\partial H}{\partial \bm{R}}|n\rangle+ E_{n'}\langle n'|\frac{ \partial }{ \partial \bm{R} }|n\rangle=E_n \langle n'|\frac{ \partial }{ \partial \bm{R} }|n\rangle$ 。其中，考虑了 $n'\neq n$ ，因此 $\langle n'| n \rangle = 0$ 。

继续整理，得到： $\langle n'|\frac{\partial H}{\partial \bm{R}}|n\rangle = \langle n'| \frac{\partial}{\partial \bm{R}} |n\rangle(E_n-E_{n'})$ 。证毕！

接下来继续推导贝里曲率公式，考虑贝里曲率中的第一项。

中间插入单位算符 $\sum\limits_{n'} |n'\rangle \langle n'|$ ，得到： $\sum\limits_{n'} \langle \frac{\partial}{\partial R_{\mu}} n| n'\rangle \langle n'| \frac{\partial}{\partial R_{\nu}}|n\rangle$ 。由于贝里曲率后面还有一项 $(\nu \leftrightarrow \mu)$ ，对于 $n' =n$ 的情况两项相减为零，因此这一项可以直接写为： $\sum\limits_{n'\neq n} \langle \frac{\partial}{\partial R_{\mu}} n| n'\rangle \langle n'| \frac{\partial}{\partial R_{\nu}}|n\rangle$ 。

代入上面被证明过的表达式，得到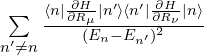： $\sum\limits_{n'\neq n} \frac{ \langle n|\frac{\partial H}{\partial R_{\mu}}|n'\rangle \langle n'|\frac{\partial H}{\partial R_{\nu}}|n\rangle }{(E_n-E_{n'})^2}$

贝里曲率公式：

$\Omega_{\mu\nu}^{n}(\bm{R}) = i \sum\limits_{n'\neq n} \frac{ \langle n|\frac{\partial H}{\partial R_{\mu}}|n'\rangle \langle n'|\frac{\partial H}{\partial R_{\nu}}|n\rangle-(\nu \leftrightarrow \mu) }{(E_n-E_{n'})^2}$

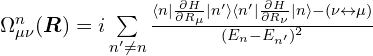
以这篇“陈数Chern number的计算（定义法，附Python/Matlab代码）”中的哈密顿量为例子，计算陈数，Python代码如下（说明：这里只有两条带，所以没有求和。如果存在多条能带，需要对所有其他能带求和）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/16148
"""

import numpy as np
from math import *
import time


def hamiltonian(kx, ky):  # one QAH model with Chern number = 2
    t1 = 1.0
    t2 = 1.0
    t3 = 0.5
    m = -1.0
    matrix = np.zeros((2, 2), dtype=complex)
    matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
    matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
    matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
    matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
    return matrix


def main():
    start_time = time.time()
    n = 200       # integration
    delta = 1e-6  # derivation
    chern_number = 0 
    for kx in np.arange(-pi, pi, 2*pi/n):
        for ky in np.arange(-pi, pi,2*pi/n):
            H = hamiltonian(kx, ky)
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector_0 = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]
            vector_1 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]
            eigenvalue = np.sort(np.real(eigenvalue))

            H_delta_kx = hamiltonian(kx+delta, ky)-hamiltonian(kx, ky) 
            H_delta_ky = hamiltonian(kx, ky+delta)-hamiltonian(kx, ky)

            berry_curvature = 1j*(np.dot(np.dot(np.dot(np.dot(np.dot(vector_0.transpose().conj(), H_delta_kx/delta), vector_1), vector_1.transpose().conj()), H_delta_ky/delta), vector_0)- np.dot(np.dot(np.dot(np.dot(np.dot(vector_0.transpose().conj(), H_delta_ky/delta), vector_1), vector_1.transpose().conj()), H_delta_kx/delta), vector_0))/(eigenvalue[0]-eigenvalue[1])**2

            chern_number = chern_number + berry_curvature*(2*pi/n)**2
    chern_number = chern_number/(2*pi)
    print('Chern number = ', chern_number)
    end_time = time.time()
    print('运行时间(min)=', (end_time-start_time)/60)


if __name__ == '__main__':
    main()

计算结果：Chern number = (-1.9999999999798186+1.9718230813235673e-19j)

补充：Kubo公式也可以推广到简并的情况，计算方法可以看这篇综述文献的公式（73）：First-principle calculations of the Berry curvature of Bloch states for charge and spin transport of electrons。

参考资料：

[1] Quantized Hall Conductance in a Two-Dimensional Periodic Potential

[2] Berry phase effects on electronic properties

[3] https://phyx.readthedocs.io/en/latest/TI/Lecture%20notes/2.html

[4] https://mp.weixin.qq.com/s/VJxeLOIyBoJQ1-x-P4Pwtg

8,151 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

27 thoughts on “陈数Chern number的计算（Kubo公式，附Python代码）”

匿名说道：

2023年8月18日 03:33

您好!请问我在其他晶格中，使用该方法时，假如是蜂窝晶格，其布里渊区的选取可以平移成方形来进行计算吗，感谢您的回复。

回复
1. guanjihuan说道：
  
  2023年8月18日 23:19
  
  应该是可以的，相邻的布里渊区具有等价性。
  
  回复
匿名说道：

2023年6月10日 06:53

您好，我使用当前的代码，对角化函数改为eigh（对角化厄米矩阵）而非eig，最后陈数就不对，是什么原因呢？

回复
1. guanjihuan说道：
  
  2023年6月10日 22:10
  
  结果一样的呀
  
  回复
  1. 匿名说道：
    
    2023年6月11日 03:04
    
    找到问题了，因为arm版本的mac下numpy的数值库有bug.....多谢博主啦！
    
    回复
匿名说道：

2022年12月5日 22:23

请问kubo公式在计算简并能带的陈数是要怎么处理？En-En’=0，最后会有NAN的出现。

回复
1. guanjihuan说道：
  
  2022年12月6日 08:19
  
  可以看这篇综述文献的公式（73）：First-principle calculations of the Berry curvature of Bloch states for charge and spin transport of electrons。。
  
  回复
2. 匿名说道：
  
  2024年10月26日 07:11
  
  考虑非阿贝尔系统的时候，简并子空间里的贝利曲率是一个矩阵而不是标量，每一个矩阵元只对简并子空间之外的能带求和，考虑热平均，简单的说就是你计算第n条带的贝利曲率时，需要对其他所有带求和，但是求和的时候直接忽略和第n条带简并的那些带即可。这个用非阿贝尔的方法很容易证明
  
  回复
匿名说道：

2022年11月28日 03:24

用matlab计算，计算精度完全不一样。
用上面网友给处的方法，算出来的结果是2.0066-7.6367e-20i
自己用matlab写wilson loop方法也是。
精度只能到小数点后2~3位。
想算得足够小， n = 200 # integration 项要非常大。
不知道是什么原因导致的

回复
1. 匿名说道：
  
  2022年11月28日 13:41
  
  哦我找到问题了，是重复计算了边界
  matlab中生成数组 kx=-pi:L:pi;
  结果是 [-pi, -pi+L,-pi+2L,....,pi-L,pi]
  这里出现了-pi和pi, 而这两个点是等价的。
  
  这个点重复统计了两次，
  以上面网友给出的matlab程序为例：
  for循环应该去掉最后一位，改成
  for ii=1:length(kx0)-1
  for jj=1:length(ky0)-1
  .....
  end
  end
  
  回复
  1. guanjihuan说道：
    
    2022年11月29日 01:12
    
    嗯，Matlab的取值范围是左闭右闭的。
    
    回复

写了个matlab版的，结果对的上：

%kubo公式，特点是不用加波函数规范
function []=main_kubo_chen()
tic
n=200;%布里渊区积分离散参数
delta=1e-6;%求导步长,应该是要比积分步长小
c_num=0;%陈数初始化
band_index=1;%算哪条陈数的能带，本征值从低到高
N=2;%哈密顿量矩阵的阶数，也是波函数个数，根据实际情况写
kx0=-pi:2*pi/n:pi;
ky0=kx0;%在第一布里渊区积分

for ii=1:length(kx0)
    for jj=1:length(ky0)
        kx=kx0(ii);
        ky=ky0(jj);
        H=hami(kx,ky);
        [eigen_vecor,eigen_value]=eig(H);
        
         [e_value,index]=sort(real(diag(eigen_value)));
         wave_fun_matrix=eigen_vecor(:,index);%按照本征值从小到大排列波函数
         
         D_H_kx = (hami(kx+delta, ky)-hami(kx, ky))/delta;%矩阵，求导
         D_H_ky = (hami(kx, ky+delta)-hami(kx, ky))/delta;%矩阵
         
         berry_cur=0;%贝利曲率初始化
         
         wave_fun0=wave_fun_matrix(:,band_index);%|n>
         value0=e_value(band_index);%En
         for uu=1:N
             if uu==band_index
                 continue
             end
             
             temp_wave_fun=wave_fun_matrix(:,uu);%|n'>
             temp_value=e_value(uu);%En'
             
             a1=wave_fun0'*D_H_kx*temp_wave_fun*temp_wave_fun'*D_H_ky*wave_fun0;
             a2=wave_fun0'*D_H_ky*temp_wave_fun*temp_wave_fun'*D_H_kx*wave_fun0;
             
             berry_cur=berry_cur+1j*(a1-a2)/(value0-temp_value)^(2);
         end
         %贝利曲率计算完毕,berry_cur
         c_num=c_num+berry_cur*((2*pi/n)^2);
    end
end

c_num=c_num/(2*pi);

disp(['第',num2str(band_index),'条能带陈数为:',num2str(c_num)])
toc
end




function  [out]=hami(kx,ky)
%一个测试哈密顿量
t1 = 1.0;
t2 = 1.0;
t3 = 0.5;
m = -1.0;
matrix =zeros(2);
matrix(1, 2) = 2*t1*cos(kx)-1j*2*t1*cos(ky);
matrix(2,1) = 2*t1*cos(kx)+1j*2*t1*cos(ky);
matrix(1,1) = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky);
matrix(2,2) = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky));
out=matrix;
end

guanjihuan说道：

2021年8月12日 23:03

嗯，用的公式一样的吧

回复
1. 匿名说道：
  
  2021年8月13日 20:56
  
  就是根据您py版改写的
  
  回复
  1. 匿名说道：
    
    2021年12月20日 19:07
    
    这个久保公式法在有能带兼并的时候咋办，En-En’=0，发散了，数值是缺失值NAN
    
    回复
    1. guanjihuan说道：
      
      2021年12月21日 10:18
      
      我可以先试着加微扰打开带隙吧。或者把价带波函数当成整体来算？这个我还没验证过。
      
      回复
      1. 匿名说道：
        
        2022年2月14日 20:22
        
        https://journals.jps.jp/doi/10.1143/JPSJ.73.2604
        
        回复
        
        guanjihuan说道：
        
        2022年2月15日 11:21
        
        感谢提供的文献！
        
        回复
匿名说道：

2022年4月17日 17:18

你好，这个matlab代码可以画3维的贝里曲率图吗？z轴是贝里曲率，x、y轴分别是kx、ky那种，谢谢~

回复
1. guanjihuan说道：
  
  2022年4月17日 19:53
  
  可以的，不求和就是贝里曲率的分布，求和就是陈数。
  
  回复
  1. 匿名说道：
    
    2022年4月18日 10:01
    
    可否具体出一个画3维贝里曲率图形的matlab代码，我修改了一番这个评论区的求陈数的代码，没有画出来贝里曲率图，感谢指导~
    
    回复
    1. guanjihuan说道：
      
      2022年4月21日 13:02
      
      其实也不需要改多少，最后没有求和，就是贝里曲率分布。目前没有matlab代码，可以参考这篇：贝里曲率的计算（附Python代码）。
      
      回复
      1. 匿名说道：
        
        2022年4月21日 15:20
        
        好嘞，谢谢~
        
        回复

匿名说道：

2021年8月11日 14:54

算的是最低能带对应的陈数吗

回复
1. guanjihuan说道：
  
  2021年8月12日 22:07
  
  嗯，是价带，这里是两条带的最低带。
  
  回复
匿名说道：

2021年8月10日 19:35

好像计算陈数还有个kubo公式的方法，威尔逊环等方法，我见过的就有四五种。

回复
1. guanjihuan说道：
  
  2021年8月10日 20:33
  
  嗯，是还有其他几种方法，都是等价的。
  
  回复

Published by guanjihuan

27 thoughts on “陈数Chern number的计算（Kubo公式，附Python代码）”

发表评论 取消回复

发表评论取消回复