拓扑不变量, 学术

陈数Chern number的计算（高效法，附Python/Matlab代码）

发布时间：

最近修改时间：2024年12月19日

定义法计算陈数参考这篇：陈数Chern number的计算（定义法，附Python/Matlab代码）。

此外还有：

本篇采用的是参考文献[1]中的方法，这里截图一部分出来：

以参考文献[2]中量子反常霍尔模型为例子。Python代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4179
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time


def hamiltonian(kx, ky):  # 量子反常霍尔QAH模型（该参数对应的陈数为2）
    t1 = 1.0
    t2 = 1.0
    t3 = 0.5
    m = -1.0
    matrix = np.zeros((2, 2))*(1+0j)
    matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
    matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
    matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
    matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
    return matrix


def main():
    start_time = time.time()
    n = 100 
    delta = 2*pi/n
    chern_number = 0  # 陈数初始化
    for kx in np.arange(-pi, pi, 2*pi/n):
        for ky in np.arange(-pi, pi, 2*pi/n):
            H = hamiltonian(kx, ky)
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
           
            H_delta_kx = hamiltonian(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
            
            H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
            
            Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
            Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
            Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
            Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

            F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))

            # 陈数(chern number)
            chern_number = chern_number + F
    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_time = time.time()
    print('运行时间(min)=', (end_time-start_time)/60)


if __name__ == '__main__':
    main()

计算结果为：

Chern number = (1.9999999999999998-1.7272599290109276e-16j)

Matlab代码：

% This code is supported by the website: https://www.guanjihuan.com
% The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4179

% 陈数高效法
clear;clc;
n=100 % 积分密度
delta=2*pi/n;
C=0; 
for kx=-pi:(2*pi/n):pi-(2*pi/n)
    for ky=-pi:(2*pi/n):pi-(2*pi/n)
        VV=get_vector(HH(kx,ky));
        Vkx=get_vector(HH(kx+delta,ky)); % 略偏离kx的波函数
        Vky=get_vector(HH(kx,ky+delta)); % 略偏离ky的波函数
        Vkxky=get_vector(HH(kx+delta,ky+delta)); % 略偏离kx，ky的波函数
        
        Ux = VV'*Vkx/abs(VV'*Vkx);
        Uy = VV'*Vky/abs(VV'*Vky);
        Ux_y = Vky'*Vkxky/abs(Vky'*Vkxky);
        Uy_x = Vkx'*Vkxky/abs(Vkx'*Vkxky);
        
        % berry curvature
        F=log(Ux*Uy_x*(1/Ux_y)*(1/Uy));
        % chern number
        C=C+F;  
    end
end
C=C/(2*pi*1i)

function vector_new = get_vector(H)
[vector,eigenvalue] = eig(H);
[eigenvalue, index]=sort(diag(eigenvalue), 'descend');
vector_new = vector(:, index(2));
end

function H=HH(kx,ky)
H(1,2)=2*cos(kx)-1i*2*cos(ky);
H(2,1)=2*cos(kx)+1i*2*cos(ky);
H(1,1)=-1+2*0.5*sin(kx)+2*0.5*sin(ky)+2*cos(kx+ky);
H(2,2)=-(-1+2*0.5*sin(kx)+2*0.5*sin(ky)+2*cos(kx+ky));
end

补充说明1：高效法中的偏移量和积分步长要保持一致才行。

补充说明2：公式定义中的\tilde{F}本身已经包含了步长，所以最后只要直接求和就可以了，在文献[1]中的Eq.12到Eq.13之间有提到，见下面的截图。所以，如果要得到贝里曲率，\tilde{F}还需要除以两个方向的步长。可以大概这么去理解：通常定义的贝里联络A需要对k求导，但在文献[1]中定义的\tilde{A}中只有偏移量，没有除以步长。如果对\tilde{A}做一个泰勒展开，和A刚好就差一个步长。

参考资料：

[1] Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances

[2] Route towards Localization for Quantum Anomalous Hall Systems with Chern Number 2

17,967 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

头像

Published by guanjihuan

93 thoughts on “陈数Chern number的计算（高效法，附Python/Matlab代码）”

  1. 老师，您好，关于这个高阶拓扑绝缘体体极化系数的计算，有相关matlab的程序吗？

    回复

    1. 应该不能直接用吧，非厄米系统的拓扑不变量的定义应该是不一样的，可能需要做一些修改。具体你需要根据定义的公式进行计算，这里经典的陈数定义只能作为参考。

      回复

  3. 您好，高效法算陈数算的好慢，是我代码的问题还是这个方法就这么慢啊，我看用kubo fomulator算陈数几秒钟就算完了

    回复

    1. 应该是算法本身的问题，公式是等价的，只是计算效率不同，计算结果是一样的。

      回复

      1. 我算了转角体系几百×几百的哈密顿量，用高效法算陈数算了二十分钟正常吗？感觉好慢，但最后结果是对的

        回复

        1. 嗯，正常的吧，你这个体系还是比较大的，在误差范围内，也可以适当地减少计算精度。另外，Python本身计算速度不是特别快，如果追求计算效率，可以考虑使用Numba加速Python的时间测试，或者使用Fortran语言来写。

          回复

  4. 您好，我參考了您的文章 寫了一個程式計算QWZ model ,
    我的做法是直接用for loop 變動及儲存 每個kx , ky 的值
    最後做循環內積，但結果一直不太正確 ， 不知道能不能請教您具體的問題可能出在哪裡。

    
u = 2 ;
H = zeros( 2 , 2 );

sigmax = [ 0 , 1 ; 1 , 0 ];
sigmay = [ 0 , -i ; i , 0 ];
sigmaz = [ 1 , 0 ; 0 , -1 ];

for nkx = 1 : Nk
    for nky = 1 : Nk

        H = sin(kx(nkx)) * sigmax + sin(ky(nky)) * sigmay +( u + cos(kx(nkx)) + cos(ky(nky)) ) * sigmaz; 
        
        [ V , D ] = eig(H);
        
        [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) )  ) ;
          ES( nkx , nky , : ) = V( : , ind(1) )   ;
             
    end
end


Nk2 = zeros( Nk-1 , Nk-1);


for nx = 1:Nk-1
    for ny = 1:Nk-1
         
        M1 = sum ( conj( ES( nx , ny , :) ) .* ES1( nx+1 , ny , : ) ,3  ) ;
        M2 = sum ( conj( ES( nx+1 , ny , :) ) .* ES1( nx+1 , ny+1 , : ) ,3 );
        M3 = sum ( conj( ES( nx+1 , ny+1 , :) ) .* ES1( nx , ny+1 , : ) ,3 );
        M4 = sum ( conj( ES( nx , ny+1 , :) ) .* ES1( nx , ny , : ) , 3 );

        M = M1 * M2 * M3 * M4 ;
        CV = -imag( log (M) ) ;
        Nk2( nx , ny ) = CV ;
    end
end


X = Nk2(:) ; 
Y = sum(X);  
Z=sum(X)/2/pi; % chern number
set(gca,'xticklabel',[]);
set(gca,'yticklabel',[]);

    回复

    1. 这个代码好像缺少一些变量，没法直接运行。我一时也没法马上看出来，你可以检查下：（1）检查这个哈密顿量的布里渊区范围，这决定了积分的范围。（2）检查这个能带是否有交叉或简并的情况，如果有简并，可以参考这篇：陈数Chern number的计算（多条能带的高效法，附Python代码）。（3）还有一个简单的检查方法是：你把哈密顿量换成博文中的例子，看结果是否正确，用来验证其他代码是不是对的，如果不对，可以把Nk取很小，然后一步步看具体的数值差异在哪里。

      回复

      1. 謝謝您的回覆，上述的代碼我少附了定義布里渊区范围的參數。
        重新附上一份完整的內容，關於上述您提到我可以檢查的方式我目前都有檢查過。
        我有試著使用您的程式碼來測試我的哈密頓量所計算出的陳數，似乎是沒有問題的。

        我認為到給出哈密頓量的部分都沒有問題，我也有解出能譜結構是沒問題的。問題似乎是出現在後續給解出本徵相量Ｖ和做循環內積時，不知道是否我有哪個地方的邏輯不太正確。

        
clc
clear all
close all


Nk = 1000;


kx = linspace( -pi , pi , Nk );
ky = kx;

u = 2 ;
H = zeros( 2 , 2 );

sigmax = [ 0 , 1 ; 1 , 0 ];
sigmay = [ 0 , -i ; i , 0 ];
sigmaz = [ 1 , 0 ; 0 , -1 ];

for nkx = 1 : Nk
    for nky = 1 : Nk

        H = sin(kx(nkx)) * sigmax + sin(ky(nky)) * sigmay +( u + cos(kx(nkx)) + cos(ky(nky)) ) * sigmaz; 
        
        [ V , D ] = eig(H);
        
        [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) )  ) ;
         ES1( nkx , nky , : ) = V( : , ind(1) )   ;
             
    end
end


Nk2 = zeros( Nk-1 , Nk-1);


for nx = 1:Nk-1
    for ny = 1:Nk-1
         
        M1 = sum ( conj( ES1( nx , ny , :) ) .* ES1( nx+1 , ny , : ) ,3  ) ;
        M2 = sum ( conj( ES1( nx+1 , ny , :) ) .* ES1( nx+1 , ny+1 , : ) ,3 );
        M3 = sum ( conj( ES1( nx+1 , ny+1 , :) ) .* ES1( nx , ny+1 , : ) ,3 );
        M4 = sum ( conj( ES1( nx , ny+1 , :) ) .* ES1( nx , ny , : ) , 3 );

        M = M1 * M2 * M3 * M4 ;
        CV = -imag( log (M) ) ;
        Nk2( nx , ny ) = CV ;
    end
end

%[ kkx , kky ] = meshgrid( kx(1:Nk-1) , ky(1:Nk-1) ) ;

surfc ( Nk2 ) ; % shading interp

X = Nk2(:) ; % n x n brillouin zone  -> 1D ex: [1,2,;3,4]->[1,2,3,4]
Y = sum(X);  
Z=sum(X)/2/pi; % chern number
set(gca,'xticklabel',[]);
set(gca,'yticklabel',[]);

        回复

        1. 我问了GPT，这样修改好像就可以了（具体哪里出错，可以自己检查下，我也没仔细看）：

          这个
          [ EV( nky , nkx , : ) , ind ] = sort( ( sqrt( diag(D) ) ) ) ;
          修改成
          [~, ind] = sort(diag(D)); % Sort eigenvalues
          V = V(:, ind); % Sort eigenvectors accordingly

          另外你这个模型运行结果是 -0.5，我不知道是什么原因。如果改成博文中的模型，结果是 -2，好像没什么问题。

          H(1,2)=2*cos(kx(nkx))-1i*2*cos(ky(nky));
          H(2,1)=2*cos(kx(nkx))+1i*2*cos(ky(nky));
          H(1,1)=-1+2*0.5*sin(kx(nkx))+2*0.5*sin(ky(nky))+2*cos(kx(nkx)+ky(nky));
          H(2,2)=-(-1+2*0.5*sin(kx(nkx))+2*0.5*sin(ky(nky))+2*cos(kx(nkx)+ky(nky)));

          回复

        2. 我试着画了下你这个模型的能带，是一个半金属，没有带隙，在狄拉克点/外尔点的位置没法确定导带和价带，这可能是算出来是 -0.5 的原因，这个结果应该不是物理的。

          回复

          1. 非常感謝您的回覆，這個model是參考了"a short course on topological insulators"的內容。我有重新讀了一下關於這個model的內容，文章中透過解析解的方式有給出了陳數與u的關係，我推測會跑出-0.5是因為當我選取的u=2時剛好落在 0<u2 此時可能只包到了半個參考點。 我有測試過符合區間內的u，結果都符合解析出來的預期。

            回复

  5. 关教授您好，我最近复现了这篇https://iopscience.iop.org/article/10.1088/0953-8984/27/4/045601/pdf关于量子反常霍尔QAH模型，这篇文章中的哈密顿量和您参考文献中的哈密顿量明明是一样的，为什么相图中陈数的数值会相差一个负号呀。我在计算bott index的过程中发现我的相图在一些区域还是有正负号的差别，难道说这个正负号不影响计算结果？

    这个问题困扰我蛮久，期待您的回复，谢谢您。

    回复

    1. 这个可能和模型的参数或相位有关。或者是跟跃迁强度t的正负号有关，这直接决定了能带是否上下颠倒。

      对于给定的哈密顿量，如果计算出来的陈数结果都是刚好正负号相反，那么结果应该是没问题。如果是有的正，有的负，这个还不好说，可以检查下价带的总陈数的符号是否保持稳定，如果总陈数的符号不稳定，那么结果就是有问题，这是因为对于确定的体系，手性边缘态的方向是固定的。

      回复

    1. 有了解一些，但目前没详细做过计算，好像可以从Polarization、Bott index、Local Chern marker、Kitaev formula等角度去定义，它们在某种程度上可能有相似或等价之处。以下是我之前查阅过的一些文献，可以作为参考。

      1. 和Polarization相关的文献
      [1] 1998 - Resta - Quantum-Mechanical Position Operator in Extended Systems https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.80.1800
      [2] 2019 - Wheeler et al. - Many-body electric multipole operators in extended systems https://journals.aps.org/prb/abstract/10.1103/PhysRevB.100.245135
      [3] 2019 - Kang et al. - Many-body order parameters for multipoles in solids https://journals.aps.org/prb/abstract/10.1103/PhysRevB.100.245134

      2. 和Bott index相关的文献
      [1] 2010 - Hastings and Loring - Almost commuting matrices, localized Wannier functions, and the quantum Hall effect https://pubs.aip.org/aip/jmp/article-abstract/51/1/015214/231689/
      [2] 2010 - Loring and Hastings - Disordered topological insulators via C ast -algebras https://iopscience.iop.org/article/10.1209/0295-5075/92/67004
      [3] https://topocondmat.org/w8_general/invariants.html
      [4] 2018 - Huang and Liu - Quantum Spin Hall Effect and Spin Bott Index in a Quasicrystal Lattice https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.126401
      [5] 2018 - Huang and Liu - Theory of spin Bott index for quantum spin Hall states in nonperiodic systems https://journals.aps.org/prb/abstract/10.1103/PhysRevB.98.125130
      [6] 2022 - Toniolo - On the Bott index of unitary matrices on a finite torus https://link.springer.com/article/10.1007/s11005-022-01602-6

      3. 和Local Chern marker相关的文献
      [1] 2011 - Bianco and Resta - Mapping topological order in coordinate space https://journals.aps.org/prb/abstract/10.1103/PhysRevB.84.241106
      [2] 2015 - Tran et al. - Topological Hofstadter insulators in a two-dimensional quasicrystal https://journals.aps.org/prb/abstract/10.1103/PhysRevB.91.085125
      [3] 2018 - Gebert - Local Chern Number for Noninteracting Fermions in the Harper-Hofstadter Model https://www.uni-frankfurt.de/84038543/Bachelor_Thesis_Gebert_1.pdf
      [4] 2022 - Dai et al. - Current carrying states in the disordered quantum anomalous Hall effect https://iopscience.iop.org/article/10.1088/1674-1056/ac5d2b

      4. 和Kitaev formula相关的文献
      [1] 2006 - Kitaev - Anyons in an exactly solved model and beyond https://www.sciencedirect.com/science/article/abs/pii/S0003491605002381

      回复

  7. 您好，首次接触到陈数的概念，有些问题想要问一下。了解到如果要计算一维的陈数，那么这个系统需要在一维周期空间晶格和另一个周期参数t形成的外势中。那么如果该系统是两分量，且在只有一维周期晶格中，那么是否能求陈数呢？

    回复

    1. 嗯，陈数一般是定义在二维上。如果是一维加上其他周期参数，可能也是可以定义的，具体我不大了解，你可以查查文献看有没有相关的定义。重点应该在于这个周期性参数的周期是否可以作为赝布里渊区的一个分量。

      回复

  8. 关教授您好，很漂亮的代码，谢谢您的分享。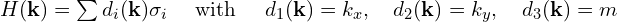
    我用Dirac模型 H(\mathbf{k})=\sum d_{i}(\mathbf{k}) \sigma_{i} \quad \text { with } \quad d_{1}(\mathbf{k})=k_{x}, \quad d_{2}(\mathbf{k})=k_{y}, \quad d_{3}(\mathbf{k})=m, 对应的拓扑不变量为 sign(m)/2, 但是我只是替换了您代码的哈密顿量部分, 用高效陈数法和定义法得到的结果并不理想，我不知道是什么原因，期望可以指教下。
    下面是具体代码matlab% 陈数高效法

    clear;clc;tic;
n=1000; % 积分密度
delta=2*pi/n;

C=0; 
for kx=-pi:(2*pi/n):pi
    for ky=-pi:(2*pi/n):pi
        VV=get_vector(HH(kx,ky));
        Vkx=get_vector(HH(kx+delta,ky)); % 略偏离kx的波函数
        Vky=get_vector(HH(kx,ky+delta)); % 略偏离ky的波函数
        Vkxky=get_vector(HH(kx+delta,ky+delta)); % 略偏离kx，ky的波函数
        
        Ux = VV'*Vkx/abs(VV'*Vkx);
        Uy = VV'*Vky/abs(VV'*Vky);
        Ux_y = Vky'*Vkxky/abs(Vky'*Vkxky);
        Uy_x = Vkx'*Vkxky/abs(Vkx'*Vkxky);
        
        % berry curvature
        F=log(Ux*Uy_x*(1/Ux_y)*(1/Uy));
        % chern number
        C=C+F;  
    end
end

C=C/(2*pi*1i)
toc

function vector_new = get_vector(H)
[vector,eigenvalue] = eig(H);
[~, index]=sort(diag(eigenvalue), 'descend');
vector_new = vector(:, index(2));
end

function H=HH(kx,ky)
sx=[0,1;1,0];sy=[0,-1i;1i,0];sz=[1,0; 0,-1];
  m=2;
H = kx*sx+ky*sy+m*sz;
end


    期待您的回复。

    回复

    1. 你的这个哈密顿量是局域的连续模型，没有布里渊区，所以没法积分，没法算陈数。可以通过sin(x)≈x等近似操作变成紧束缚的形式，但这种操作也不一定对，在局域点上可能是合理的。

      回复

  9. 关老师，我想问一下，kubo公式法，高效法，Wilson loop法，这些方法有本质的区别吗

    回复

    1. 没什么区别，方法是等价的，和陈数的定义一致。只是通过公式的替代和推导得到了其他的一些形式，方便数值计算。

      回复

    1. 对于拓扑绝缘体，霍尔电导中的整数值等于陈数，是等价的。如果是其他体系，例如金属，就不一定是等价的，可能需要从量子输运的角度来计算。

      回复

      1. 谢谢您百忙之中的回复， 再麻烦您一下，就是我最近想计算磁子系统中非厄米哈密顿量的霍尔系数，却迟迟不得以实现，请问您对这方面有所了解吗？

        回复

        1. 我目前没做非厄米的系统，对这个了解不多。你可以看看这方面的文献以及相应的公式。

          回复

            1. 您好 抱歉再次打扰您，请问您有了解波色子 （Bogoliubov–de Gennes）Bdg系统中的陈数计算吗？

              回复

    2. 关老师您好！请问一下，我用两层4带模型计算陈数，结果一直不对，麻烦您能告诉我可能的原因吗?以下是我的代码：

      clear
      close

      n=400;
      delta=2*pi/n;
      C=0;

      for kx=-pi:(2*pi/n):pi-delta
      for ky=-pi:(2*pi/n):pi-delta
      VV=get_vector(HH(kx,ky));
      Vkx=get_vector(HH(kx+delta,ky)); % 略偏离kx的波函数
      Vky=get_vector(HH(kx,ky+delta)); % 略偏离ky的波函数
      Vkxky=get_vector(HH(kx+delta,ky+delta)); % 略偏离kx，ky的波函数

      Ux = VV'*Vkx/abs(VV'*Vkx);
      Uy = VV'*Vky/abs(VV'*Vky);
      Ux_y = Vky'*Vkxky/abs(Vky'*Vkxky);
      Uy_x = Vkx'*Vkxky/abs(Vkx'*Vkxky);

      % berry curvature
      F=log(Ux*Uy_x*(1/Ux_y)*(1/Uy));
      % chern number
      C=C+F;
      end
      end
      C=imag(C)/(2*pi);

      function vector_new = get_vector(H)
      [vector,eigenvalue] = eig(H);
      [~, index]=sort(diag(real(eigenvalue)), 'descend'); % 按实部排序
      vector_new = vector(:, index(4));
      end

      function H=HH(kx,ky)
      r_im=0.5;
      t=1;
      t0=0.5;
      H(1, 1)=0;
      H(1, 2)=t+t*exp(-1i*ky)+t0*(exp(1i*kx)+exp(-1i*kx));
      H(1, 3)=2i*r_im*sin(kx);
      H(1, 4)=0;

      H(2, 1)=t+t*exp(1i*ky)+t0*(exp(1i*kx)+exp(-1i*kx));
      H(2, 2)=0;
      H(2, 3)=0;
      H(2, 4)=-2i*r_im*sin(kx);

      H(3, 1)=-2i*r_im*sin(kx);
      H(3, 2)=0;
      H(3, 3)=0;
      H(3, 4)=t+t*exp(-1i*ky)+t0*(exp(1i*kx)+exp(-1i*kx));

      H(4, 1)=0;
      H(4, 2)=2i*r_im*sin(kx);
      H(4, 3)=t+t*exp(1i*ky)+t0*(exp(1i*kx)+exp(-1i*kx));
      H(4, 4)=0;
      end

      回复

  12. 老师您好我目前有关于C4算拓扑体极化的代码（其中数据由comsol导出），我想在这基础上算有关C6的拓扑体极化，需要在C4基础上改哪些内容

    回复

    1. 布里渊区不一样，而且可能需要考虑具体某个极化的方向吧，不同极化方向选择的k路径不一样。可以查这方面的文献看看，我目前没做过这个

      回复

  13. 您好，请问这个计算方法对于布里渊区不为长方形的情形有效吗？比如对菱形区域的布里渊区？是否要乘上一个系数？

    回复

      1. 老师您好!为什么您的Matlab程序最后求陈数积分的时候的时候不需要乘以步长

        回复

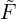        1. 公式定义中的\tilde{F}本身已经包含了步长，所以最后只要直接求和就可以了，在文献[1]中的Eq.12到Eq.13之间有提到。所以如果要得到贝里曲率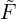，\tilde{F}还需要除以两个方向的步长。可以大概这么去理解：通常定义的贝里联络A需要对k求导，但在定义的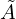\tilde{A}中只有偏移量，没有除以步长。如果对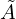\tilde{A}做一个泰勒展开，和A刚好就差一个步长。

          回复

  14. 您好，我用了这些代码之后发现有些带算出来的结果和我取得n有关，请问是什么原因，比如我取n=40，就会有些带的陈数是80

    回复

  15. 关博士您好，请问能带的陈数一定是整数吗？我计算过程中遇到用价带陈数相加作为体系的陈数的情况，这时各个价带的陈数可以不是整数吗？

    回复

    1. 如果不存在能带简并或交叉以及电子半填充的情况，单条能带携带的陈数应该都要为整数。

      回复

  16. 请问大佬，这四种方法有可以用来算那种能带存在简并的体系吗（6*6的矩阵只有三个带），我自己试了一下，发现算出来的陈数对不上，请问有啥方法解决吗，跪求！！！

    回复

        1. 非常感谢。我也在您的另一篇博客（haldan模型）中看到评论中有人推广到简并情况，我最终的目的是计算简并二阶陈数，c2=1/（4pi∧2）sum（F_xyF_zw+F_xzF_yw+F_xwF_zy）请问可以先用一阶的方法算出F_xy, F_zw, F_xz等六项再带入计算二阶陈数吗？

          回复

          1. 我不了解你这个二阶陈数的概念，要确保F_xy等项是被良好定义的，是不是和这里定义的一样。另外如果是简并的，波函数可能会出现问题，因为波函数的任意线性组合都是简并能带的波函数。我不确定是不是可以直接用，你也可以测试下看算得对不对。

            回复

            1. 我有做过测试计算4维狄拉克模型（二重简并）的second chern number。但是很奇怪，计算结果随着delta_k 的取值有很大变化（四个纬度delta_k一致，由于计算量的关系 ，我最小试到delta_k=2pi/50），偶尔才能与理论结果一致。如果您愿意并且有时间的话，我可以加您微信一起讨论一下可能的原因吗？非常感谢

              回复

              2. 问下，双重狄拉克锥情况陈数算出来了，如果算出来了，我想出价购买代码可否？感恩~

                回复

  18. 关老师你好，请问一下这个方法适用于平移对称被破坏的实空间哈密顿量吗？

    回复

    1. 这个是在倒空间计算的，是二维的体系。如果没有空间平移对称性，可以考虑周期性边界条件，认为是无限大的，也可以考虑实空间计算陈数的方法，我目前还没算过，你可以查查文献。

      回复

  19. vector_new = vector(:, index(2));
    请问这里的index（2）是要随着哈密顿的维度而改变吗，假如我要算的是8X8的哈密顿量那就是index（8）吧

    回复

    1. 这是取价带，因为这里只有两条带，所以取第2条。如果哈密顿量是8x8的，能带可以取第5、6、7、8条，前提是要在排序后。

      回复

      2. 请问老师如果我是8X8的无自旋超导哈密顿量，一个原胞四个电子，四个空穴；电子掺杂浓度为2.12；doping0.12；那么还是取价带的四条能带算陈数吗，，

        回复

  20. 请问老师在matlab代码里的偏函数HH中，我新输入一个8X8的哈密顿，算出来陈数是-1.8514+0000i,这代表是拓扑平庸还是非平庸呢

    回复

    1. 可能哪里有问题吧，比如存在简并什么的。一般来说，算出来应该为整数。

      回复

  21. 暂且称呼您为关老师吧！
    关老师您好，我用您的高效法的matlab代码，设置n=500,算出的C=2.002638...，我看您用python设置n=100算出的C都比我精确，我算的是有什么问题吗？

    回复

    1. 我也不确定。如果逻辑都一样的话应该没有太大问题。之所以结果不一样，有可能是因为Matlab和Python计算特征向量时有不同的结果，恰巧一种算法得到的特征向量在后续的计算中更收敛。

      回复

  22. 高效法和定义法计算chern number，积分范围都是选取的(-pi,pi),不用对应格子的第一布里渊区吗？

    回复

    1. 这里的模型类似于方格子，第一布里渊区布的范围刚好是kx,ky为(-pi,pi)。如果是其他形式的，需要对布里渊区积分。

      回复

  23. 哈密顿量二次量后，矩阵就是所要表达的哈密顿量，直接代入就可？

    回复

      1. 明白了，谢谢。不过我用文献中方法计算chern number结果为0，正负1，正负2，但是用高效法计算结果一直为0（不论是否赋值）

        回复

  24. 博主在取离散kx,ky时，用的代码是 for kx in np.linspace(-pi, pi, n).

    这里用np.linspace给出的kx包括左右边界，会导致重复求和，因此得到的Chern number也精度也不高（例题主代码中n=1000，C=1.997...）。改成for kx in np.arange(-pi, pi, 2*pi/n) 的话，n很小就能得到正确结果（n=4得到C=2）。

    回复

    1. 感谢！用np.linspace是会存在多取点的问题，之前没关注到这个，代码已更新。

      回复

    1. HH(kx,ky)返回的是哈密顿量矩阵。如果你已知的是每个(kx，ky)对应的波函数，那么直接替换get_vector()就可以了。

      回复

  26. 您好博主，我想问一下，是否有类似的方法算出贝里联络，现在需要算贝里联络（还是2*2的矩阵），最后积分，请问有类似避开随机相位的方法么？

    回复

  27. 您好，请问下参考文献1公式（7）后面有一段话“ The link variables are well defined as long as N_mu neq 0, which can always be assumed to be the case (one can avoid a singularity N_mu = 0 by an infinitesimal shift of the lattice).”这里“an infinitesimal shift of the lattice”该如何理解？计算中又是怎么操作的了？

    回复

    1. 要求是分母不为零，这时候U才可以定义。如果在某些取值下，分母出现为零的情况，这时候可以稍微加一些微小量，例如1e-6，使得在数值上避开这个奇异点。目前我是没遇到这个情况，你如果有遇到这个情况，可以试试看这种处理方式。

      回复

  28. 您好，感谢分享，对我帮助很大。还想请教一个问题：我在MATLAB下使用这种高效法计算一个多能带体系的时候，发现本征矢矩阵中出现了很多零项，导致最后有些能带陈数为NaN。请问这可能是什么原因了？

    回复

    1. 本征矢为零？我也不清楚是什么原因导致的。可以试着看错误结果在每一行代码中的中间数据，找找什么是问题。

      回复

      1. 感谢回复。我思考了下，应该是我哈密顿量的结构问题，波戈留波夫哈密顿量类似于超导中电子空穴对的哈密顿量。在对角有两个互为共轭的block矩阵，逆对角线上是0，最后导致本征矢对应部分也是0。这种情况可能不能直接用高效法计算。

        回复

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

Captcha Code