陈数Chern number的计算（多条能带的Wilson loop方法，附Python代码）

这是之前的一篇：陈数Chern number的计算（Wilson loop方法，附Python代码），仅仅是计算某条能带的陈数，不支持能带交叉或简并。本篇给出支持能带交叉或简并的代码，即多带同时计算Wilson loop，并求行列式。公式和之前那篇博文一样：https://topocondmat.org/w4_haldane/ComputingChern.html。

为了验证算法和代码的正确性，这里以这篇文章为例子：方格子紧束缚模型中朗道能级的陈数/霍尔电导（附Python代码）。当Ny为偶数时，存在能带交叉的情况，这时候需要两条带同时计算才能给出正确的陈数结果。之前那篇已经给出计算能带的代码，这里代码略，本篇底部有直接贴上对应的能带图。

补充说明：Wilson loop方法计算结果之所以存在虚部，根本原因是因为Wilson loop之后没有除以归一化系数。如果考虑了归一化系数，就没有虚部，参考这篇中的公式：陈数Chern number的计算（高效法，附Python/Matlab代码），感谢Song MR同学参与的讨论。另外，微信公众号的这篇文章也给出了原因：https://mp.weixin.qq.com/s/Ci8FCjtj7I93PE5aHmgrzA。如果考虑了归一化系数，这里的表达式和高效法的表达式是完全一致的。个人推荐加上这个归一化系数。

代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/23989
"""

import numpy as np
import math
from math import *
import cmath
import functools

def hamiltonian(kx, ky, Ny, B):
    h00 = np.zeros((Ny, Ny), dtype=complex)
    h01 = np.zeros((Ny, Ny), dtype=complex)
    t = 1
    for iy in range(Ny-1):
        h00[iy, iy+1] = t
        h00[iy+1, iy] = t
    h00[Ny-1, 0] = t*cmath.exp(1j*ky)
    h00[0, Ny-1] = t*cmath.exp(-1j*ky)
    for iy in range(Ny):
        h01[iy, iy] = t*cmath.exp(-2*np.pi*1j*B*iy)
    matrix = h00 + h01*cmath.exp(1j*kx) + h01.transpose().conj()*cmath.exp(-1j*kx)
    return matrix


def main():
    Ny = 20

    H_k = functools.partial(hamiltonian, Ny=Ny, B=1/Ny)

    chern_number = calculate_chern_number_for_square_lattice_with_wilson_loop_for_degenerate_case(H_k, index_of_bands=range(int(Ny/2)-1), precision_of_wilson_loop=5)
    print('价带：', chern_number)
    print()

    chern_number = calculate_chern_number_for_square_lattice_with_wilson_loop_for_degenerate_case(H_k, index_of_bands=range(int(Ny/2)+2), precision_of_wilson_loop=5)
    print('价带（包含两个交叉能带）：', chern_number)
    print()

    chern_number = calculate_chern_number_for_square_lattice_with_wilson_loop_for_degenerate_case(H_k, index_of_bands=range(Ny), precision_of_wilson_loop=5)
    print('所有能带：', chern_number)

    # # 函数可通过Guan软件包调用。安装方法：pip install --upgrade guan
    # import guan
    # chern_number = guan.calculate_chern_number_for_square_lattice_with_wilson_loop_for_degenerate_case(hamiltonian_function, index_of_bands=[0, 1], precision_of_plaquettes=20, precision_of_wilson_loop=5, print_show=0)


def calculate_chern_number_for_square_lattice_with_wilson_loop_for_degenerate_case(hamiltonian_function, index_of_bands=[0, 1], precision_of_plaquettes=20, precision_of_wilson_loop=5, print_show=0):
    delta = 2*math.pi/precision_of_plaquettes
    chern_number = 0
    for kx in np.arange(-math.pi, math.pi, delta):
        if print_show == 1:
            print(kx)
        for ky in np.arange(-math.pi, math.pi, delta):
            vector_array = []
            # line_1
            for i0 in range(precision_of_wilson_loop):
                H_delta = hamiltonian_function(kx+delta/precision_of_wilson_loop*i0, ky) 
                eigenvalue, eigenvector = np.linalg.eig(H_delta)
                vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))]
                vector_array.append(vector_delta)
            # line_2
            for i0 in range(precision_of_wilson_loop):
                H_delta = hamiltonian_function(kx+delta, ky+delta/precision_of_wilson_loop*i0)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta)
                vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))]
                vector_array.append(vector_delta)
            # line_3
            for i0 in range(precision_of_wilson_loop):
                H_delta = hamiltonian_function(kx+delta-delta/precision_of_wilson_loop*i0, ky+delta)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta)
                vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))]
                vector_array.append(vector_delta)
            # line_4
            for i0 in range(precision_of_wilson_loop):
                H_delta = hamiltonian_function(kx, ky+delta-delta/precision_of_wilson_loop*i0)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta)
                vector_delta = eigenvector[:, np.argsort(np.real(eigenvalue))]
                vector_array.append(vector_delta)           
            wilson_loop = 1
            dim = len(index_of_bands)
            for i0 in range(len(vector_array)-1):
                dot_matrix = np.zeros((dim , dim), dtype=complex)
                i01 = 0
                for dim1 in index_of_bands:
                    i02 = 0
                    for dim2 in index_of_bands:
                        dot_matrix[i01, i02] = np.dot(vector_array[i0][:, dim1].transpose().conj(), vector_array[i0+1][:, dim2])
                        i02 += 1
                    i01 += 1
                det_value = np.linalg.det(dot_matrix)
                wilson_loop = wilson_loop*det_value
            dot_matrix_plus = np.zeros((dim , dim), dtype=complex)
            i01 = 0
            for dim1 in index_of_bands:
                i02 = 0
                for dim2 in index_of_bands:
                    dot_matrix_plus[i01, i02] = np.dot(vector_array[len(vector_array)-1][:, dim1].transpose().conj(), vector_array[0][:, dim2])
                    i02 += 1
                i01 += 1
            det_value = np.linalg.det(dot_matrix_plus)
            wilson_loop = wilson_loop*det_value
            arg = np.log(wilson_loop)/1j
            chern_number = chern_number + arg
    chern_number = chern_number/(2*math.pi)
    return chern_number


if __name__ == '__main__':
    main()

运算结果：

价带： (-8.999999999999996+22.620063283010385j)

价带（包含两个交叉能带）： (8.000000000000004+22.225601922823458j)

所有能带： (8.988228160493337e-16+4.549167968104345j)

当增加precision_of_wilson_loop值时，虚数会变小。这里似乎对实部结果没影响。推荐使用这篇文章中的方法：陈数Chern number的计算（多条能带的高效法，附Python代码），即考虑了归一化系数。

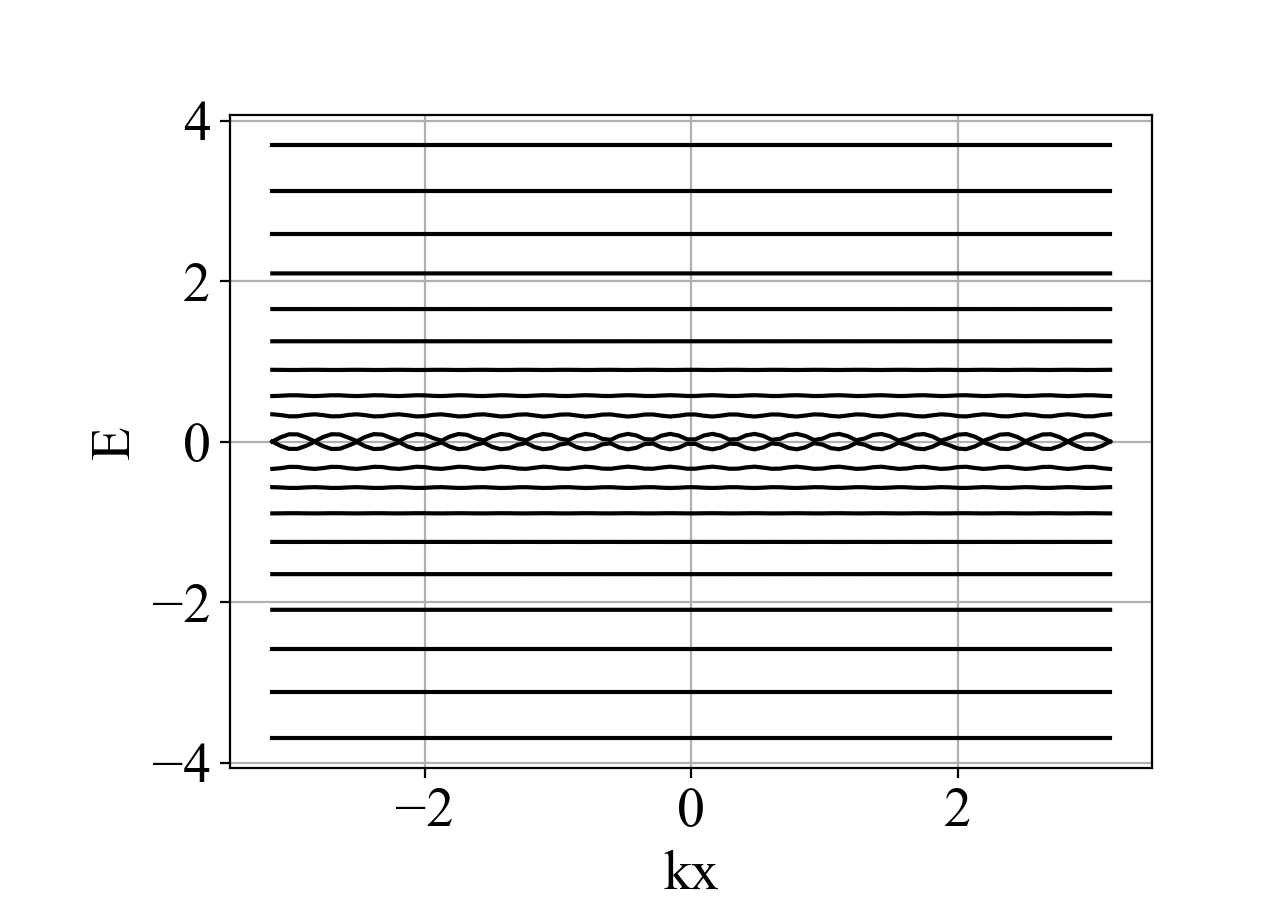
以上计算对应的能带图：

3,134 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】