贝里相位、贝里联络、贝里曲率和陈数

本篇推导贝里相位 $\phi$ 、贝里联络 $\bm{A}$ 、贝里曲率 $\bm{\Omega}$ 和陈数 $C$ 之间的关系。

贝里相位的定义（离散的情况是写成Wilson loop的形式）：

$\phi = -\mathrm{Im} \ \mathrm{ln}\big[\langle u_0|u_1 \rangle \langle u_1|u_2 \rangle ... \langle u_{N-1}|u_0 \rangle \big]$

通过以下变换[2]，

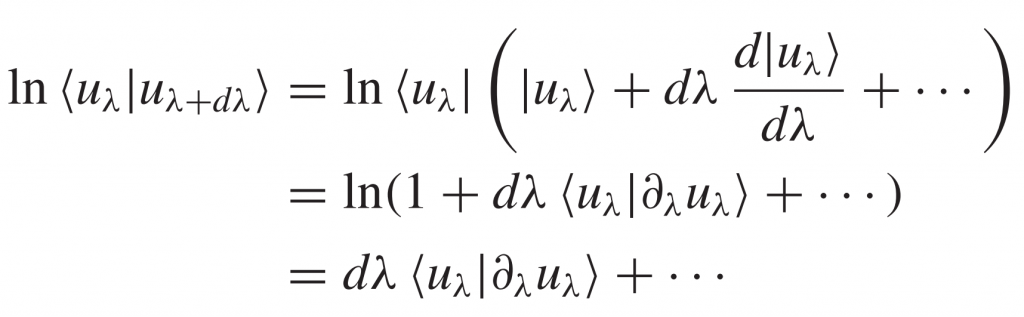
可以得到连续的形式：

$\phi=\oint \langle u_{\lambda}|i \partial_{\lambda} u_{\lambda} \rangle d\lambda$

其中，贝里联络定义为：

$\bm{A}(\lambda)=\langle u_{\lambda}|i \partial_{\lambda} u_{\lambda} \rangle$

贝里曲率定义为：

$\bm{\Omega}(\lambda) = \bm{\nabla}_{\lambda} \times \bm{A}(\lambda)$

由格林公式或斯托克斯公式，可以知道贝里相位的环路积分等价于贝里曲率的面积分。

$\int_S \bm{\Omega} (\lambda)d \bm{S} = \oint_P \bm{A} \cdot d \bm{\lambda}$

需要注意的是：以上等式的成立是需要条件的，即波函数在整个S面上要光滑连续。

根据陈定理（Chern theorem），等式左边对布里渊区（封闭的二维流形）积分恒等于 $2\pi n$ ，其中 $n$ 为整数（陈数），即 $\oint_S \bm{\Omega} (\lambda)d \bm{S} = 2\pi n$ 。

如果波函数在整个封闭流形上是光滑连续的，那么把这个封闭的流形分成A,B两个区域，分别用上Stokes定理： $\int_A \bm{\Omega} (\lambda)d \bm{S} =\phi$ 和 $\int_B \bm{\Omega} (\lambda)d \bm{S} =-\phi$ ，其中 $\phi$ 和 $-\phi$ 分别是A,B区域的贝里相位（沿着A,B区域的路径P积分）。于是，对整个封闭的流形积分有： $\oint_S \bm{\Omega} (\lambda)d \bm{S}=\int_A \bm{\Omega} (\lambda)d \bm{S}+\int_B \bm{\Omega} (\lambda)d \bm{S}=0$ ，即陈数为0。

因此[1]：

陈数在数学上的意义是[1-6]：

A nonzero Chern index presents a topological obstruction to the construction of a globally smooth gauge.

附：格林公式和斯托克斯公式[7]

（1）格林（Green）公式

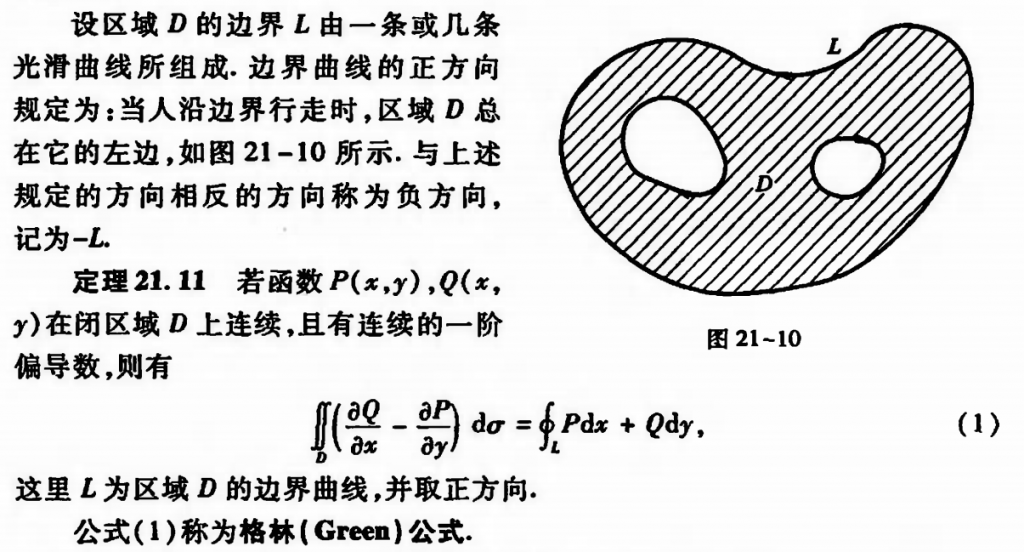
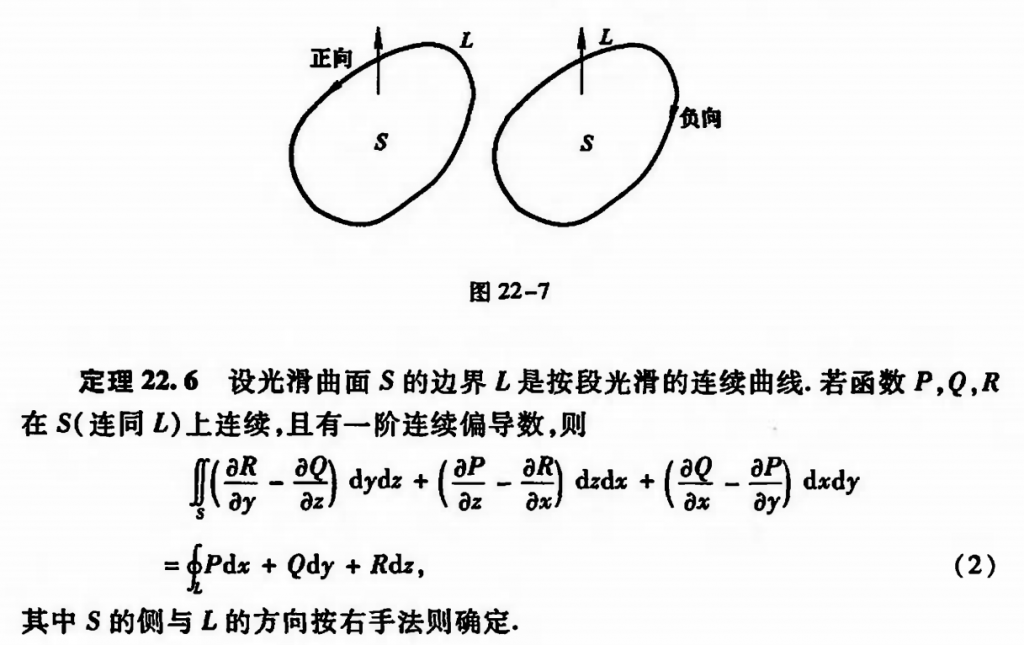
（2）斯托克斯（Stokes）公式

参考资料：

[1] David Vanderbilt - Berry Phases in Electronic Structure Theory_ Electric Polarization, Orbital Magnetization and Topological Insulators (2018, Cambridge University Press)

[2] B. Andrei Bernevig - Topological Insulators and Topological Superconductors 第30页

[3] Berry phase effects on electronic properties (Di Xiao, Ming-Che Chang, and Qian Niu)

[4] 浅谈Berry相位（一）——基本概念

[5] 数学上陈数（Chern number）或 Berry Phase 有何意义？

[6] https://topocondmat.org/w4_haldane/ComputingChern.html

[7] 《数学分析》下册，华东师范大学数学系编，高等教育出版社

8,220 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

10 thoughts on “贝里相位、贝里联络、贝里曲率和陈数”

老师您好。我得到一个能带在二维布里渊区中的本征向量丛，用文中的公式导出贝利曲率在布里渊区上的分布，它虚部并不是零，反而比实部还大一些（在您给我们展示的石墨烯的例子中，它的虚部是接近0的，只有一点数值误差）。因此我想知道“贝利曲率是实数”是怎么来的，如果用文中的公式导出的贝利曲率实部虚部都不接近零，这个虚部的物理意义是什么？

guanjihuan说道：

2024年6月17日 18:00

我的理解是贝里曲率应该要为实数的，这里给出证明，供参考：贝里曲率为实数的证明。可以检查下相邻波函数是否是连续的，以及k点是否取得足够近。

回复
1. 匿名说道：
  
  2024年6月17日 20:17
  
  感谢！也就是说贝利曲率虚部为0的条件是本征向量丛是个每个向量都归一化的复向量丛，如果本征向量在参数空间中长度分布不一致，就产生了贝利联络的非零虚部，但那是没意义的（本征向量乘任意常数还是它本身）。这样理解正确吧？
  
  回复
  1. guanjihuan说道：
    
    2024年6月17日 21:01
    
    嗯，数学上可能会有复数的情况，这个我不大了解。在物理上，波函数相邻k点一般是连续的，以及波函数需要归一化（量子力学的基本性质），所以贝里曲率为实数。其实也比较好理解，因为贝里曲率是倒空间的“磁场”，如果为复数会有点奇怪，另外，它在布里渊区的积分也要为整数。
    
    你说的向量长度应该没什么关系，即使不是1，是其他长度，求导也是0，同样有一样的证明结果。
    
    回复

这里贝里相位的离散定义为啥有负号呢？正负号有影响吗

guanjihuan说道：

2024年3月8日 11:35

定义就是这个。这里的负号+取虚部，等效于连续形式中的*i。

回复

“贝里相位的环路积分等价于贝里曲率的面积分”，那里写错吗？贝里联络的环路积分等价于贝里曲率的面积分？

guanjihuan说道：

2023年10月12日 16:41

是有前提条件的。如果陈数为零是成立的，如果陈数不为零则不成立。

回复

请问最开始推导Berry相位的连续形式时，第三个等号后ln为什么可以直接摘掉呀？

guanjihuan说道：

2022年9月26日 16:36

ln(1+x)的泰勒展开近似，只取第一项。

回复

贝里相位、贝里联络、贝里曲率和陈数

Published by guanjihuan

10 thoughts on “贝里相位、贝里联络、贝里曲率和陈数”

发表评论取消回复

Published by guanjihuan

10 thoughts on “贝里相位、贝里联络、贝里曲率和陈数”

发表评论 取消回复

发表评论取消回复