实空间拓扑不变量（local Chern marker）的Python代码实现例子

这个是之前的一篇：一个实空间拓扑不变量的公式推导（local Chern marker），本篇给出具体的Python代码实现，以 half BHZ 模型为例。BHZ 模型可以参考之前的这篇：BHZ模型哈密顿量与准一维体系的能带图（附Python代码）。

本篇代码中用到 GUAN 软件包：https://py.guanjihuan.com。

实现代码如下：

import numpy as np
import guan


# 计算投影算符
def compute_projection_operator(Ny, Nx):
    H0, H1, H2 = guan.get_onsite_and_hopping_terms_of_half_bhz_model_for_spin_down(A=0.3645/5, B=-0.686/25, C=0, D=-0.512/25, M=-0.01, a=1)
    hamiltonian = guan.hamiltonian_of_finite_size_system_along_two_directions_for_square_lattice(N1=Ny, N2=Nx, on_site=H0, hopping_1=H1, hopping_2=H2, period_1=0, period_2=0)

    P = np.zeros((2*Ny*Nx, 2*Ny*Nx), dtype=complex)
    eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
    occupied = 0
    for i0 in eigenvalue:
        if i0 <= 0:
            occupied += 1
    for i0 in range(occupied):
        P += np.outer(eigenvector[:, i0], eigenvector[:, i0].conj())
    
    return P


# 计算local Chern marker
def compute_local_chern_marker(Ny, Nx, P):
    C_local = np.zeros((Ny, Nx), dtype=complex)
    x_array = np.zeros((2*Ny*Nx))
    y_array = np.zeros((2*Ny*Nx))
    for iy in range(Ny):
        for ix in range(Nx):
            x_array[2*Nx*iy + 2*ix + 0] = ix
            x_array[2*Nx*iy + 2*ix + 1] = ix
            y_array[2*Nx*iy + 2*ix + 0] = iy
            y_array[2*Nx*iy + 2*ix + 1] = iy
    x_matrix = np.diag(x_array)   
    y_matrix = np.diag(y_array) 

    PxP = P @ x_matrix @ P
    PyP = P @ y_matrix @ P
    commutator = PxP @ PyP - PyP @ PxP
    for iy in range(Ny):
        for ix in range(Nx):
            C_local[iy, ix] = -2 * np.pi * 1j * (commutator[2*Nx*iy+ 2*ix + 0, 2*Nx*iy+ 2*ix + 0] + commutator[2*Nx*iy+ 2*ix + 1, 2*Nx*iy+ 2*ix + 1])

    # # 或者用这个
    # temp = 4 * np.pi * np.imag(P @ x_matrix @ P @ y_matrix @ P)
    # for iy in range(Ny):
    #     for ix in range(Nx):
    #         C_local[iy, ix] = temp[2*Nx*iy + 2*ix + 0, 2*Nx*iy + 2*ix + 0] + temp[2*Nx*iy + 2*ix + 1, 2*Nx*iy + 2*ix + 1]

    return C_local.real


Nx=30
Ny=30
P = compute_projection_operator(Ny, Nx)
C_local = compute_local_chern_marker(Ny, Nx, P)
guan.plot_pcolor(range(Nx), range(Ny), C_local, cmap='RdBu')

运行结果：

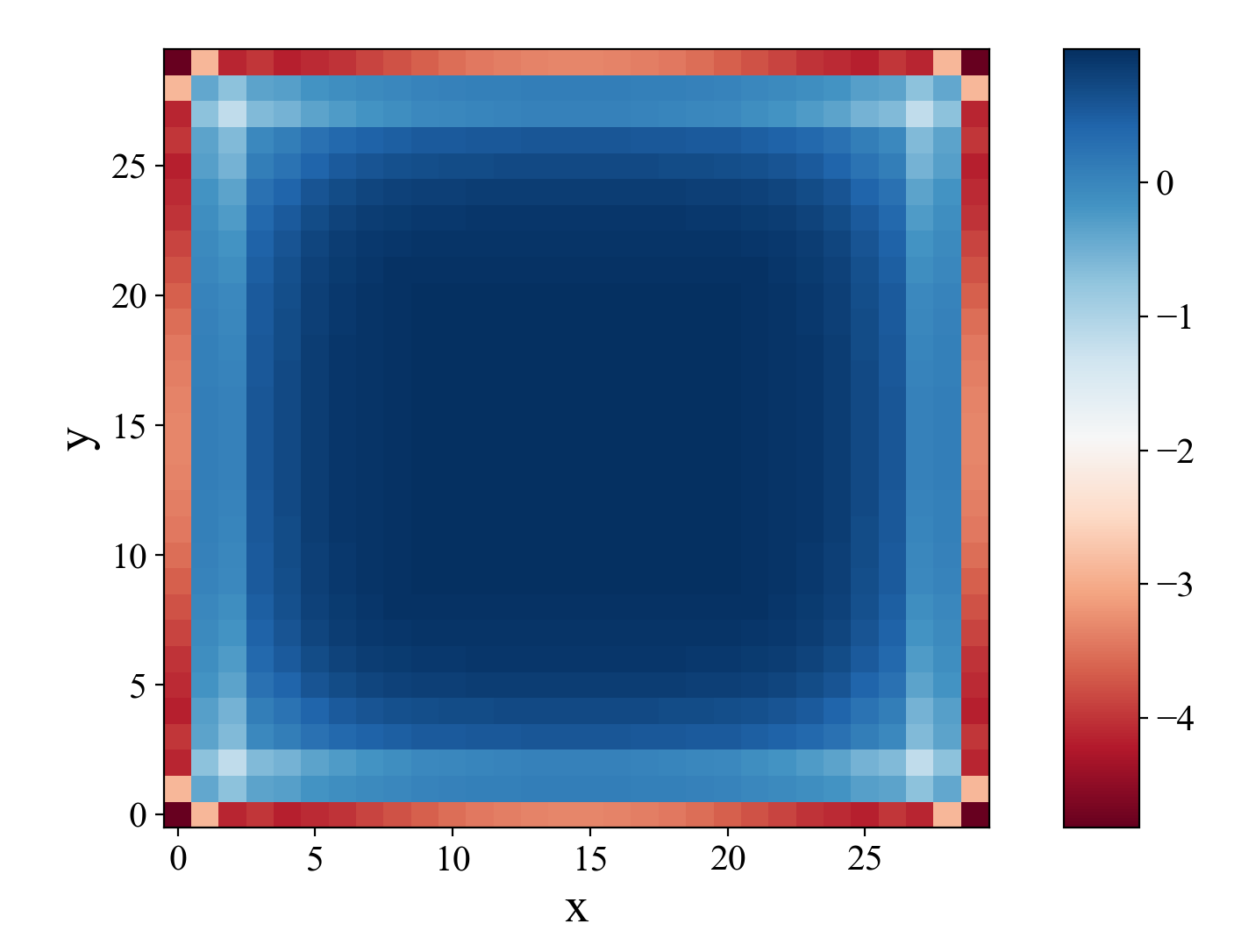
参考资料：

[1] Mapping topological order in coordinate space

[2] Localization trajectory and Chern-Simons axion coupling for bilayer quantum anomalous Hall systems

[3] Current carrying states in the disordered quantum anomalous Hall effect

[4] Topological Hofstadter insulators in a two-dimensional quasicrystal

[5] Topological marker currents in Chern insulators

[6] Local Chern marker of smoothly confined Hofstadter fermions

[7] Layer Hall effect induced by hidden Berry curvature in antiferromagnetic insulators

409 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】