模型和能带, 学术

石墨烯紧束缚模型到低能有效模型的推导

发布时间：2021年3月27日2022年11月21日

最近修改时间：2022年11月21日

1. 石墨烯紧束缚模型

这是之前的两篇：

石墨烯示意图为[1]：

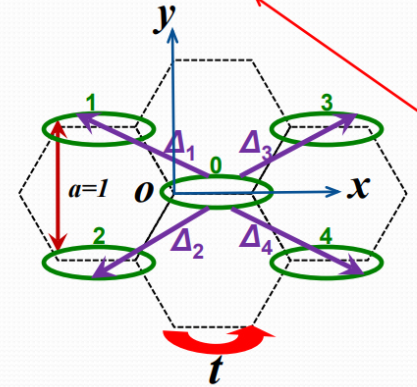
石墨烯紧束缚模型在倒空间的形式（晶格常数为1，原子间距为 $1/\sqrt{3}$ ）：

$H=\sum_{k} \begin{pmatrix}|\mathbf{k}, A\rangle |\mathbf{k}, B\rangle\end{pmatrix}\begin{pmatrix}0 & f(\mathbf{k})\\f^{*}(\mathbf{k}) & 0\end{pmatrix}\begin{pmatrix}\langle \mathbf{k}, A| \\\langle \mathbf{k}, B|\end{pmatrix}$

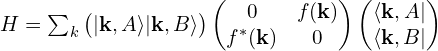
其中， $f(\mathbf{k})=1+\mathrm{exp}(-\frac{\sqrt{3}i}{2}k_x+\frac{i}{2}k_y)}+\mathrm{exp}(-\frac{\sqrt{3}i}{2}k_x-\frac{i}{2}k_y)}$

以上的表达式是以元胞为单元进行的傅里叶变换[2,3]。如果以原子为单元， $f(\mathbf{k})$ 的表达式写为：

$f(\mathbf{k})=\mathrm{exp}(\frac{i}{\sqrt{3}}k_x)+\mathrm{exp}(-\frac{i}{2\sqrt{3}}k_x+\frac{i}{2}k_y)}+\mathrm{exp}(-\frac{i}{2\sqrt{3}}k_x-\frac{i}{2}k_y)}$

2. 石墨烯低能有效模型

接着把石墨烯紧束缚模型在狄拉克点附近展开，可以得到狄拉克点附近的低能有效模型[1]。

石墨烯倒格子示意图为[1]：

找到两个狄拉克点的位置，为 $\mathbf{K}=(0, \frac{4}{3}\pi)$ 和 $\mathbf{K}'=(0, -\frac{4}{3}\pi)$ 。

以 $\mathbf{K}$ 谷为例，定义 $\mathbf{q}=\mathbf{k}-\mathbf{K}$ ，在 $\mathbf{q}=0$ 附近泰勒展开。参考"常用的泰勒近似"中的二元函数泰勒展开。

对表达式 $f(\mathbf{k})=1+\mathrm{exp}(-\frac{\sqrt{3}i}{2}k_x+\frac{i}{2}k_y)}+\mathrm{exp}(-\frac{\sqrt{3}i}{2}k_x-\frac{i}{2}k_y)}$ 泰勒展开：

$\begin{aligned} f(\mathbf{k}) &\approx f(\mathbf{K})+q_x \frac{\partial}{\partial k_x}f(\mathbf{K})+q_y \frac{\partial}{\partial k_y}f(\mathbf{K})\\&=0+q_x[-\frac{\sqrt{3}i}{2}\mathrm{exp}(\frac{i}{2}\frac{4}{3}\pi)-\frac{\sqrt{3}i}{2}\mathrm{exp}(-\frac{i}{2}\frac{4}{3}\pi) ]\\& \quad \quad +q_y[\frac{i}{2}\mathrm{exp}(\frac{i}{2}\frac{4}{3}\pi)-\frac{i}{2}\mathrm{exp}(-\frac{i}{2}\frac{4}{3}\pi) ]\\&=\frac{\sqrt{3}i}{2}q_x-\frac{\sqrt{3}}{2}q_y\end{aligned}$

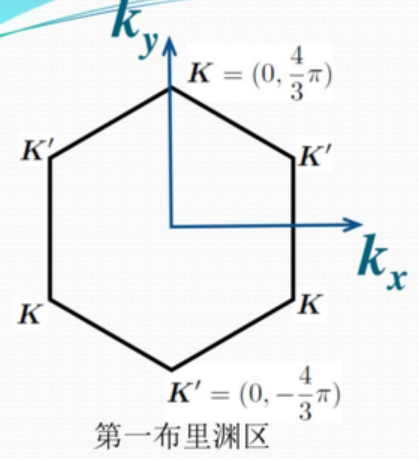
所以石墨烯的低能有效模型为[1]:

如果考虑 $\mathbf{K'}$ 谷，有

$f(k)\approx \frac{\sqrt{3}i}{2}q_x+\frac{\sqrt{3}}{2}q_y$

有效模型为：

$\frac{\sqrt{3}}{2} \begin{pmatrix} 0 & q_x i + q_y \\ -q_x i + q_y & 0 \end{pmatrix}=-\frac{\sqrt{3}}{2} (q_x \sigma_y - q_y \sigma_x)$

参考资料：

[1] 广州大学Prof. Yanyang Zhang的课件

[2] 离散格子的傅里叶变换和反傅里叶变换

[3] 知乎：六角蜂窝格子紧束缚模型的计算

9,107 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

7 thoughts on “石墨烯紧束缚模型到低能有效模型的推导”

陶争说道：

2025年4月14日 20:39

博主，您好，对于转角石墨烯的能带我有一点疑惑，我使用紧束缚模型计算能带，考虑到4a_0作为截止距离，计算出的能带中间的分界线不是零，这是否正常？

回复
1. guanjihuan说道：
  
  2025年4月15日 00:04
  
  具体情况我不清楚，能带中间的分界线是不是零可能和对称性有关系。判断结果对不对可以多做代码检查，以及适当把模型简化看是否会回到简单模型的计算结果。如果有相关文献，也可以和文献中的图做对比。
  
  回复
匿名说道：

2023年3月21日 21:05

博主，你好！在您给的参考资料里，a+iaj表示从i到j的跃迁，不明白的是，a+i是在i产生一个电子，aj是湮灭一个电子，a+iaj不应该是从j到i的跃迁吗

回复
1. guanjihuan说道：
  
  2023年3月21日 23:06
  
  嗯，你理解的应该是对的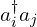， $a^{\dagger}_{i} a_{j}$ 是从j到i的跃迁。别处可能是笔误吧，而且对厄米系统来说也无关紧要，是厄米对称的。
  
  回复
匿名说道：

2021年9月2日 15:48

博主您好，狄拉克点在三维空间一般是四重简并的，但是这是算的是2*2矩阵，得到的是两能带图，这表现不出来它的四重简并啊？

回复
1. guanjihuan说道：
  
  2021年9月2日 22:09
  
  这里考虑的哈密顿量是没有自旋的（spinless）。如果考虑了自旋，就是四重简并。
  参考资料：
  [1] https://mattermodeling.stackexchange.com/questions/1704/weyl-semimetal-and-dirac-semimetal/1826
  [2] https://mattermodeling.stackexchange.com/questions/1598/how-to-understand-the-time-reversal-symmetry-in-graphene/1602
  
  回复
  1. 匿名说道：
    
    2021年9月3日 14:53
    
    谢谢，一直有这个疑问
    
    回复

发表评论取消回复