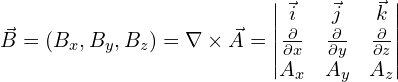
采用朗道规范（Landau gauge），方法如下：
（1）当
时，磁势可选为：
或 
（2） 当
时，磁势可选为：
或 
（3） 当
时，磁势可选为：
或 
参考资料：
[1] 点乘a*b和叉乘aXb
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
磁场和磁势的选取
欢迎访问我的个人网站
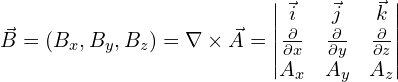
采用朗道规范（Landau gauge），方法如下：
（1）当时，磁势可选为：
或
（2） 当时，磁势可选为：
或
（3） 当时，磁势可选为：
或
参考资料：
[1] 点乘a*b和叉乘aXb
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
请问，如果用三角格子加y方向磁场，用两点之间的距离公式x-x1/x2-x1=z-z1/z2-z1,和朗道规范（Bz,0,0),求2Πi/Φ∫Bzdx，等于Πi/ΦB（z1+z2)(x1-x2)，双层材料可以设z1为0,直接在上层的跃迁上加相位吗。
应该是可以的，z 坐标没有严格定义，取哪个位置为 0 都可以。通过测试应该可以看到，z1 取任意值，对可观测物理量的计算结果是不会有影响的。
请问如果在两层之间加水平磁场，方格子怎么加啊那个z方向的积分体现在哪一项啊
看取的规范吧，如果磁势的 z 分量为零，那就是没有。
如果选A=（0，0，yB)的话，用三角格子计算，假设底层z为0，跃迁项是加在层间耦合项大小是2Πi/ϕ*yBz吗
嗯，我不确定，具体大小可以参考：佩尔斯替换 Peierls substitution。