本篇内容主要参考国科大金彪老师“高等量子力学”手稿课件。
一、纯态
1. 纯态:![]() (可以是本征态,也可以是叠加态)
(可以是本征态,也可以是叠加态)
2. 纯态密度算符:![]()
3. 算符![]() 的平均值:
的平均值:
![Rendered by QuickLaTeX.com \begin{aligned}\langle\hat{B}\rangle&=\langle \psi(t)| \hat{B} |\psi(t) \rangle\\&=\sum_{n}\langle \psi(t)| \hat{B} | a_n\rangle \langle a_n |\psi(t) \rangle\\&=\sum_{n} \langle a_n |\psi(t) \rangle \langle \psi(t)| \hat{B} | a_n\rangle\\&=\sum_{n} \langle a_n |\hat{\rho}(t)\hat{B}|a_n \rangle \\&=\mathrm{Tr}[\hat{\rho}(t)\hat{B}]\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-94286675c19d73d5892faac8adb8ae75_l3.png)
4. 性质:![]() ,证明:
,证明:
![Rendered by QuickLaTeX.com \begin{aligned}\mathrm{Tr}[\hat{\rho}(t)]&=\sum_n \langle a_{n}|\hat{\rho}(t)|a_n\rangle \\&=\sum_n \langle a_{n}|\psi(t)\rangle \langle \psi(t)|a_n\rangle\\&=\langle \psi(t)|a_n\rangle \langle a_{n}|\psi(t)\rangle\\&=\langle \psi(t) | \psi(t) \rangle =1\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-ff43959c0d4db0cfe8196e746fffe4c3_l3.png)
5. 性质:![]() ,证明:
,证明:
![]()
二、混合态
1. 混合态中的参与态:![]() ,
, ![]() , ...,
, ..., ![]() ;权重:
;权重:![]() ,
, ![]() , ...,
, ..., ![]() 。
。
2. 混合态密度算符:![]()
3. 算符![]() 的平均值:
的平均值:![]() ,和纯态相同。证明过程类似,略。
,和纯态相同。证明过程类似,略。
4. 性质:![]() ,和纯态相同。证明过程类似,略。
,和纯态相同。证明过程类似,略。
5. 性质:![]() ,证明:
,证明:
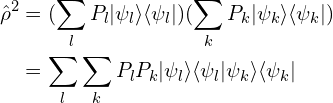
以![]() 的情况为例子:
的情况为例子:![]()
6. 性质:![]() 。
。
证明略。在证明过程中要用到Schwartz不等式:![]() 。
。
7. 需要强调的是:叠加态是纯态,不是混合态。混合态的概念稍微比较不好理解,在之后的纠缠态约化密度矩阵那边会用到混合态的概念。
三、纯态和混合态的例子
1. 纯态:![]()
纯态密度算符:
![]()
密度矩阵:
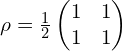
显然有:![]() ;
;![]() ;
;![]() 。
。
2. 混合态:参与态![]() ,
,![]() ;权重
;权重![]() ,
, ![]() 。
。
混合态密度算符:
![]()
密度矩阵:
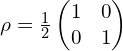
显然有:![]() ;
;![]() ;
;![]() ;
;![]() 。
。
四、复合系统
1. 复合系统的基矢量由直积(张量积)构成:![]() ,维度为
,维度为![]() 维。
维。
2. 基矢量的内积:![]()
3. 基矢量的正交性:![]()
4. 基矢量的完备性:![]()
5. 部分内积:![]()
6. 外积:![]()
7. 复合系统的算符:![]()
![]()
8. 算符![]() 在直积空间中的表示:
在直积空间中的表示:![]() ,其中
,其中![]() 为第二子空间的单位算符。类似:
为第二子空间的单位算符。类似:![]()
9. 复合系统的态矢量(纯态):
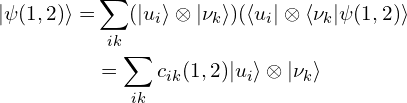
10. 归一性:![]()
11. 密度算符:![]()
12. 约化密度算符:略
五、纠缠态
![]() 可分成两大类:
可分成两大类:
1. 可分离态:![]() ,即:
,即:![]()
2. 纠缠态:![]()
判断![]() 是可分离态还是纠缠态,需要考察约化密度矩阵是否是混合态密度矩阵。具体内容略。
是可分离态还是纠缠态,需要考察约化密度矩阵是否是混合态密度矩阵。具体内容略。
六、纠缠态的例子
Bell基:
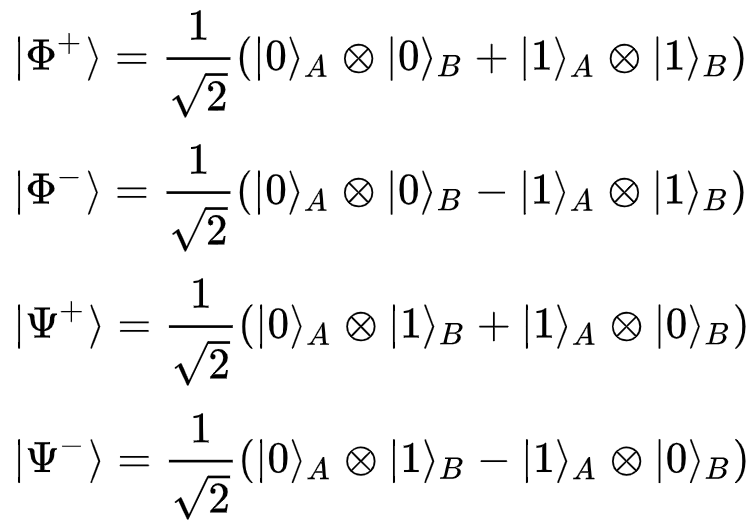
更多参考:
[1] 关于纯态、混合态的个人理解
[3] Quantum entanglement - Wikipedia
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
我想问问纠缠态就一定是纯态吗?我看到有的地方说对于纠缠态整体而言是纯态,而其子系统可以是混合态。有的地方又说纠缠态可以分为纠缠纯态和纠缠混态。这个问题我想不明白
对于完全分离的独立的系统,“纠缠态整体而言是纯态,而其子系统可以是混合态”这句话是对的,纠缠态子系统的约化密度矩阵为混合态。
你说的“纠缠纯态和纠缠混态”的概念我不是很熟悉,没怎么了解,可以看看教科书或文献中怎么定义。我猜区别可能是指这个纠缠态是否和其他子系统有发生纠缠,没有和其他子系统发生纠缠的是纠缠纯态,有和其他子系统发生纠缠的是纠缠混态?我这个理解不一定对,供参考。