第二类外尔半金属最小模型的能带图（附Python代码）

之前关于外尔半金属的博文：

这里讲第二类外尔半金属。当外尔锥（Weyl cone）倾斜到锥边越过外尔点所在的费米面，这类的外尔半金属称为第二类外尔半金属（Type-II Weyl semimetal）。第二类外尔半金属具有和第一类外尔半金属不一样的性质，具体可阅读相关文献。本篇给出最小模型的有效哈密顿量，并画出能带图。

具有倾斜锥的外尔半金属（Tilted Weyl Semimetal）哈密顿量[1,2,3]：

$H_{\mathrm{Weyl}}=\mathbf{w_{0}}\cdot \mathbf{k} \sigma_{0}+\sum_{i=1,2,3}v_{i}k_{i} \sigma_{i}$

其中，第一项是倾斜项，对应的 $\mathbf{w_{0}}$ 称为倾斜速度（the tilt velocity）。第二项是外尔半金属的一般形式， $v_i$ 表示各项异性的费米速度（anisotropic Fermi velocities）。

该模型也可以写成更一般的形式[4,5,6]：

$H_{\mathrm{Weyl}}=\mathbf{w_{0}}\cdot \mathbf{k} \sigma_{0}+\sum_{i,j=1,2,3}v_{ij}k_{i} \sigma_{j}$

这里考虑前面那个最简单的形式，求本征值得到：

$\begin{aligned}E&=\mathbf{w_{0}}\cdot \mathbf{k} \pm \sqrt{v_{x}^{2}k_{x}^{2}+v_{y}^{2}k_{y}^{2}+v_{z}^{2}k_{z}^{2}}\\&=w_{0x}k_x + w_{0y}k_y + w_{0z}k_z \pm \sqrt{v_{x}^{2}k_{x}^{2}+v_{y}^{2}k_{y}^{2}+v_{z}^{2}k_{z}^{2}}\\&=T(\mathbf{k}) \pm U(\mathbf{k})\end{aligned}$

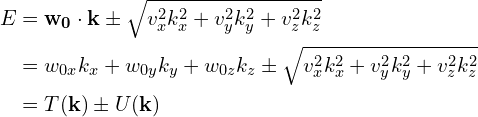
第二类外尔半金属的定义[5,6]：在布里渊区内存在一个方向 $\mathbf{e_k}$ ，使得

$T(\mathbf{e_k})>U(\mathbf{e_k})$

（1）第二类外尔半金属能带

当 $w_{0x} = 2, w_{0y} = 0, w_{0z} = 0, v_x = 1, v_y = 1, v_z = 1$ 时，模型为第二类外尔半金属。Python代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/10385
"""

import numpy as np
from math import *


def main():
    k1 = np.linspace(-pi, pi, 100)
    k2 = np.linspace(-pi, pi, 100)

    eigenvalue_array = Calculate_Eigenvalue_with_Two_Parameters(k1, k2, hamiltonian)
    Plot_3D_Surface(k1, k2, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', title='', filename='a')


def hamiltonian(kx,ky,kz=0):
    w0x = 2
    w0y = 0
    w0z = 0
    vx = 1
    vy = 1
    vz = 1
    H = (w0x*kx+w0y*ky+w0z*kz)*sigma_0() + vx*kx*sigma_x()+vy*ky*sigma_y()+vz*kz*sigma_z()
    return H


def sigma_0():
    return np.eye(2)

def sigma_x():
    return np.array([[0, 1],[1, 0]])


def sigma_y():
    return np.array([[0, -1j],[1j, 0]])


def sigma_z():
    return np.array([[1, 0],[0, -1]])


def Calculate_Eigenvalue_with_Two_Parameters(x, y, matrix):  
    dim = np.array(matrix(0, 0)).shape[0]
    dim_x = np.array(x).shape[0]
    dim_y = np.array(y).shape[0]
    eigenvalue_array = np.zeros((dim_y, dim_x, dim))
    i0 = 0
    for y0 in y:
        j0 = 0
        for x0 in x:
            matrix0 = matrix(x0, y0)
            eigenvalue, eigenvector = np.linalg.eig(matrix0)
            eigenvalue_array[i0, j0, :] = np.sort(np.real(eigenvalue[:]))
            j0 += 1
        i0 += 1
    return eigenvalue_array


def Plot_3D_Surface(x, y, matrix, xlabel='x', ylabel='y', zlabel='z', title='', filename='a'): 
    import matplotlib.pyplot as plt
    from matplotlib import cm
    from matplotlib.ticker import LinearLocator
    fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
    plt.subplots_adjust(bottom=0.1, right=0.8) 
    x, y = np.meshgrid(x, y)
    if len(matrix.shape) == 2:
        surf = ax.plot_surface(x, y, matrix, cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    elif len(matrix.shape) == 3:
        for i0 in range(matrix.shape[2]):
            surf = ax.plot_surface(x, y, matrix[:,:,i0], cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    ax.set_title(title, fontsize=20, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=20, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=20, fontfamily='Times New Roman') 
    ax.set_zlabel(zlabel, fontsize=20, fontfamily='Times New Roman') 
    # ax.set_zlim(-1, 1)  # 设置z轴的范围
    ax.zaxis.set_major_locator(LinearLocator(5)) # 设置z轴主刻度的个数
    ax.zaxis.set_major_formatter('{x:.2f}')   # 设置z轴主刻度的格式
    ax.tick_params(labelsize=15)  # 设置刻度值字体大小
    labels = ax.get_xticklabels() + ax.get_yticklabels() + ax.get_zticklabels()
    [label.set_fontname('Times New Roman') for label in labels] # 设置刻度值字体
    # plt.savefig(filename+'.jpg', dpi=300) 
    plt.show()
    plt.close('all')


if __name__ == '__main__':
    main()

运行结果：

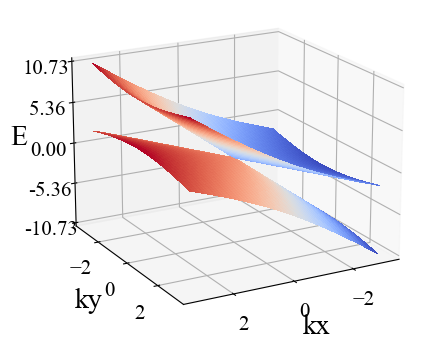
（2）临界的情况：

def hamiltonian(kx,ky,kz=0):
    w0x = 1
    w0y = 0
    w0z = 0
    vx = 1
    vy = 1
    vz = 1
    H = (w0x*kx+w0y*ky+w0z*kz)*sigma_0() + vx*kx*sigma_x()+vy*ky*sigma_y()+vz*kz*sigma_z()
    return H

运行结果：

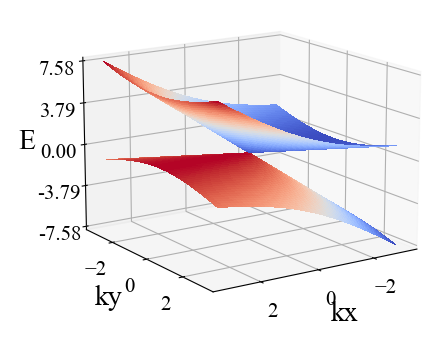
（3）第一类外尔半金属（完全不倾斜的情况）：

def hamiltonian(kx,ky,kz=0):
    w0x = 0
    w0y = 0
    w0z = 0
    vx = 1
    vy = 1
    vz = 1
    H = (w0x*kx+w0y*ky+w0z*kz)*sigma_0() + vx*kx*sigma_x()+vy*ky*sigma_y()+vz*kz*sigma_z()
    return H

运行结果：

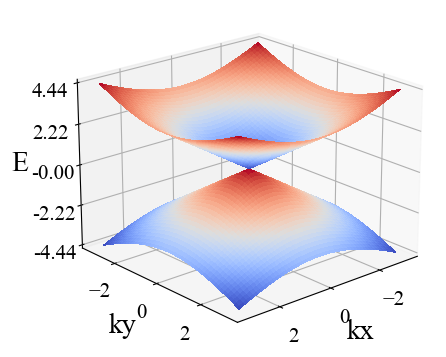
参考资料：

[1] Tilted anisotropic Dirac cones in quinoid-type graphene and α-(BEDT-TTF)2I3

[2] Magnetic-Field-Induced Relativistic Properties in Type-I and Type-II Weyl Semimetals

[3] Predicted Unusual Magnetoresponse in Type-II Weyl Semimetals

[4] Field-Selective Anomaly and Chiral Mode Reversal in Type-II Weyl Materials

[5] Minimal models for topological Weyl semimetals

[6] Type-II Weyl semimetals

[7] 更多相关的文献

2,384 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

2 thoughts on “第二类外尔半金属最小模型的能带图（附Python代码）”

zhangjiayan说道：

2021年7月4日 11:43

大佬您好，我如果想画上述体系的一维条带，我把这个k空间的哈密顿量化为实空间立方格子后，请问原胞该如何选择啊？另外您能看一下我的做法有什么问题吗？
我的做法是：实空间中，设输运方向延x方向，设y方向有400个格点，我取的原胞是沿着y方向的一个条，也就是y方向的400个格点是一个原胞，然后h00表示原胞间的hopping，h01是沿着x方向的hopping，然后利用h(k)=h00+h01*exp(ik)+h01'*exp(-ik)。我的一个疑问就是，我算能带的时候并没有加入沿着z方向的hopping矩阵，然后无论加不加z方向的hopping，画出的能带和论文的能带都对不上(大哭)，我在想，是不是我的原胞选的有问题啊？我是不是要选择沿着x方向的一个截面作为原胞啊(y-z面)？

回复
1. guanjihuan说道：
  
  2021年7月6日 03:23
  
  选取截面，x方向上最小重复单元。
  
  回复

第二类外尔半金属最小模型的能带图（附Python代码）

（1）第二类外尔半金属能带

（2）临界的情况：

（3）第一类外尔半金属（完全不倾斜的情况）：

Published by guanjihuan

2 thoughts on “第二类外尔半金属最小模型的能带图（附Python代码）”

发表评论取消回复

（1）第二类外尔半金属能带

（2）临界的情况：

（3）第一类外尔半金属（完全不倾斜的情况）：

Published by guanjihuan

2 thoughts on “第二类外尔半金属最小模型的能带图（附Python代码）”

发表评论 取消回复

发表评论取消回复