这里根据网上信息以及通过 AI 对话直接给出结论:
- 矩阵乘积:时间复杂度为
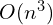
- 矩阵求逆:时间复杂度为
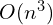
- 矩阵本征值:时间复杂度为
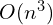
Python 代码验证:
import numpy as np
import matplotlib.pyplot as plt
import time
time_1 = np.array([])
time_2 = np.array([])
time_3 = np.array([])
n_all = np.arange(2,5000,200) # 测试的范围
start_all = time.process_time()
for n in n_all:
print(n)
matrix_1 = np.zeros((n,n))
matrix_2 = np.zeros((n,n))
for i0 in range(n):
for j0 in range(n):
matrix_1[i0,j0] = np.random.uniform(-10, 10)
for i0 in range(n):
for j0 in range(n):
matrix_2[i0,j0] = np.random.uniform(-10, 10)
start = time.process_time()
matrix_3 = np.dot(matrix_1, matrix_2) # 矩阵乘积
end = time.process_time()
time_1 = np.append(time_1, [end-start], axis=0)
start = time.process_time()
matrix_4 = np.linalg.inv(matrix_1) # 矩阵求逆
end = time.process_time()
time_2 = np.append(time_2, [end-start], axis=0)
start = time.process_time()
eigenvalue, eigenvector = np.linalg.eig(matrix_1) # 求矩阵本征值
end = time.process_time()
time_3 = np.append(time_3, [end-start], axis=0)
end_all = time.process_time()
print('总共运行时间:', (end_all-start_all)/60, '分')
plt.subplot(131)
plt.xlabel('n^3/10^9')
plt.ylabel('时间(秒)')
plt.title('矩阵乘积')
plt.plot((n_all/10**3)*(n_all/10**3)*(n_all/10**3), time_1, 'o-')
plt.subplot(132)
plt.xlabel('n^3/10^9')
plt.title('矩阵求逆')
plt.plot((n_all/10**3)*(n_all/10**3)*(n_all/10**3), time_2, 'o-')
plt.subplot(133)
plt.xlabel('n^3/10^9')
plt.title('求矩阵本征值')
plt.plot((n_all/10**3)*(n_all/10**3)*(n_all/10**3), time_3, 'o-')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 在画图中正常显示中文
plt.rcParams['axes.unicode_minus'] = False # 中文化后,加上这个使正常显示负号
plt.show()
计算结果为(运算总时长约 40 分钟):
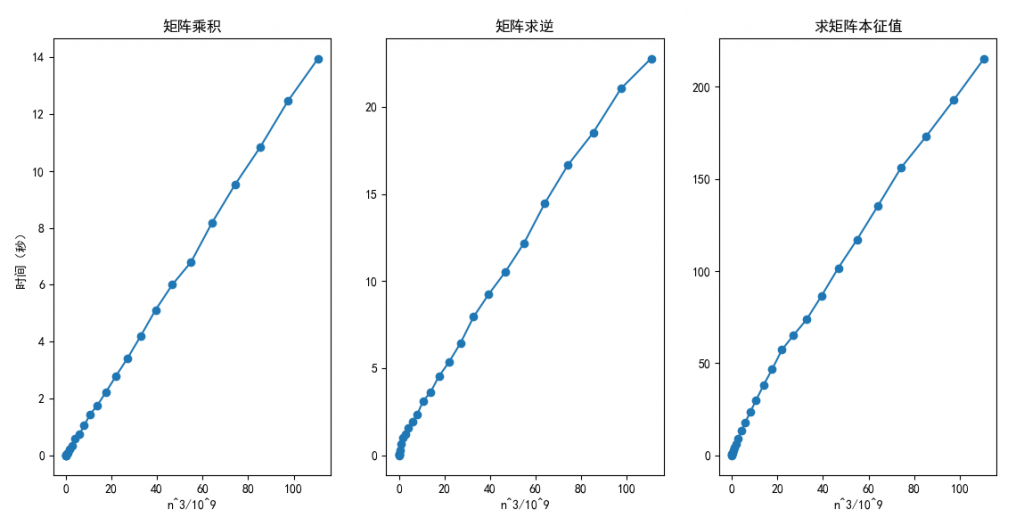
可以看出:矩阵乘积、矩阵求逆、求矩阵本征值的运算时间均与 ![]() 成正比。
成正比。
参考资料:
[1] https://topocondmat.org/w8_general/invariants.html
[2] https://zhidao.baidu.com/question/576048393.html
[3] http://muchong.com/html/201403/7080180.html
[4] https://zhidao.baidu.com/question/450632688.html
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】