矩阵的特征向量是有朝向的,通常写为列向量。这里给出特性向量在矩阵中朝向的验证。
先给出结论:
- Python中numpy.linalg.eig求解特征向量在矩阵中的朝向为列向量。
- Matlab中eig求解特征向量在矩阵中的朝向为列向量。
- Mathematica中Eigenvectors求解特征向量在矩阵中的朝向为横向量(只有这里为横向量)。
- Fortran中lapack的geev求解特征向量在矩阵中的朝向为列向量。
计算矩阵特征向量的例子[1]:



一、Python中的numpy.linalg.eig验证
numpy.linalg.eig 官方文档:https://numpy.org/doc/stable/reference/generated/numpy.linalg.eig.html
Python 代码验证:
import numpy as np
A = np.array([[3, 2, -1], [-2, -2, 2], [3, 6, -1]])
eigenvalue, eigenvector = np.linalg.eig(A)
print('矩阵:\n', A)
print('特征值:\n', eigenvalue)
print('特征向量:\n', eigenvector)
print('特征值为-4对应的特征向量理论值:\n', np.array([1/3, -2/3, 1])/np.sqrt((1/3)**2+(-2/3)**2+1**2))
print('\n判断是否正交:\n', np.dot(eigenvector.transpose(), eigenvector))
print('判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose()))
print('特征向量矩阵的列向量模方和:')
for i in range(3):
print(eigenvector[0, i]**2+eigenvector[1, i]**2+eigenvector[2, i]**2)
print('特征向量矩阵的行向量模方和:')
for i in range(3):
print(eigenvector[i, 0]**2+eigenvector[i, 1]**2+eigenvector[i, 2]**2)
运算结果:
矩阵:
[[ 3 2 -1]
[-2 -2 2]
[ 3 6 -1]]
特征值:
[ 2. -4. 2.]
特征向量:
[[ 0.88900089 0.26726124 0.2140049 ]
[-0.25400025 -0.53452248 0.34914907]
[ 0.38100038 0.80178373 0.91230304]]
特征值为-4对应的特征向量理论值:
[ 0.26726124 -0.53452248 0.80178373]
判断是否正交:
[[1. 0.67884423 0.4491544 ]
[0.67884423 1. 0.60203691]
[0.4491544 0.60203691 1. ]]
判断是否正交:
[[ 0.90754925 -0.29394398 0.74823271]
[-0.29394398 0.47213549 -0.20681587]
[ 0.74823271 -0.20681587 1.62031526]]
特征向量矩阵的列向量模方和:
0.9999999999999998
0.9999999999999999
1.0
特征向量矩阵的行向量模方和:
0.9075492482141987
0.4721354876041147
1.6203152641816863结论:Python 中 numpy.linalg.eig 求解特征向量在矩阵中的朝向为列向量。
二、Matlab中的eig验证
eig 官方文档:https://www.mathworks.com/help/matlab/ref/eig.html
Matlab 代码验证:
clc;clear all;
A = [3, 2, -1; -2, -2, 2; 3, 6, -1]
[V,D] = eig(A)运算结果:
A =
3 2 -1
-2 -2 2
3 6 -1
V =
0.8890 0.2673 -0.0100
-0.2540 -0.5345 0.4512
0.3810 0.8018 0.8924
D =
2.0000 0 0
0 -4.0000 0
0 0 2.0000结论:Matlab 中 eig 求解特征向量在矩阵中的朝向为列向量。
三、Mathematica中的Eigenvectors验证
Eigenvectors 官方文档:https://reference.wolfram.com/language/ref/Eigenvectors.html
MMA 代码验证:
Clear["`*"]
A = {{3, 2, -1}, {-2, -2, 2}, {3, 6, -1}};
MatrixForm[A]
eigenvalue = MatrixForm[Eigenvalues[A]]
eigenvector = MatrixForm[Eigenvectors[A]]运算结果:
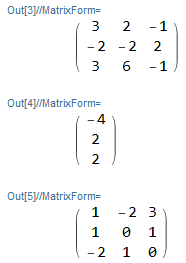
结论:Mathematica 中 Eigenvectors 求解特征向量在矩阵中的朝向为横向量。
四、Fortran中lapack的geev验证
用到 MKL-lapack 中的 geev 函数。
Fortran 代码验证:
program main
use lapack95
implicit none
integer i,j,info
complex*16 A(3,3), eigenvalues(3), eigenvectors(3,3)
A(1,1)=(3.d0, 0.d0)
A(1,2)=(2.d0, 0.d0)
A(1,3)=(-1.d0, 0.d0)
A(2,1)=(-2.d0, 0.d0)
A(2,2)=(-2.d0, 0.d0)
A(2,3)=(2.d0, 0.d0)
A(3,1)=(3.d0, 0.d0)
A(3,2)=(6.d0, 0.d0)
A(3,3)=(-1.d0, 0.d0)
write(*,*) 'matrix:'
do i=1,3
do j=1,3
write(*,"(f10.4, '+1i*',f7.4)",advance='no') A(i,j) ! 内循环为列的指标
enddo
write(*,*) ''
enddo
call geev(A=A, W=eigenvalues, VR=eigenvectors, INFO=info)
write(*,*) 'eigenvectors:'
do i=1,3
do j=1,3
write(*,"(f10.4, '+1i*',f7.4)",advance='no') eigenvectors(i,j) ! 内循环为列的指标。输出结果列向量为特征向量。
enddo
write(*,*) ''
enddo
write(*,*) 'eigenvalues:'
do i=1,3
write(*,"(f10.4, '+1i*',f7.4)",advance='no') eigenvalues(i)
enddo
write(*,*) ''
write(*,*) ''
end program运算结果:
matrix:
3.0000+1i* 0.0000 2.0000+1i* 0.0000 -1.0000+1i* 0.0000
-2.0000+1i* 0.0000 -2.0000+1i* 0.0000 2.0000+1i* 0.0000
3.0000+1i* 0.0000 6.0000+1i* 0.0000 -1.0000+1i* 0.0000
eigenvectors:
0.8890+1i* 0.0000 0.2673+1i* 0.0000 0.1654+1i* 0.0000
-0.2540+1i* 0.0000 -0.5345+1i* 0.0000 0.3737+1i* 0.0000
0.3810+1i* 0.0000 0.8018+1i* 0.0000 0.9127+1i* 0.0000
eigenvalues:
2.0000+1i* 0.0000 -4.0000+1i* 0.0000 2.0000+1i* 0.0000结论:Fortran 中 lapack 的 geev 求解特征向量在矩阵中的朝向为列向量。
五、实对称矩阵的验证(使用Python)
Python 代码验证:
import numpy as np
A = np.array([[3, 2, -1], [2, -2, 6], [-1, 6, 1]])
eigenvalue, eigenvector = np.linalg.eig(A)
print('矩阵:\n', A)
print('特征值:\n', eigenvalue)
print('特征向量:\n', eigenvector)
print('\n判断是否正交:\n', np.dot(eigenvector.transpose(), eigenvector))
print('判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose()))
print('特征向量矩阵的列向量模方和:')
for i in range(3):
print(eigenvector[0, i]**2+eigenvector[1, i]**2+eigenvector[2, i]**2)
print('特征向量矩阵的行向量模方和:')
for i in range(3):
print(eigenvector[i, 0]**2+eigenvector[i, 1]**2+eigenvector[i, 2]**2)
print('\n对角化验证:')
print(np.dot(np.dot(eigenvector.transpose(), A), eigenvector))
print(np.dot(np.dot(eigenvector, A), eigenvector.transpose()))
运算结果:
矩阵:
[[ 3 2 -1]
[ 2 -2 6]
[-1 6 1]]
特征值:
[-7.15829251 3.39135682 5.76693569]
特征向量:
[[-0.21121062 0.96022113 0.18266214]
[ 0.77488229 0.0505841 0.63007832]
[-0.59577471 -0.27462089 0.75474225]]
判断是否正交:
[[ 1.00000000e+00 1.33991245e-16 -1.63400129e-16]
[ 1.33991245e-16 1.00000000e+00 -2.02152020e-16]
[-1.63400129e-16 -2.02152020e-16 1.00000000e+00]]
判断是否正交:
[[ 1.00000000e+00 3.01473427e-17 -1.98942238e-16]
[ 3.01473427e-17 1.00000000e+00 2.51221888e-17]
[-1.98942238e-16 2.51221888e-17 1.00000000e+00]]
特征向量矩阵的列向量模方和:
1.0
1.0000000000000002
1.0000000000000002
特征向量矩阵的行向量模方和:
1.0000000000000002
1.0
1.0000000000000004
对角化验证:
[[-7.15829251e+00 -3.56211600e-16 9.06925743e-16]
[-1.83305982e-16 3.39135682e+00 -1.01923929e-15]
[ 3.55008849e-16 -8.84047462e-16 5.76693569e+00]]
[[-0.30617673 4.67076984 4.33018775]
[ 4.67076984 1.75598604 -2.38608731]
[ 4.33018775 -2.38608731 0.55019069]]结论1:虽然实对称矩阵的特征向量组成的矩阵为正交矩阵,即列向量和横向量均是标准正交组,但从最后“对角化验证”中可以看出:特征向量只能是列向量。
这里再给出一个实对称矩阵的例子:
import numpy as np
A = np.array([[0, 1, 1, -1], [1, 0, -1, 1], [1, -1, 0, 1], [-1, 1, 1, 0]])
eigenvalue, eigenvector = np.linalg.eig(A)
print('矩阵:\n', A)
print('特征值:\n', eigenvalue)
print('特征向量:\n', eigenvector)
print('\n判断是否正交:\n', np.dot(eigenvector.transpose(), eigenvector))
print('判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose()))
print('特征向量矩阵的列向量模方和:')
for i in range(4):
print(eigenvector[0, i]**2+eigenvector[1, i]**2+eigenvector[2, i]**2+eigenvector[3, i]**2)
print('特征向量矩阵的行向量模方和:')
for i in range(4):
print(eigenvector[i, 0]**2+eigenvector[i, 1]**2+eigenvector[i, 2]**2+eigenvector[i, 3]**2)
print('\n对角化验证:')
print(np.dot(np.dot(eigenvector.transpose(), A), eigenvector))
print(np.dot(np.dot(eigenvector, A), eigenvector.transpose()))
print('\n特征向量理论值:')
T = np.array([[1/np.sqrt(2), 1/np.sqrt(6), -1/np.sqrt(12), 1/2], [1/np.sqrt(2), -1/np.sqrt(6), 1/np.sqrt(12), -1/2], [0, 2/np.sqrt(6), 1/np.sqrt(12), -1/2], [0, 0, 3/np.sqrt(12), 1/2]])
print(T)
print('\n判断是否正交:\n', np.dot(T.transpose(), T))
print('判断是否正交:\n', np.dot(T, T.transpose()))
print('\n对角化验证:')
print(np.dot(np.dot(T.transpose(), A), T))
print(np.dot(np.dot(T, A), T.transpose()))运算结果:
矩阵:
[[ 0 1 1 -1]
[ 1 0 -1 1]
[ 1 -1 0 1]
[-1 1 1 0]]
特征值:
[ 1. -3. 1. 1.]
特征向量:
[[ 0.8660254 0.5 0.12803516 0.08530895]
[ 0.28867513 -0.5 0.85020245 -0.16863006]
[ 0.28867513 -0.5 -0.36108364 0.80962746]
[-0.28867513 0.5 0.36108364 0.55568845]]
判断是否正交:
[[ 1.00000000e+00 5.55111512e-17 1.47842273e-01 9.85062898e-02]
[ 5.55111512e-17 1.00000000e+00 5.55111512e-17 -5.55111512e-17]
[ 1.47842273e-01 5.55111512e-17 1.00000000e+00 -2.24140369e-01]
[ 9.85062898e-02 -5.55111512e-17 -2.24140369e-01 1.00000000e+00]]
判断是否正交:
[[ 1.02367062 0.09447016 0.02283706 0.0936366 ]
[ 0.09447016 1.08461363 -0.11018839 -0.12004491]
[ 0.02283706 -0.11018839 1.11921136 -0.0138141 ]
[ 0.0936366 -0.12004491 -0.0138141 0.77250439]]
特征向量矩阵的列向量模方和:
0.9999999999999994
1.0
0.9999999999999998
0.9999999999999998
特征向量矩阵的行向量模方和:
1.0236706200685102
1.0846136343405914
1.1192113593415378
0.7725043862493592
对角化验证:
[[ 1.00000000e+00 -1.66533454e-16 1.47842273e-01 9.85062898e-02]
[-2.22044605e-16 -3.00000000e+00 -2.22044605e-16 0.00000000e+00]
[ 1.47842273e-01 -1.66533454e-16 1.00000000e+00 -2.24140369e-01]
[ 9.85062898e-02 1.11022302e-16 -2.24140369e-01 1.00000000e+00]]
[[ 0.91914825 0.16887985 -0.61063092 0.28569906]
[ 0.16887985 1.03164122 0.3407788 -0.25677458]
[-0.61063092 0.3407788 -2.71998308 1.15019912]
[ 0.28569906 -0.25677458 1.15019912 0.41958484]]
特征向量理论值:
[[ 0.70710678 0.40824829 -0.28867513 0.5 ]
[ 0.70710678 -0.40824829 0.28867513 -0.5 ]
[ 0. 0.81649658 0.28867513 -0.5 ]
[ 0. 0. 0.8660254 0.5 ]]
判断是否正交:
[[ 1.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 1.00000000e+00 1.38777878e-17 0.00000000e+00]
[ 0.00000000e+00 1.38777878e-17 1.00000000e+00 -5.55111512e-17]
[ 0.00000000e+00 0.00000000e+00 -5.55111512e-17 1.00000000e+00]]
判断是否正交:
[[ 1.00000000e+00 -2.22044605e-16 6.93889390e-17 -5.55111512e-17]
[-2.22044605e-16 1.00000000e+00 -6.93889390e-17 5.55111512e-17]
[ 6.93889390e-17 -6.93889390e-17 1.00000000e+00 5.55111512e-17]
[-5.55111512e-17 5.55111512e-17 5.55111512e-17 1.00000000e+00]]
对角化验证:
[[ 1.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 1.00000000e+00 1.38777878e-17 0.00000000e+00]
[ 5.55111512e-17 -2.77555756e-17 1.00000000e+00 1.66533454e-16]
[ 0.00000000e+00 1.11022302e-16 2.22044605e-16 -3.00000000e+00]]
[[-0.18272939 -0.35527542 1.74567822 0.39806493]
[-0.35527542 0.89328022 0.52437739 0.11957316]
[ 1.74567822 0.52437739 -1.57657624 -0.58753363]
[ 0.39806493 0.11957316 -0.58753363 0.8660254 ]]结论2:由于有相同的特征值,因此数值计算得到的特征向量矩阵不一定是正交矩阵,但可通过施密特正交化得到正交矩阵。参考博文:幺正矩阵和厄密矩阵、施密特正交化(附Python代码)。
六、厄密矩阵的验证(使用Python)
Python 代码验证:
import numpy as np
A = np.array([[3, 2+1j, -1], [2-1j, -2, 6], [-1, 6, 1]])
eigenvalue, eigenvector = np.linalg.eig(A)
print('矩阵:\n', A)
print('特征值:\n', eigenvalue)
print('特征向量:\n', eigenvector)
print('\n判断是否正交:\n', np.dot(eigenvector.transpose().conj(), eigenvector))
print('判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose().conj()))
print('特征向量矩阵的列向量模方和:')
for i in range(3):
print(np.abs(eigenvector[0, i])**2+np.abs(eigenvector[1, i])**2+np.abs(eigenvector[2, i])**2)
print('特征向量矩阵的行向量模方和:')
for i in range(3):
print(np.abs(eigenvector[i, 0])**2+np.abs(eigenvector[i, 1])**2+np.abs(eigenvector[i, 2])**2)
print('\n对角化验证:')
print(np.dot(np.dot(eigenvector.transpose().conj(), A), eigenvector))
print(np.dot(np.dot(eigenvector, A), eigenvector.transpose().conj()))运算结果:
矩阵:
[[ 3.+0.j 2.+1.j -1.+0.j]
[ 2.-1.j -2.+0.j 6.+0.j]
[-1.+0.j 6.+0.j 1.+0.j]]
特征值:
[-7.21794635-2.61492109e-16j 3.3020717 -2.54225846e-17j
5.91587465-1.57174516e-16j]
特征向量:
[[-0.20954515-0.07675339j 0.93023217+0.j 0.16392587+0.24082395j]
[ 0.77492229+0.j 0.05457078+0.0899991j 0.6219378 +0.04013732j]
[-0.59127654-0.00933973j -0.26185436+0.23456897j 0.725751 +0.j ]]
判断是否正交:
[[ 1.00000000e+00+0.00000000e+00j 5.58580959e-16-4.16333634e-17j
1.31838984e-16-8.32667268e-17j]
[ 5.58580959e-16+4.16333634e-17j 1.00000000e+00+0.00000000e+00j
-3.14852311e-16-3.88578059e-16j]
[ 1.31838984e-16+8.32667268e-17j -3.14852311e-16+3.88578059e-16j
1.00000000e+00+0.00000000e+00j]]
判断是否正交:
[[ 1.00000000e+00-1.58799564e-19j 1.80411242e-16-5.55111512e-17j
-3.60822483e-16-1.11022302e-16j]
[ 1.80411242e-16+5.55111512e-17j 1.00000000e+00+5.75391731e-19j
1.66533454e-16-2.28983499e-16j]
[-3.60822483e-16+1.11022302e-16j 1.66533454e-16+2.22044605e-16j
1.00000000e+00+1.99986029e-18j]]
特征向量矩阵的列向量模方和:
1.0
0.9999999999999999
1.0000000000000004
特征向量矩阵的行向量模方和:
0.9999999999999994
1.0000000000000004
1.0000000000000004
对角化验证:
[[-7.21794635e+00-2.77555756e-17j -1.06165077e-15-2.77555756e-16j
-2.77555756e-17+2.33146835e-15j]
[-1.00180281e-15+4.44089210e-16j 3.30207170e+00-2.77555756e-17j
-1.54563862e-15-1.66533454e-15j]
[-4.02455846e-16-2.31759056e-15j -1.34614542e-15+1.55431223e-15j
5.91587465e+00+5.55111512e-17j]]
[[-0.19776356+2.22044605e-16j 4.57467765-9.58639473e-01j
4.27645354+1.07172067e+00j]
[ 4.57467765+9.58639473e-01j 1.96312924-5.55111512e-17j
-2.15714313-1.04374721e+00j]
[ 4.27645354-1.07172067e+00j -2.15714313+1.04374721e+00j
0.23463432+2.22044605e-16j]]参考资料:
[1] 截图自北京科技大学廖福成老师的”高等代数与解析几何“课件
[2] ”高等代数与解析几何“、”线性代数“、”高等数学“等相关教材
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】