能带和谱函数(spectral function)在实验上可以通过角分辨光电子能谱 ARPES (angle resolved photoemission spectroscopy)中得到。准粒子干涉图案 QPI (quasiparticle interference) 在实验上可以由扫描隧道显微镜 STM(scanning tunneling microscope)中观察到,也称为扫描隧道谱FT-FTS (Fourier transform scanning tunneling spectroscopy)。
QPI 的物理意义是杂质引起的局域态密度转移在倒空间的图像,英文为:the Fourier transform of the induced local density of states。QPI 的公式主要参考这篇文献:Quasiparticle scattering interference in superconducting iron pnictides。
一、Fortran代码
这里代码中的哈密顿量和参数均是参考上面这篇文献。以重复文献中图 4(e) 的结果为例,代码如下(按照当前步长的精度,在个人计算机上运算大概需要 4 个小时):
! This code is supported by the website: https://www.guanjihuan.com
! The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3785
module global
implicit none
double precision sqrt3,Pi
parameter(sqrt3=1.7320508075688773d0,Pi=3.14159265358979324d0)
end module global
program QPI !QPI主程序
use blas95
use lapack95,only:GETRF,GETRI
use global
implicit none
integer i,j,info,index_0(4)
double precision omega,kx,ky,Eigenvalues(4),eta,V0,kx1,kx2,ky1,ky2,qx,qy,time_begin,time_end
parameter(eta=0.005)
complex*16 H0(4,4),green_0(4,4),green_1(4,4),green_0_k1(4,4),green_0_k2(4,4),A_spectral,V(4,4),gamma_0(4,4),Temp_0(4,4),T(4,4),g_1,rho_1
character(len=*):: Flname
parameter(Flname='') !可以写上输出文件路径,也可以不写,输出存在当前文件的路径
omega=0.070d0
open(unit=10,file=Flname//'Spectral function_w=0.07.txt')
open(unit=20,file=Flname//'QPI_intra_nonmag_w=0.07.txt')
call CPU_TIME(time_begin)
!计算谱函数A(kx,ky)
write(10,"(f20.10,x)",advance='no') 0
do ky=-Pi,Pi,0.01d0 !谱函数图案的精度
write(10,"(f20.10,x)",advance='no') ky
enddo
write(10,"(a)",advance='yes') ' '
do kx=-Pi,Pi,0.01d0 !谱函数图案的精度
write(10,"(f20.10,x)",advance='no') kx
do ky=-Pi,Pi,0.01d0 !谱函数图案的精度
call Greenfunction_clean(kx,ky,eta,omega,green_0)
A_spectral=-(green_0(1,1)+green_0(3,3))/Pi
write(10,"(f20.10)",advance='no') imag(A_spectral)
enddo
write(10,"(a)",advance='yes') ' '
enddo
!计算QPI(qx,qy)
V0=0.4d0
V=0.d0
V(1,1)=V0
V(2,2)=-V0
V(3,3)=V0
V(4,4)=-V0
gamma_0=0.d0
do kx=-Pi,Pi,0.01
do ky=-Pi,Pi,0.01
call Greenfunction_clean(kx,ky,eta,omega,green_0)
do i=1,4
do j=1,4
gamma_0(i,j)=gamma_0(i,j)+green_0(i,j)*0.01*0.01
enddo
enddo
enddo
enddo
gamma_0=gamma_0/(2*Pi)/(2*Pi)
call gemm(V,gamma_0,Temp_0)
do i=1,4
Temp_0(i,i)=1-Temp_0(i,i)
enddo
call GETRF( Temp_0,index_0,info ); call GETRI( Temp_0,index_0,info) !求逆
call gemm(Temp_0,V,T) !矩阵乘积
write(20,"(f20.10,x)",advance='no') 0
do qy=-Pi,Pi,0.01 !QPI图案的精度
write(20,"(f20.10,x)",advance='no') qy
enddo
write(20,"(a)",advance='yes') ' '
do qx=-Pi,Pi,0.01 !QPI图案的精度
write(*,"(a)",advance='no') 'qx='
write(*,*) qx !屏幕输出可以实时查看计算进度
write(20,"(f20.10)",advance='no') qx
do qy=-Pi,Pi,0.01 !QPI图案的精度
rho_1=0.d0
do kx1=-Pi,Pi,0.06 !积分的精度
kx2=kx1+qx
do ky1=-Pi,Pi,0.06 !积分的精度
ky2=ky1+qy
call Greenfunction_clean(kx1,ky1,eta,omega,green_0_k1)
call Greenfunction_clean(kx2,ky2,eta,omega,green_0_k2)
call gemm(green_0_k1,T,Temp_0)
call gemm(Temp_0, green_0_k2, green_1)
g_1=green_1(1,1)-dconjg(green_1(1,1))+green_1(3,3)-dconjg(green_1(3,3))
rho_1=rho_1+g_1*0.06*0.06
enddo
enddo
rho_1=rho_1/(2*Pi)/(2*Pi)/(2*Pi)*(0.d0,1.d0)
write(20,"(f20.10,x,f20.10)",advance='no') real(rho_1)
enddo
write(20,"(a)",advance='yes') ' '
enddo
call CPU_TIME(time_end)
write(*,"(a)",advance='no') 'The running time of this task='
write (*,*) time_end-time_begin !屏幕输出总的计算时间,单位为秒(按照当前步长的精度,在个人计算机上运算大概需要4个小时)
end program
subroutine Greenfunction_clean(kx,ky,eta,omega,green_0) !干净体系的格林函数
use blas95
use lapack95,only:GETRF,GETRI
use global
integer info,index_0(4)
double precision, intent(in):: kx,ky,eta,omega
complex*16 H0(4,4)
complex*16,intent(out):: green_0(4,4)
call Hamiltonian(kx,ky,H0)
green_0=H0
do i=1,4
green_0(i,i)=omega+(0.d0,1.d0)*eta-green_0(i,i)
enddo
call GETRF( green_0,index_0,info ); call GETRI( green_0,index_0,info );
end subroutine Greenfunction_clean
subroutine Hamiltonian(kx,ky,Matrix) !哈密顿量
use global
implicit none
integer i,j
double precision t1,t2,t3,t4,mu,epsilon_x,epsilon_y,epsilon_xy,delta_1,delta_2,delta_0
double precision, intent(in):: kx,ky
complex*16,intent(out):: Matrix(4,4)
t1=-1;t2=1.3;t3=-0.85;t4=-0.85;delta_0=0.1;mu=1.54
Matrix=(0.d0,0.d0)
epsilon_x=-2*t1*dcos(kx)-2*t2*dcos(ky)-4*t3*dcos(kx)*dcos(ky)
epsilon_y=-2*t1*dcos(ky)-2*t2*dcos(kx)-4*t3*dcos(kx)*dcos(ky)
epsilon_xy=-4*t4*dsin(kx)*dsin(ky)
delta_1=delta_0*dcos(kx)*dcos(ky)
delta_2=delta_1
Matrix(1,1)=epsilon_x-mu
Matrix(2,2)=-epsilon_x+mu
Matrix(3,3)=epsilon_y-mu
Matrix(4,4)=-epsilon_y+mu
Matrix(1,2)=delta_1
Matrix(2,1)=delta_1
Matrix(1,3)=epsilon_xy
Matrix(3,1)=epsilon_xy
Matrix(1,4)=0.d0
Matrix(4,1)=0.d0
Matrix(2,3)=0.d0
Matrix(3,2)=0.d0
Matrix(2,4)=-epsilon_xy
Matrix(4,2)=-epsilon_xy
Matrix(3,4)=delta_2
Matrix(4,3)=delta_2
end subroutine Hamiltonian计算的谱函数图像为:
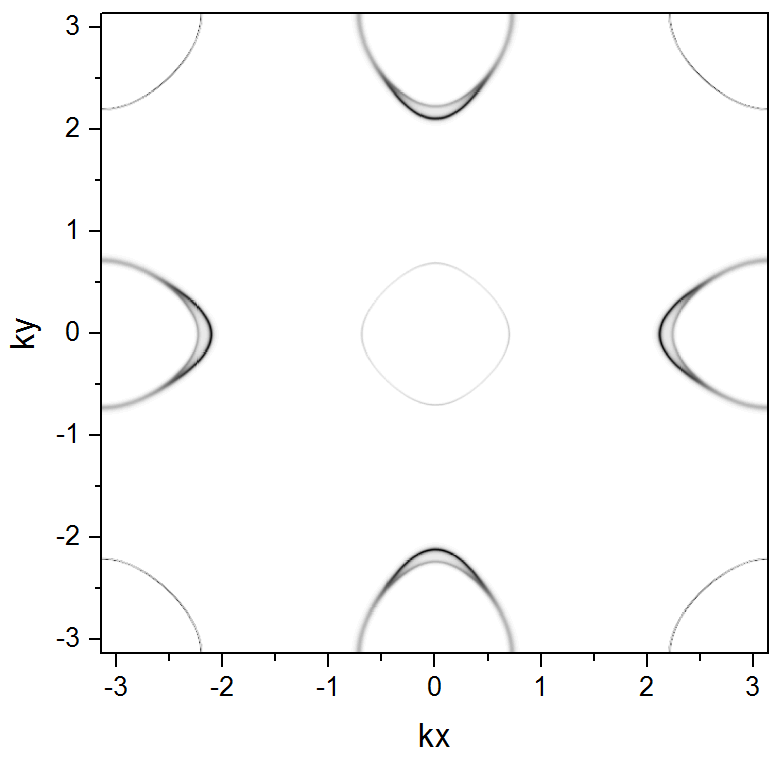
计算的 QPI 图像为(由于“计算精度”的选取以及“颜色值范围”选取的原因,这里结果和文献中还略有些不同,但基本上是重复了出结果):
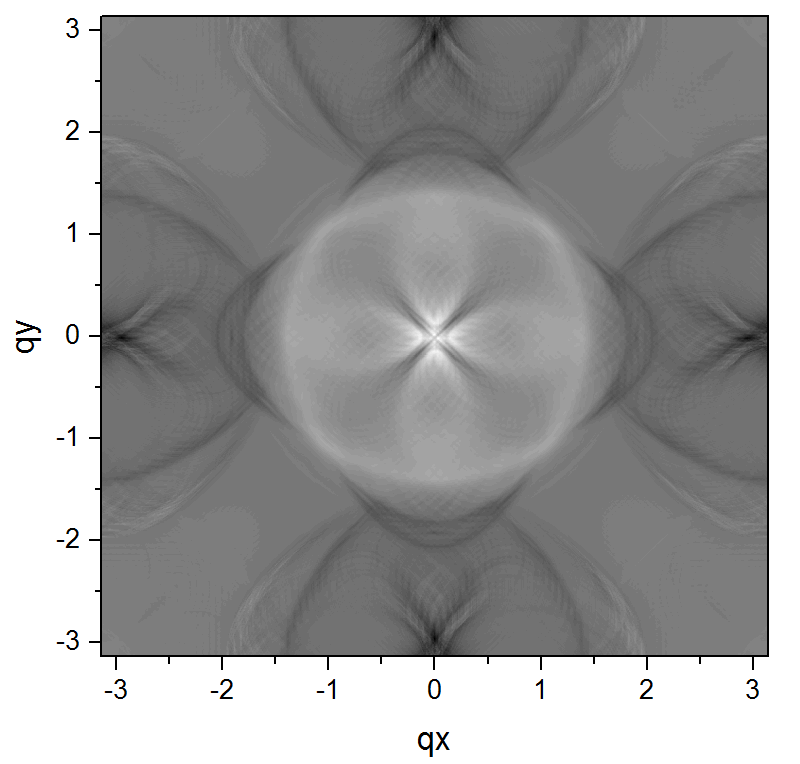
二、Python代码
Python 代码如下(按当前计算参数和精度,计算时间约为三四天, 83 个小时。这里不建议使用 Python,推荐使用 Fortran 代码,因为这里循环很多,Python 耗时是 Fortran 的十几倍):
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3785
"""
import numpy as np
from math import *
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import time
def green_function(fermi_energy, k1, k2, hamiltonian): # 计算格林函数
matrix0 = hamiltonian(k1, k2)
dim = matrix0.shape[0]
green = np.linalg.inv(fermi_energy * np.identity(dim) - matrix0)
return green
def spectral_function(fermi_energy, k1, k2, hamiltonian): # 计算谱函数
dim1 = k1.shape[0]
dim2 = k2.shape[0]
spectrum = np.zeros((dim1, dim2))
i0 = 0
for k10 in k1:
j0 = 0
for k20 in k2:
green = green_function(fermi_energy, k10, k20, hamiltonian)
spectrum[i0, j0] = (np.imag(green[0,0])+np.imag(green[2,2]))/(-pi)
j0 += 1
i0 += 1
# print(spectrum)
print()
print('Spectral function显示的网格点 =', k1.shape[0], '*', k1.shape[0], '; 步长 =', k1[1] - k1[0])
print()
return spectrum
def qpi(fermi_energy, q1, q2, hamiltonian, potential_i): # 计算QPI
dim = hamiltonian(0, 0).shape[0]
ki1 = np.arange(-pi, pi, 0.01) # 计算gamma_0时,k的积分密度
ki2 = np.arange(-pi, pi, 0.01)
print('gamma_0的积分网格点 =', ki1.shape[0], '*', ki1.shape[0], '; 步长 =', ki1[1] - ki1[0])
gamma_0 = integral_of_green(fermi_energy, ki1, ki2, hamiltonian)/np.square(2*pi)
t_matrix = np.dot(np.linalg.inv(np.identity(dim)-np.dot(potential_i, gamma_0)), potential_i)
ki1 = np.arange(-pi, pi, 0.06) # 计算induced_local_density时,k的积分密度
ki2 = np.arange(-pi, pi, 0.06)
print('局域态密度变化的积分网格点 =', ki1.shape[0], '*', ki1.shape[0], '; 步长 =', ki1[1] - ki1[0])
print('QPI显示的网格点 =', q1.shape[0], '*', q1.shape[0], '; 步长 =', q1[1] - q1[0])
step_length = ki1[1] - ki1[0]
induced_local_density = np.zeros((q1.shape[0], q2.shape[0]))*(1+0j)
print()
i0 = 0
for q10 in q1:
print('i0=', i0)
j0 = 0
for q20 in q2:
for ki10 in ki1:
for ki20 in ki2:
green_01 = green_function(fermi_energy, ki10, ki20, hamiltonian)
green_02 = green_function(fermi_energy, ki10+q10, ki20+q20, hamiltonian)
induced_green = np.dot(np.dot(green_01, t_matrix), green_02)
temp = induced_green[0, 0]-induced_green[0, 0].conj()+induced_green[2, 2]-induced_green[2, 2].conj()
induced_local_density[i0, j0] = induced_local_density[i0, j0]+temp*np.square(step_length)
j0 += 1
i0 += 1
write_matrix_k1_k2(q1, q2, np.real(induced_local_density*1j/np.square(2*pi)/(2*pi)), 'QPI') # 数据写入文件(临时写入,会被多次替代)
induced_local_density = np.real(induced_local_density*1j/np.square(2*pi)/(2*pi))
return induced_local_density
def integral_of_green(fermi_energy, ki1, ki2, hamiltonian): # 在计算QPI时需要对格林函数积分
dim = hamiltonian(0, 0).shape[0]
integral_value = np.zeros((dim, dim))*(1+0j)
step_length = ki1[1]-ki1[0]
for ki10 in ki1:
for ki20 in ki2:
green = green_function(fermi_energy, ki10, ki20, hamiltonian)
integral_value = integral_value+green*np.square(step_length)
return integral_value
def write_matrix_k1_k2(x1, x2, value, filename='matrix_k1_k2'): # 把矩阵数据写入文件(格式化输出)
with open(filename+'.txt', 'w') as f:
np.set_printoptions(suppress=True) # 取消输出科学记数法
f.write('0 ')
for x10 in x1:
f.write(str(x10)+' ')
f.write('\n')
i0 = 0
for x20 in x2:
f.write(str(x20))
for j0 in range(x1.shape[0]):
f.write(' '+str(value[i0, j0])+' ')
f.write('\n')
i0 += 1
def plot_contour(x1, x2, value, filename='contour'): # 直接画出contour图像(保存图像)
plt.contourf(x1, x2, value) #, cmap=plt.cm.hot)
plt.savefig(filename+'.eps')
# plt.show()
def hamiltonian(kx, ky): # 体系的哈密顿量
t1 = -1; t2 = 1.3; t3 = -0.85; t4 = -0.85; delta_0 = 0.1; mu = 1.54
epsilon_x = -2*t1*cos(kx)-2*t2*cos(ky)-4*t3*cos(kx)*cos(ky)
epsilon_y = -2*t1*cos(ky)-2*t2*cos(kx)-4*t3*cos(kx)*cos(ky)
epsilon_xy = -4*t4*sin(kx)*sin(ky)
delta_1 = delta_0*cos(kx)*cos(ky)
delta_2 = delta_0*cos(kx)*cos(ky)
h = np.zeros((4, 4))
h[0, 0] = epsilon_x-mu
h[1, 1] = -epsilon_x+mu
h[2, 2] = epsilon_y-mu
h[3, 3] = -epsilon_y+mu
h[0, 1] = delta_1
h[1, 0] = delta_1
h[0, 2] = epsilon_xy
h[2, 0] = epsilon_xy
h[0, 3] = 0
h[3, 0] = 0
h[1, 2] = 0
h[2, 1] = 0
h[1, 3] = -epsilon_xy
h[3, 1] = -epsilon_xy
h[2, 3] = delta_2
h[3, 2] = delta_2
return h
def main(): # 主程序
start_clock = time.perf_counter()
fermi_energy = 0.07 # 费米能
energy_broadening_width = 0.005 # 展宽
k1 = np.arange(-pi, pi, 0.01) # 谱函数的图像精度
k2 = np.arange(-pi, pi, 0.01)
spectrum = spectral_function(fermi_energy+energy_broadening_width*1j, k1, k2, hamiltonian) # 调用谱函数子程序
write_matrix_k1_k2(k1, k2, spectrum, 'Spectral_function') # 把谱函数的数据写入文件
# plot_contour(k1, k2, spectrum, 'Spectral_function') # 直接显示谱函数的图像(保存图像)
q1 = np.arange(-pi, pi, 0.01) # QPI数的图像精度
q2 = np.arange(-pi, pi, 0.01)
potential_i = (0.4+0j)*np.identity(hamiltonian(0, 0).shape[0]) # 杂质势
potential_i[1, 1] = - potential_i[1, 1] # for nonmagnetic
potential_i[3, 3] = - potential_i[3, 3]
induced_local_density = qpi(fermi_energy+energy_broadening_width*1j, q1, q2, hamiltonian, potential_i) # 调用QPI子程序
write_matrix_k1_k2(q1, q2, induced_local_density, 'QPI') # 把QPI数据写入文件(这里用的方法是计算结束后一次性把数据写入)
# plot_contour(q1, q2, induced_local_density, 'QPI') # 直接显示QPI图像(保存图像)
end_clock = time.perf_counter()
print('CPU执行时间=', end_clock - start_clock)
if __name__ == '__main__':
main()
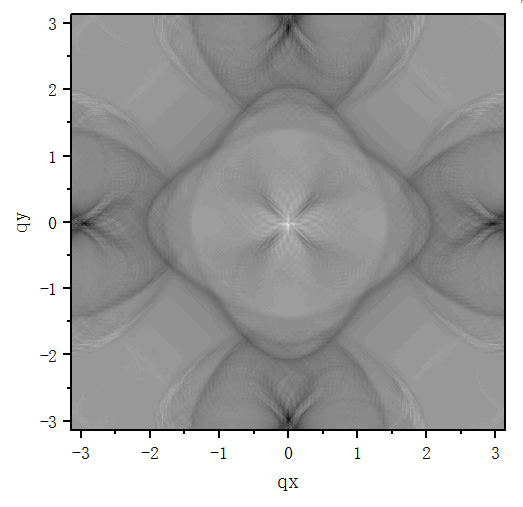
用 Python 和 Fortran 计算,谱函数的数值结果完全相同,而 QPI 的数值结果在细节上还是会些区别(暂时找不到原因,有可能是数值精度导致的正常现象),但画出的图案是相似的,QPI 图案为:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】