外尔半金属的哈密顿量和费米弧（附Python代码）

1. 外尔半金属能带

外尔半金属最小模型[1,2,3]：

$H=A(k_x \sigma_{x}+k_y \sigma_{y})+M_{k}\sigma_{z}$

其中， $M_k=M_0-M_1(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})$

本征值为：

$E_{\pm}=\pm \sqrt{M_{k}^{2}+A^{2}(k_{x}^{2}+k_{y}^{2})}$

两个外尔点的坐标为 $(0, 0,\pm k_c)$ ，其中 $k_c \equiv \sqrt{M_0/M_1}$

计算能带的Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6077
"""

import numpy as np
from math import *
import matplotlib.pyplot as plt


def main():
    n =  0.5
    k1 = np.arange(-n*pi, n*pi, n/20)
    k2 = np.arange(-n*pi, n*pi, n/20)
    plot_bands_two_dimension(k1, k2, hamiltonian)


def hamiltonian(kx,kz,ky=0):  # Weyl semimetal
    A = 1
    M0 = 1
    M1 = 1
    H = A*(kx*sigma_x()+ky*sigma_y())+(M0-M1*(kx**2+ky**2+kz**2))*sigma_z()
    return H


def sigma_x():
    return np.array([[0, 1],[1, 0]])


def sigma_y():
    return np.array([[0, -1j],[1j, 0]])


def sigma_z():
    return np.array([[1, 0],[0, -1]])


def plot_bands_two_dimension(k1, k2, hamiltonian):
    from mpl_toolkits.mplot3d import Axes3D
    from matplotlib import cm
    from matplotlib.ticker import LinearLocator, FormatStrFormatter
    dim = hamiltonian(0, 0).shape[0]
    dim1 = k1.shape[0]
    dim2 = k2.shape[0]
    eigenvalue_k = np.zeros((dim2, dim1, dim))
    i0 = 0
    for k10 in k1:
        j0 = 0
        for k20 in k2:
            matrix0 = hamiltonian(k10, k20)
            eigenvalue, eigenvector = np.linalg.eig(matrix0)
            eigenvalue_k[j0, i0, :] = np.sort(np.real(eigenvalue[:]))
            j0 += 1
        i0 += 1
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    k1, k2 = np.meshgrid(k1, k2)
    for dim0 in range(dim):
        ax.plot_surface(k1, k2, eigenvalue_k[:, :, dim0], cmap=cm.coolwarm, linewidth=0, antialiased=False)
    plt.xlabel('kx')
    plt.ylabel('kz') 
    ax.set_zlabel('E')  
    plt.show()


if __name__ == '__main__':
    main()

计算结果为：

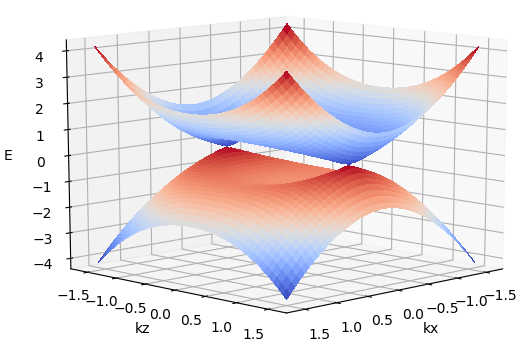
2. 外尔半金属的费米弧

通过推导[2]（这里推导过程略），可得到y=0表面态的哈密顿量：

$E_{\mathrm{arc}}(k_x, k_z)= sgn(M)Ak_x$

在推导过程中，表面态还有以下限制：

$k_{x}^{2}+k_{z}^{2}<k_{c}^{2}$

在这里给定一个费米能，表面态（费米弧）是一条线段。当费米能 $E=0$ 时， $k_x=0$ ，该线段为 $|k_z|<|k_c|$ ，连接两个外尔点。

计算表面态的Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6077
"""

import numpy as np
from math import *
import matplotlib.pyplot as plt


def main():
    n =  0.5
    k1 = np.arange(-n*pi, n*pi, n/50)
    k2 = np.arange(-n*pi, n*pi, n/50)
    plot_bands_two_dimension_direct(k1, k2, hamiltonian)


def hamiltonian(kx,kz,ky=0):  # surface states of Weyl semimetal
    A = 1
    H = A*kx
    return H


def sigma_x():
    return np.array([[0, 1],[1, 0]])


def sigma_y():
    return np.array([[0, -1j],[1j, 0]])


def sigma_z():
    return np.array([[1, 0],[0, -1]])


def plot_bands_two_dimension_direct(k1, k2, hamiltonian):
    from mpl_toolkits.mplot3d import Axes3D
    from matplotlib import cm
    from matplotlib.ticker import LinearLocator, FormatStrFormatter
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    dim1 = k1.shape[0]
    dim2 = k2.shape[0]
    eigenvalue_k = np.zeros((dim2, dim1))
    i0 = 0   
    for k10 in k1:
        j0 = 0
        for k20 in k2:
            if (k10**2+k20**2 <= 1):
                eigenvalue_k[j0, i0] = hamiltonian(k10, k20)
            else:
                eigenvalue_k[j0, i0] = 'nan'
            j0 += 1
        i0 += 1
    k1, k2 = np.meshgrid(k1, k2)
    ax.scatter(k1, k2, eigenvalue_k)
    plt.xlabel('kx')
    plt.ylabel('kz')
    ax.set_zlabel('E')  
    plt.show()


if __name__ == '__main__':
    main()

计算结果为：

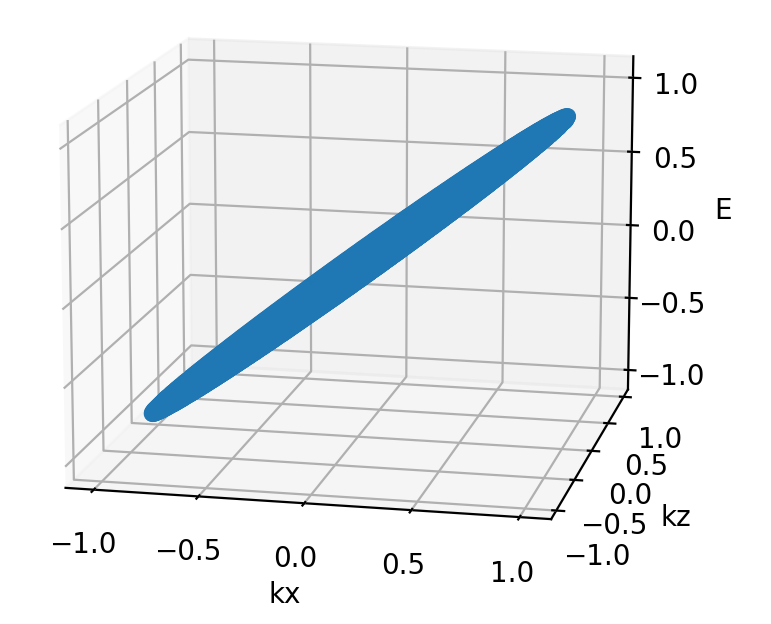
3. 外尔半金属哈密顿量的另外一个形式

外尔半金属最小模型在文献中常见的形式还有[4]：

$H=A(k_x\sigma_{x}+k_y\sigma_{y})+M(k_{w}^{2}-k^{2})\sigma_{z}$

该形式与上面那种形式是等价的。对应关系为：

$M_0 \to Mk_{w}^{2}$

$M_1 \to M$

这里外尔点的坐标为： $(0, 0, \pm k_w)$

加入平庸项后哈密顿量写为：

$H=D_{1}k_{y}^{2}+D_{2}(k_{x}^{2}+k_{z}^{2})+A(k_x\sigma_{x}+k_y\sigma_{y})+M(k_{w}^{2}-k^{2})\sigma_{z}$

通过推导，可得到y=0表面态的哈密顿量：

$H_{\mathrm{arc}}=D_1 k_{w}^{2}+vk_x+(D_2-D_1)(k_{x}^{2}+k_{z}^{2})$

其中， $v \equiv A\sqrt{M^2-D_{1}^{2}}/M$

同时在推导过程中，表面态还有以下限制：

$k_{x}^{2}+k_{z}^{2}+2ak_x<k_{w}^{2}$

其中， $a \equiv AD_1/2M\sqrt{M^2-D_{1}^{2}}$

从表面态哈密顿量可以看出，这时候给定一个费米能，表面态不再是一个线段，而是在限制条件下的一段曲线，称为费米弧。

参考文献：

[1] High-field magnetoconductivity of topological semimetals with short-range potential

[2] Linear magnetoconductivity in an intrinsic topological Weyl semimetal

[3] Dispersion of Fermi arcs in Weyl semimetals and their evolutions to Dirac cones

[4] 3D Quantum Hall Effect of Fermi Arcs in Topological Semimetals

4,652 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

10 thoughts on “外尔半金属的哈密顿量和费米弧（附Python代码）”

老师如果这个哈密顿量里面包含了单位矩阵怎么表示好？

guanjihuan说道：

2023年4月4日 17:04

python中用np.eye(2)或np.identity(2)

回复

博主，您好，我最近在重复您的参考文献中的第四篇，三维量子霍尔效应那篇，遇到了一些问题。就是当哈密顿量在ky方向和kz方向都开了边界，都用方势阱的基去展开，然后解出kx的色散关系后，我想看y方向的波函数（文献中Fig1.(i)图），这个时候我用eig(H)求出了展开系数，要投影到基矢上，y方向的基矢很清晰，不同的y对应了一套完整的方势阱基矢，问题是z方向的基矢我不知道该怎么取，因为我想看的是y方向的波函数

guanjihuan说道：

2023年3月14日 15:03

文献中说的是：“The energies deform into edge states near z0 = \pm 100 nm”，选取了某个z值。其实也可以看y-z二维波函数分布。

回复

博主:
你知道外尔半金属费米波矢与费米能之间的关系么？

guanjihuan说道：

2022年10月7日 06:14

你说的就是能带吧，为基于两个外尔点的狄拉克锥状的关系。

回复

博主您知道这个weyl半金属最小模型是怎么推导出来的吗？

guanjihuan说道：

2021年8月15日 14:57

从狄拉克方程可以推导出外尔费米子的方程，描述的是外尔费米子的基本性质。

回复

博主，你好。我有一个问题，你画费米面的那个图，kx和kz的方向是不是反了呀。对于给定的kz，Hamilton量不是和kx成正比吗，但图中好像是反过来的。

guanjihuan说道：

2021年3月23日 19:58

是和kx成正比，图画的也没错，只是在三维中看起来容易看错。可以自己画出来，在三维空间转一转。实际上应该画成彩色或者有渐变的可能会更直观些。已经把图做了修改。

回复

外尔半金属的哈密顿量和费米弧（附Python代码）

1. 外尔半金属能带

2. 外尔半金属的费米弧

3. 外尔半金属哈密顿量的另外一个形式

Published by guanjihuan

10 thoughts on “外尔半金属的哈密顿量和费米弧（附Python代码）”

发表评论取消回复

1. 外尔半金属能带

2. 外尔半金属的费米弧

3. 外尔半金属哈密顿量的另外一个形式

Published by guanjihuan

10 thoughts on “外尔半金属的哈密顿量和费米弧（附Python代码）”

发表评论 取消回复

发表评论取消回复