石墨烯示意图:
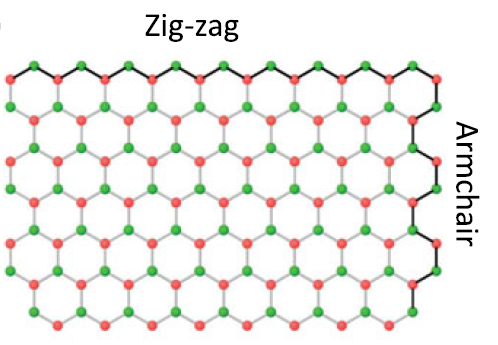
该图片来源于Hideo Aoki Mildred S. Dresselhaus的“Physics of Graphene”
只考虑最近邻跃迁t=1。以下是画二维石墨烯能带的代码:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/408
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import functools
def hamiltonian(k1, k2, M, t1, a=1/sqrt(3)): # graphene哈密顿量(a为原子间距,不赋值的话默认为1/sqrt(3))
# 初始化为零矩阵
h0 = np.zeros((2, 2), dtype=complex)
h1 = np.zeros((2, 2), dtype=complex)
# 质量项(mass term),用于打开带隙
h0[0, 0] = M
h0[1, 1] = -M
# 最近邻项
h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h1[0, 1] = h1[1, 0].conj()
# # 最近邻项也可写成这种形式
# h1[1, 0] = t1+t1*cmath.exp(1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)+t1*cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)
# h1[0, 1] = h1[1, 0].conj()
matrix = h0 + h1
return matrix
def main():
hamiltonian0 = functools.partial(hamiltonian, M=0, t1=1, a=1/sqrt(3)) # 使用偏函数,固定一些参数
k1 = np.linspace(-2*pi, 2*pi, 500)
k2 = np.linspace(-2*pi, 2*pi, 500)
plot_bands_two_dimension(k1, k2, hamiltonian0)
def plot_bands_two_dimension(k1, k2, hamiltonian):
from matplotlib import cm
dim = hamiltonian(0, 0).shape[0]
dim1 = k1.shape[0]
dim2 = k2.shape[0]
eigenvalue_k = np.zeros((dim2, dim1, dim))
i0 = 0
for k10 in k1:
j0 = 0
for k20 in k2:
matrix0 = hamiltonian(k10, k20)
eigenvalue, eigenvector = np.linalg.eig(matrix0)
eigenvalue_k[j0, i0, :] = np.sort(np.real(eigenvalue[:]))
j0 += 1
i0 += 1
fig = plt.figure()
ax = fig.gca(projection='3d')
k1, k2 = np.meshgrid(k1, k2)
for dim0 in range(dim):
ax.plot_surface(k1, k2, eigenvalue_k[:, :, dim0], rcount=200, ccount=200, cmap=cm.coolwarm, linewidth=0, antialiased=False)
plt.show()
if __name__ == '__main__':
main()
能带图为:
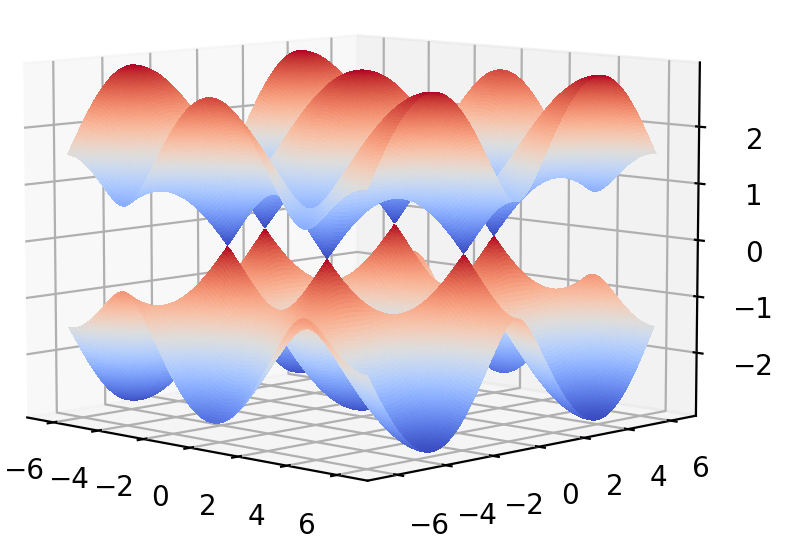
下面考虑准一维的情况( 这里只考虑Zigzag边的石墨烯条带)。
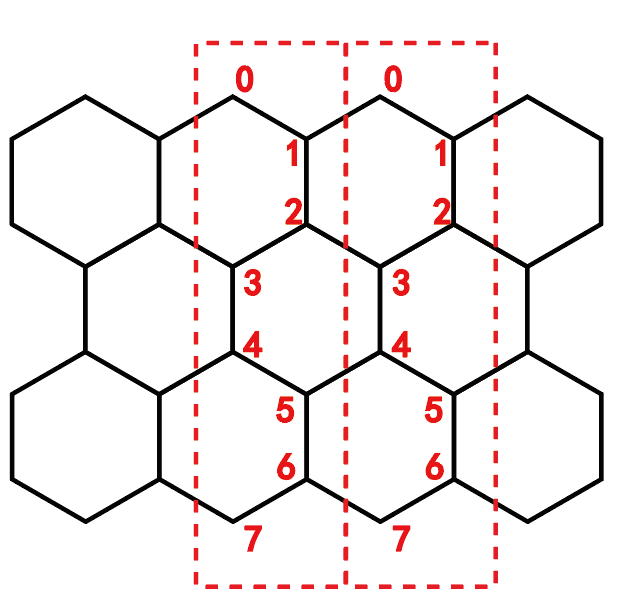
在我自己写的代码里,原子的编号方式如下图所示。按既定规则,把元胞内的跃迁矩阵h00写和元胞间的跃迁矩阵h01都写出来,包括所有的最近邻跃迁, 然后整体傅里叶变换即可。关于离散傅里叶变换可参考博文:离散格子的傅里叶变换和反傅里叶变换 。这里是以元胞为单元(红色虚线圈了两个元胞作为例子),在一个方向做傅里叶变换转到倒空间(k空间),求本征值后就可以找到k与能量E的关系,即能带。
以下是代码:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/408
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import functools
def hamiltonian(k, N, M, t1): # graphene哈密顿量(N是条带的宽度参数)
# 初始化为零矩阵
h00 = np.zeros((4*N, 4*N), dtype=complex)
h01 = np.zeros((4*N, 4*N), dtype=complex)
# 原胞内的跃迁h00
for i in range(N):
h00[i*4+0, i*4+0] = M
h00[i*4+1, i*4+1] = -M
h00[i*4+2, i*4+2] = M
h00[i*4+3, i*4+3] = -M
# 最近邻
h00[i*4+0, i*4+1] = t1
h00[i*4+1, i*4+0] = t1
h00[i*4+1, i*4+2] = t1
h00[i*4+2, i*4+1] = t1
h00[i*4+2, i*4+3] = t1
h00[i*4+3, i*4+2] = t1
for i in range(N-1):
# 最近邻
h00[i*4+3, (i+1)*4+0] = t1
h00[(i+1)*4+0, i*4+3] = t1
# 原胞间的跃迁h01
for i in range(N):
# 最近邻
h01[i*4+1, i*4+0] = t1
h01[i*4+2, i*4+3] = t1
matrix = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
return matrix
def main():
hamiltonian0 = functools.partial(hamiltonian, N=40, M=0, t1=1)
k = np.linspace(-pi, pi, 300)
plot_bands_one_dimension(k, hamiltonian0)
def plot_bands_one_dimension(k, hamiltonian):
dim = hamiltonian(0).shape[0]
dim_k = k.shape[0]
eigenvalue_k = np.zeros((dim_k, dim))
i0 = 0
for k0 in k:
matrix0 = hamiltonian(k0)
eigenvalue, eigenvector = np.linalg.eig(matrix0)
eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
i0 += 1
for dim0 in range(dim):
plt.plot(k, eigenvalue_k[:, dim0], '-k')
plt.show()
if __name__ == '__main__':
main()
这是画出的能带图:
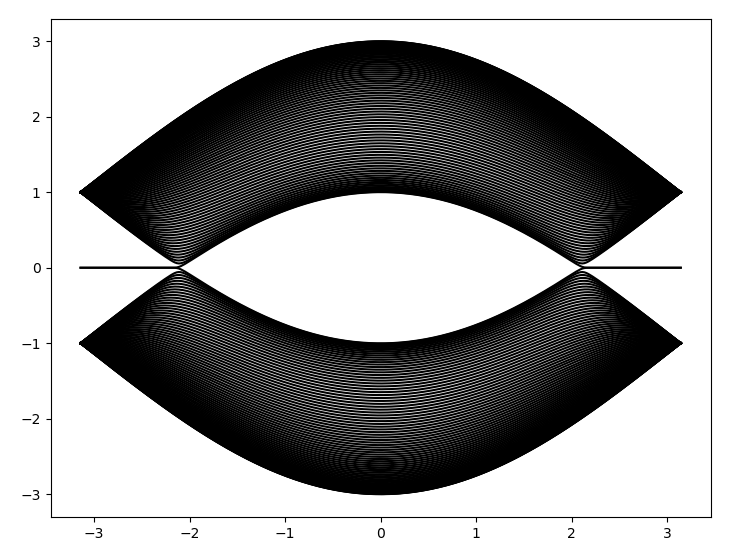
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
eigenvalue_k[j0, i0, :] = np.sort(np.real(eigenvalue[:]))
想问一下为什么这段是要实值而非平方根呢?
误* 想说绝对值/与共轭相乘的平方根
因为定态薛定谔方程的本征值为能量。我不知道你说的是什么意思。
我的意思是,用np.linage.eig求出来的本征值是复数,为什么要用np.real截取其中实数部分而非用np.abs得到绝对值呢(按理来说,求本征值应该算出来的都是实数,±根号下互共轭的最近邻项相乘)
嗯,如果是厄米系统的哈密顿量(厄米矩阵),那么本征值一定是实数,所以这里直接把数值计算中的无穷小量的虚部扔掉了,在这种情况下用np.real和np.abs都是可以的。
2D模型中,代码57行:ax = fig.gca(projection='3d')随着matplot更新已经不可用了,可以用下面替换:
ax = fig.add_subplot(projection = '3d')
嗯,感谢告知!由于使用版本不同的原因,目前我在博文中我暂时不做修改,可能后续使用新版本时会改过来。
请问for i in range(N-1):
# 最近邻
h00[i*4+3, (i+1)*4+0] = t1
h00[(i+1)*4+0, i*4+3] = t1这个部分的意思。在原胞内没找到对应
在程序中,元胞内四个为一个单位,一个单位内的最近邻跃迁前面已经赋值了,但相邻单位之间还需要连接起来,这里的代码就是起到连接的作用,也是最近邻跃迁。
好的,非常感谢!
您好,想问一下这里的质量项是怎么来的呢?是考虑了次近邻的结果吗,考虑次近邻A to A和B to B不同的相位所以一个是+M一个是-M?
不是的,质量项就是势能项,只是这里是交错势能,不同子格不一样。
博主你好,请问有matlab的代码吗?
目前是没整理。python和matlab在写的时候要注意区别:python下标从0开始,matlab从1开始。关于求本征值和画图,python和matlab各有书写的方法。你可以试着自己改写成matlab代码,或者让ChatGPT帮忙改写后再自己检查下。
好的 谢谢
不知道是哪里出了问题,运行的结果在接近-pi和pi的时候图像不太对
h01少了一撇。这句改成:hh=h00+h01*exp(1i*kx(i))+h01'*exp(-1i*kx(i));
在Matlab中,一撇等于转置加共轭,即Python中的.transpose().conj()。
谢谢你
请问下博主,在zigzag模型中,哈密顿量中如果有kx,ky两个,那应该怎么写
zigzag石墨烯条带是准一维体系,只有一个方向有k,为无限长。还有一个方向是有限宽度,因此不可能同时有kx和ky。
想问一下博主,为什么第一个程序里面不用写 原胞间的跃迁项h01矩阵,而第二个程序里面需要构造h01*cmath.exp(1j*k) 呢?
第一个程序的哈密顿量已经是倒空间的形式了,因此不需要傅里叶变换,或者说是已经做完傅里叶变换。第二个程序是从实空间出发,写出条带的元胞,然后是按准一维条带进行傅里叶变换,得到倒空间的哈密顿量。参考:离散格子的傅里叶变换和反傅里叶变换。
博主你好,我问一个简单的问题,为什么zigzag边界的计算和你之前那个准一维的计算过程差不多?这个结构胞间和胞内的跃迁都是有斜线的,不需要考虑矢量问题吗?
如果是以原子进行傅里叶变换,傅里叶变换产生的相位是需要考虑在x方向的投影。但如果是以元胞进行傅里叶变换,类似于一维原子链,其他为内部自由度。折线结构已经体现在hopping上了。
所以在写hamiltonian 的h01[4 i +0, 4 i +1]这一项的时候,应该是: t(1+exp(i k A); 而不应该是: t(1+exp(i k A* \sqrt{3}/2);
想问一下博主是这样么;A对应的应该是超胞的晶格常数,A=\sqrt{3} a;
a是石墨烯单元的两原子间距;
实际上在楼主代码里面A默认是1;而并非a默认是1;
请问博主大哥哥,我的理解对么
跟同学讨论过了,hamiltonian 的h01[4 i +0, 4 i +1]这一项,应该是: t(1+exp(i k A); 而不应该是: t(1+exp(i k A* \sqrt{3}/2);
括号中没有1吧。代码中是这个:matrix = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)。
您这边说的斜线结构体现在hopping意思指的是代码注释中的原胞间的hopping吧
就是这块,
# 原胞间的跃迁h01
for i in range(N):
# 最近邻
h01[i*4+1, i*4+0] = t1
h01[i*4+2, i*4+3] = t1
因为这里只有0--1 2--3,没有1--2。是这个意思吗?
如果∠012不是120度是其他角度,是不是对于准一维来说没有区别啊?
嗯,是这个意思。哈密顿量没有直接的角度信息,但角度这个物理信息已经通过所有的hopping项来体现了。不同的结构有不同的hopping项,区别是在这里。
不好意思,我问一个很trivial的问题,您这里要计算zigzag的边缘态,但是您画的红色的条带里面难道不是armchair型的么?所谓原胞内原子数是4N是怎么理解呢?zigzag边缘不就考虑相邻两个原子之间的hopping就可以了么?
嗯,这里我图标明的不是太完整。示意图水平方向是无限长的,垂直方向是有限宽度的,红色圈出来的不是条带,是表示元胞,边缘是zigzag型的。
因为4个原子重复一次,所以在写程序时,我就按4的倍数来写循环了。
有连接的地方都要写上hopping。
请问,我类推到armchair纳米带的方法,出来的图像大相径庭呢?
所以请教博主。
armchair的能带和zigzag的能带本身就是不一样的。我也不确定你写的对不对。你可以找armchair石墨烯的一些文章或者综述,应该有挺多的,看是否能重复对应的图。
稍微看了一点点,第一块最近邻的第三行就有错误:h0(i*4+1,i*4+1) = t1。有需要可加我微信讨论,我的联系方式在:https://www.guanjihuan.com/about
博主可以讲一下Armchair型边界的思路吗?应该选取什么样形状做元胞。
画出来后,找条带的最小重复单元。怎么选取都可以,只要是最小单元,同一个体系计算出的能带应该都是一样的。
想问下博主,这个质量项代表什么呀,科研新手,有点不太明白,谢谢啦
# 质量项(mass term), 用于打开带隙
h0[0, 0] = M
h0[1, 1] = -M
其实就是交错势(staggered potential),一般写成$m*\sigma_z$。至于为什么称为质量项(mass term),我也不是很清楚,但文献中都是这么使用的。我猜可能是因为这里的m会使得能带打开带隙,而对于有带隙的体系,大多数时候电子是存在有效质量的,所以称为质量项,不是很严谨。不一定是这样的,有需要可以找找看有没有文献中提到这个,我目前是没看到。
好的 谢谢啦
请问二维蜂窝晶格实空间的能谱图该怎么画呢。如果论文给出是32×26lattice,全基失该怎么定义
编号后写哈密顿量,然后直接对角化就行了。可能会没有太大规律,需要手动一一赋值,不能用循环赋值。参考:方格子模型在实空间中的哈密顿量形式。