施密特正交化(Schmidt orthogonalization)过程[1]:
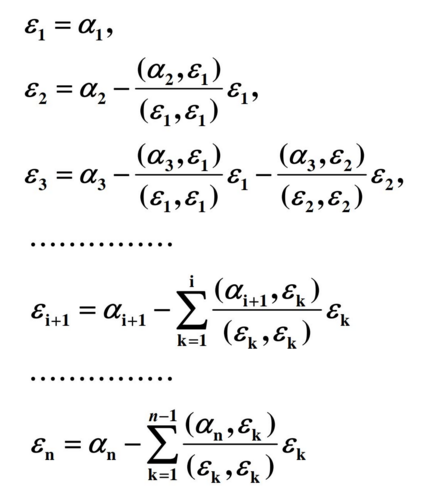
Python代码:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/10890
"""
import numpy as np
def main():
A = np.array([[0, 1, 1, -1], [1, 0, -1, 1], [1, -1, 0, 1], [-1, 1, 1, 0]])
eigenvalue, eigenvector = np.linalg.eig(A)
print('矩阵:\n', A)
print('特征值:\n', eigenvalue)
print('特征向量:\n', eigenvector)
print('\n判断是否正交:\n', np.dot(eigenvector.transpose(), eigenvector))
print('判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose()))
print('对角化验证:')
print(np.dot(np.dot(eigenvector.transpose(), A), eigenvector))
# 施密斯正交化
eigenvector = Schmidt_orthogonalization(eigenvector)
print('\n施密斯正交化后,特征向量:\n', eigenvector)
print('施密斯正交化后,判断是否正交:\n', np.dot(eigenvector.transpose(), eigenvector))
print('施密斯正交化后,判断是否正交:\n', np.dot(eigenvector, eigenvector.transpose()))
print('施密斯正交化后,对角化验证:')
print(np.dot(np.dot(eigenvector.transpose(), A), eigenvector))
def Schmidt_orthogonalization(eigenvector):
num = eigenvector.shape[1]
for i in range(num):
for i0 in range(i):
eigenvector[:, i] = eigenvector[:, i] - eigenvector[:, i0]*np.dot(eigenvector[:, i].transpose().conj(), eigenvector[:, i0])/(np.dot(eigenvector[:, i0].transpose().conj(),eigenvector[:, i0]))
eigenvector[:, i] = eigenvector[:, i]/np.linalg.norm(eigenvector[:, i])
return eigenvector
if __name__ == '__main__':
main()运行结果:
矩阵:
[[ 0 1 1 -1]
[ 1 0 -1 1]
[ 1 -1 0 1]
[-1 1 1 0]]
特征值:
[ 1. -3. 1. 1.]
特征向量:
[[ 0.8660254 0.5 0.12803516 0.08530895]
[ 0.28867513 -0.5 0.85020245 -0.16863006]
[ 0.28867513 -0.5 -0.36108364 0.80962746]
[-0.28867513 0.5 0.36108364 0.55568845]]
判断是否正交:
[[ 1.00000000e+00 5.55111512e-17 1.47842273e-01 9.85062898e-02]
[ 5.55111512e-17 1.00000000e+00 5.55111512e-17 -5.55111512e-17]
[ 1.47842273e-01 5.55111512e-17 1.00000000e+00 -2.24140369e-01]
[ 9.85062898e-02 -5.55111512e-17 -2.24140369e-01 1.00000000e+00]]
判断是否正交:
[[ 1.02367062 0.09447016 0.02283706 0.0936366 ]
[ 0.09447016 1.08461363 -0.11018839 -0.12004491]
[ 0.02283706 -0.11018839 1.11921136 -0.0138141 ]
[ 0.0936366 -0.12004491 -0.0138141 0.77250439]]
对角化验证:
[[ 1.00000000e+00 -1.66533454e-16 1.47842273e-01 9.85062898e-02]
[-2.22044605e-16 -3.00000000e+00 -2.22044605e-16 0.00000000e+00]
[ 1.47842273e-01 -1.66533454e-16 1.00000000e+00 -2.24140369e-01]
[ 9.85062898e-02 1.11022302e-16 -2.24140369e-01 1.00000000e+00]]
施密斯正交化后,特征向量:
[[ 8.66025404e-01 5.00000000e-01 4.20959579e-17 -3.85081968e-18]
[ 2.88675135e-01 -5.00000000e-01 8.16496581e-01 2.87496183e-17]
[ 2.88675135e-01 -5.00000000e-01 -4.08248290e-01 7.07106781e-01]
[-2.88675135e-01 5.00000000e-01 4.08248290e-01 7.07106781e-01]]
施密斯正交化后,判断是否正交:
[[1.00000000e+00 0.00000000e+00 4.16333634e-17 0.00000000e+00]
[0.00000000e+00 1.00000000e+00 2.77555756e-17 0.00000000e+00]
[4.16333634e-17 2.77555756e-17 1.00000000e+00 0.00000000e+00]
[0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
施密斯正交化后,判断是否正交:
[[ 1.00000000e+00 8.32667268e-17 0.00000000e+00 0.00000000e+00]
[ 8.32667268e-17 1.00000000e+00 0.00000000e+00 2.77555756e-17]
[ 0.00000000e+00 0.00000000e+00 1.00000000e+00 -8.32667268e-17]
[ 0.00000000e+00 2.77555756e-17 -8.32667268e-17 1.00000000e+00]]
施密斯正交化后,对角化验证:
[[ 1.00000000e+00 -2.22044605e-16 4.16333634e-17 2.77555756e-17]
[-1.11022302e-16 -3.00000000e+00 -1.11022302e-16 0.00000000e+00]
[ 5.55111512e-17 -5.55111512e-17 1.00000000e+00 5.55111512e-17]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]另外,这里给的函数可能还不一定稳定,目前还不清楚是什么原因。一个例子为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/10890
"""
import numpy as np
a = [[ 0 , 0 , 1.5 , 0.32635182-0.98480775j],
[0 , 0 , -0.32635182-0.98480775j, 1.5 ],
[ 1.5 , -0.32635182+0.98480775j ,0, 0 ],
[ 0.32635182+0.98480775j , 1.5 , 0, 0 ]]
def Schmidt_orthogonalization(eigenvector):
num = eigenvector.shape[1]
for i in range(num):
for i0 in range(i):
eigenvector[:, i] = eigenvector[:, i] - eigenvector[:, i0]*np.dot(eigenvector[:, i].transpose().conj(), eigenvector[:, i0])/(np.dot(eigenvector[:, i0].transpose().conj(),eigenvector[:, i0]))
eigenvector[:, i] = eigenvector[:, i]/np.linalg.norm(eigenvector[:, i])
return eigenvector
def verify_orthogonality(vectors):
identity = np.eye(vectors.shape[1])
product = np.dot(vectors.T.conj(), vectors)
return np.allclose(product, identity)
# 对 np.linalg.eigh() 的特征向量正交化
E, v = np.linalg.eigh(a)
print(verify_orthogonality(v))
v1 = Schmidt_orthogonalization(v)
print(verify_orthogonality(v1))
from scipy.linalg import orth
v2 = orth(v)
print(verify_orthogonality(v2))
v3, S, Vt = np.linalg.svd(v)
print(verify_orthogonality(v3))
v4, R = np.linalg.qr(v)
print(verify_orthogonality(v4))
print()
# 对 np.linalg.eig() 的特征向量正交化
E, v = np.linalg.eig(a)
print(verify_orthogonality(v))
v1 = Schmidt_orthogonalization(v)
print(verify_orthogonality(v1))
from scipy.linalg import orth
v2 = orth(v)
print(verify_orthogonality(v2))
v3, S, Vt = np.linalg.svd(v)
print(verify_orthogonality(v3))
v4, R = np.linalg.qr(v)
print(verify_orthogonality(v4))运行结果为:
True
True
True
True
True
False
False
True
True
True说明:这里的例子 np.linalg.qr() 、np.linalg.svd() 和 scipy.linalg.orth() 都成功完成了正交化,但自定义的 Schmidt_orthogonalization() 函数没有完成正交化,暂时不知道是什么原因导致的。个人比较推荐使用 np.linalg.qr(),有时候 np.linalg.svd() 和 scipy.linalg.orth() 在解决实际的物理问题时可能也会出现问题。
可能的原因是:对于有些例子,矩阵中的特征向量非常接近线性相关,那么导致了某些算法在数值计算上不是很稳定,在具体应用时可以考虑使用多个算法进行计算对比。
参考资料:
[1] 截图自北京科技大学廖福成老师的”高等代数与解析几何“课件
[2] ”高等代数与解析几何“、”线性代数“、”高等数学“等相关教材
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】