在二维平面模拟三体运动（附Python代码）

发布时间：2019年11月3日2024年6月6日

最近修改时间：2024年6月6日

三体一般来说没有解析解，只有几个特殊的初始条件才有解析解。数值解相对来说就比较简单了，只要套用万有引力公式即可，于是就试着写了下。这篇只考虑在二维平面上的情况，一是画图会比较简单，二是观看动画时不会显得太乱。其实，在二维平面上，已经就可以看到三体运动轨迹的复杂性了。一般来说，如果初始速度为零，在万有引力的作用下，三体的运动轨迹就是在一个平面内（这里给的程序可以修改初始速度，但也只是考虑在平面内的初速度）。

“数值解的误差也受计算步长的影响，计算步长越小越精确，但是因为数据一定会有精度，并不能真正的无穷小，所以实际上在时间足够长以后依旧会产生很大的误差”[1]。

说明：这边代码不是实时预览的。因为一次的计算时长比较长，所以直接保存为JPG图片或GIF动画文件会更好些。其实更好的数据保存格式应该是文本格式，保存所有计算结果的坐标，之后如果需要修改动画样式时，可以不需要重新计算。

目录隐藏

1. 三体的质量相差不大的情况

2. 考虑其中有一个球相对较大的情况

3. 某个球修改为大质量，模拟恒星-行星系统

1. 三体的质量相差不大的情况

代码如下（初始条件可以修改。这里的步长设为0.1秒，如果缩小步长，过一段时间后轨迹会完全不同，步长越小越精确）。

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/858
"""

import numpy as np
import matplotlib.pyplot as plt
import os
# os.chdir('E:/data')  # 设置路径

# 万有引力常数
G = 1

# 三体的质量
m1 = 15  # 绿色
m2 = 12  # 红色
m3 = 8  # 蓝色

# 三体的初始位置
x1 = 300  # 绿色
y1 = 50
x2 = -100  # 红色
y2 = -200
x3 = -100  # 蓝色
y3 = 150

# 三体的初始速度
v1_x = 0  # 绿色
v1_y = 0
v2_x = 0  # 红色
v2_y = 0
v3_x = 0  # 蓝色
v3_y = 0

# 步长
t = 0.1

plt.ion()  # 开启交互模式
observation_max = 100  # 视线范围初始值
x1_all = [x1]  # 轨迹初始值
y1_all = [y1]
x2_all = [x2]
y2_all = [y2]
x3_all = [x3]
y3_all = [y3]

i0 = 0
for i in range(1000000):  
    distance12 = np.sqrt((x1-x2)**2+(y1-y2)**2)   # 物体1和物体2之间的距离
    distance13 = np.sqrt((x1-x3)**2+(y1-y3)**2)   # 物体1和物体3之间的距离
    distance23 = np.sqrt((x2-x3)**2+(y2-y3)**2)   # 物体2和物体3之间的距离
    
    # 对物体1的计算
    a1_2 = G*m2/(distance12**2)  # 物体2对物体1的加速度（用上万有引力公式）
    a1_3 = G*m3/(distance13**2)  # 物体3对物体1的加速度
    a1_x = a1_2*(x2-x1)/distance12 + a1_3*(x3-x1)/distance13  # 物体1受到的水平加速度
    a1_y = a1_2*(y2-y1)/distance12 + a1_3*(y3-y1)/distance13  # 物体1受到的垂直加速度
    v1_x = v1_x + a1_x*t  # 物体1的速度
    v1_y = v1_y + a1_y*t  # 物体1的速度
    x1 = x1 + v1_x*t  # 物体1的水平位置
    y1 = y1 + v1_y*t  # 物体1的垂直位置
    x1_all = np.append(x1_all, x1)  # 记录轨迹
    y1_all = np.append(y1_all, y1)  # 记录轨迹
    
    # 对物体2的计算
    a2_1 = G*m1/(distance12**2)
    a2_3 = G*m3/(distance23**2)
    a2_x = a2_1*(x1-x2)/distance12 + a2_3*(x3-x2)/distance23
    a2_y = a2_1*(y1-y2)/distance12 + a2_3*(y3-y2)/distance23
    v2_x = v2_x + a2_x*t
    v2_y = v2_y + a2_y*t
    x2 = x2 + v2_x*t
    y2 = y2 + v2_y*t
    x2_all = np.append(x2_all, x2)
    y2_all = np.append(y2_all, y2)
    
    # 对物体3的计算
    a3_1 = G*m1/(distance13**2)
    a3_2 = G*m2/(distance23**2)
    a3_x = a3_1*(x1-x3)/distance13 + a3_2*(x2-x3)/distance23
    a3_y = a3_1*(y1-y3)/distance13 + a3_2*(y2-y3)/distance23
    v3_x = v3_x + a3_x*t
    v3_y = v3_y + a3_y*t
    x3 = x3 + v3_x*t
    y3 = y3 + v3_y*t
    x3_all = np.append(x3_all, x3)
    y3_all = np.append(y3_all, y3)

    # 选择观测坐标
    axis_x = np.mean([x1, x2, x3])  # 观测坐标中心固定在平均值的地方
    axis_y = np.mean([y1, y2, y3])  # 观测坐标中心固定在平均值的地方
    while True:
        if np.abs(x1-axis_x) > observation_max or np.abs(x2-axis_x) > observation_max or np.abs(x3-axis_x) > observation_max or\
        np.abs(y1-axis_y) > observation_max or np.abs(y2-axis_y) > observation_max or np.abs(y3-axis_y) > observation_max:
            observation_max = observation_max * 2  # 有一个物体超出视线时，视线范围翻倍
        elif np.abs(x1-axis_x) < observation_max/10 and np.abs(x2-axis_x) < observation_max/10 and np.abs(x3-axis_x) < observation_max/10 and\
        np.abs(y1-axis_y) < observation_max/10 and np.abs(y2-axis_y) < observation_max/10 and np.abs(y3-axis_y) < observation_max/10:
            observation_max = observation_max / 2   # 所有物体都在的视线的10分之一内，视线范围减半
        else:
            break

    plt.axis([axis_x-observation_max, axis_x+observation_max, axis_y-observation_max,  axis_y+observation_max])
    
    plt.plot(x1, y1, 'og', markersize=m1*100/observation_max)  # 默认密度相同，质量越大的，球面积越大。视线范围越宽，球看起来越小。
    plt.plot(x2, y2, 'or', markersize=m2*100/observation_max) 
    plt.plot(x3, y3, 'ob', markersize=m3*100/observation_max)
    plt.plot(x1_all, y1_all, '-g')  # 画轨迹
    plt.plot(x2_all, y2_all, '-r')
    plt.plot(x3_all, y3_all, '-b')

    # plt.show()  # 显示图像
    # plt.pause(0.00001)  # 暂停0.00001，防止画图过快

    if np.mod(i, 500) == 0:  # 当运动明显时，把图画出来
        print(i0)
        plt.savefig(str(i0)+'.jpg')  # 保存为图片可以用来做动画
        i0 += 1
    plt.clf()   # 清空

步长为0.1时，运行结果为：

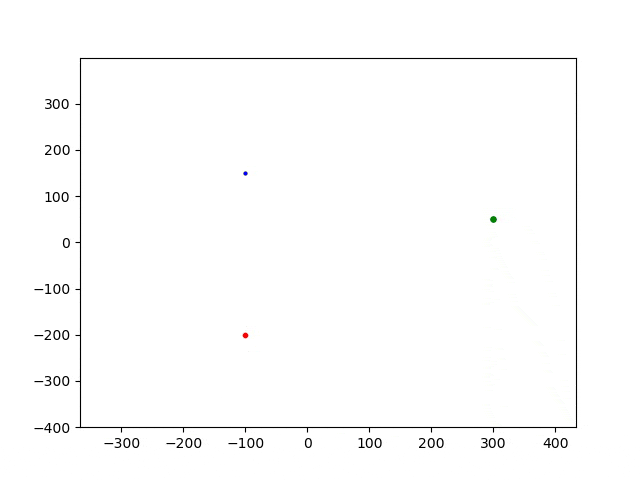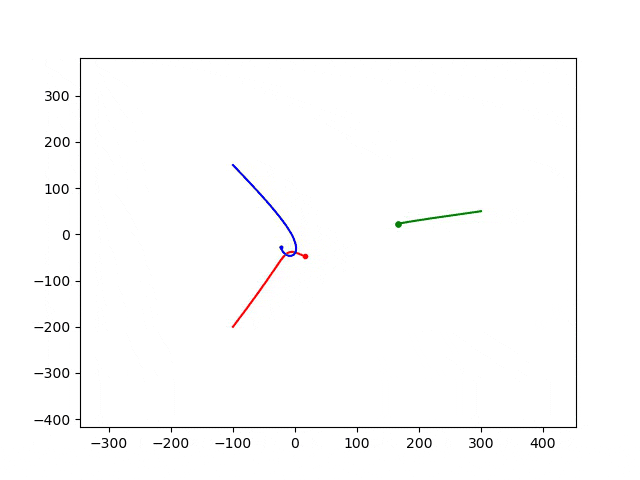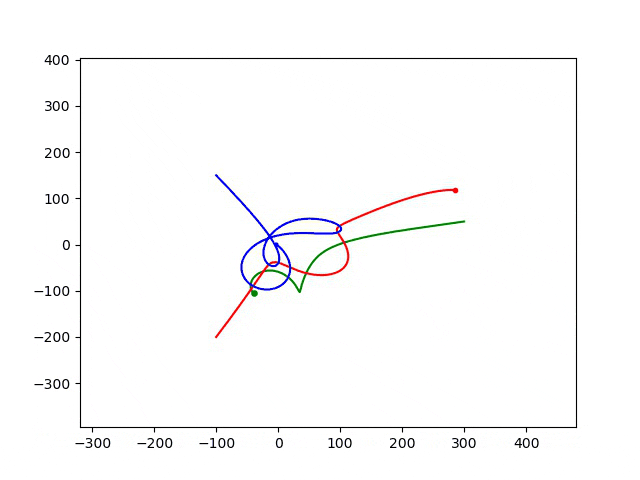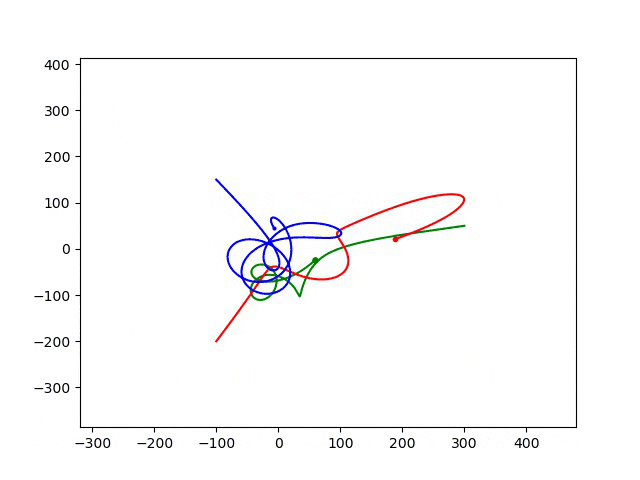
步长为0.05，运行结果为：

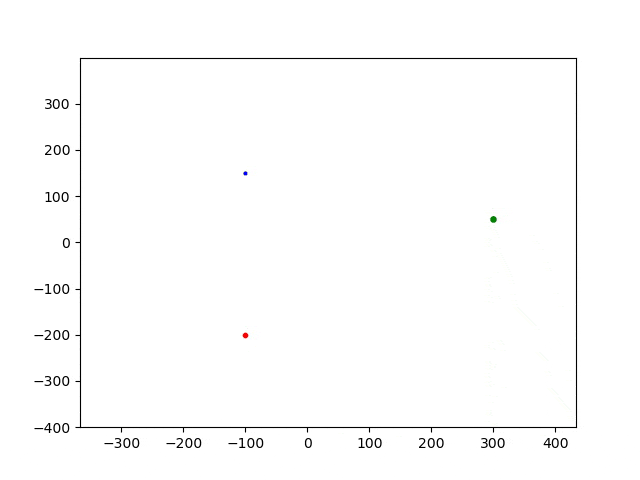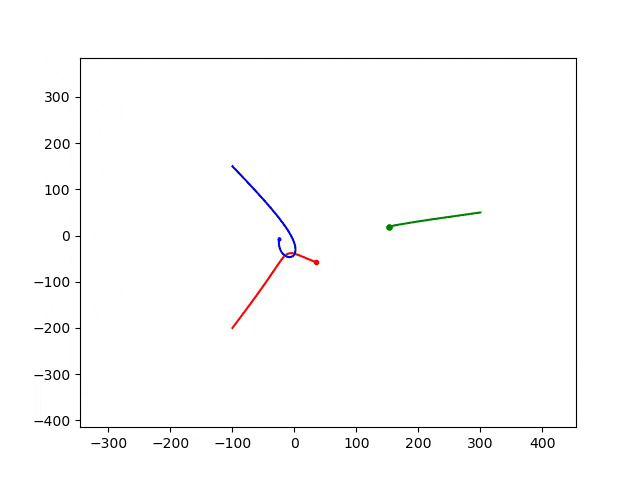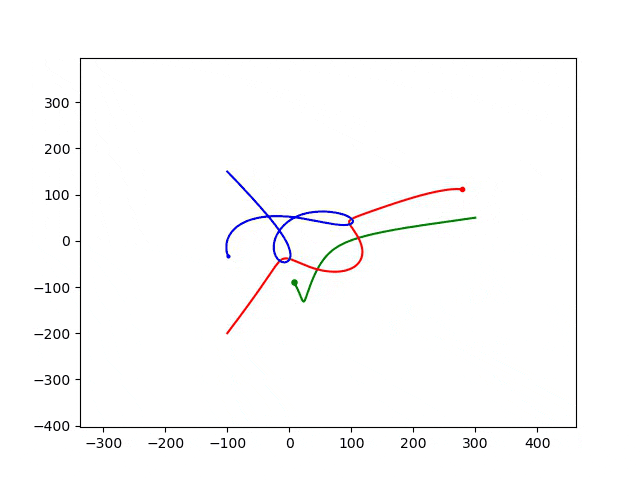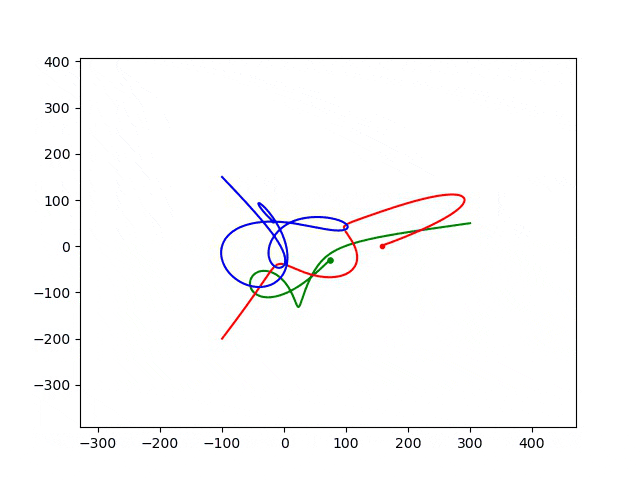
可以看出：随着步长减小，运动轨迹发生了变化。实际的物理运动路径应该是步长小的计算结果。

2. 考虑其中有一个球相对较大的情况

参数为：

# 三体的质量
m1 = 3  # 绿色
m2 = 100  # 红色
m3 = 10  # 蓝色

# 三体的初始位置
x1 = 0 # 绿色
y1 = -100
x2 = 0  # 红色
y2 = 0
x3 = 0  # 蓝色
y3 = 50

# 三体的初始速度
v1_x = 1  # 绿色
v1_y = 0
v2_x = 0  # 红色
v2_y = 0
v3_x = 2  # 蓝色
v3_y = 0

步长为0.1时，结果为：

步长为0.05时，结果为：

选取两种步长，前面运动轨迹基本上相同。当误差逐步积累到一定程度时，轨迹则变得完全不同。

3. 某个球修改为大质量，模拟恒星-行星系统

参数为：

# 三体的质量
m1 = 10  # 绿色
m2 = 1000  # 红色
m3 = 10  # 蓝色

# 三体的初始位置
x1 = 0  # 绿色
y1 = 500
x2 = 0  # 红色
y2 = 0
x3 = 0 # 蓝色
y3 = 1000

# 三体的初始速度
v1_x = 1.5  # 绿色
v1_y = 0
v2_x = 0  # 红色
v2_y = 0
v3_x = 0.8  # 蓝色
v3_y = 0

步长为0.1时，结果为：

步长为0.05时，结果略。

更多参数的情况可以自行计算，计算还是挺费时间的，一个动图的时间都是一小时以上。关于相撞问题，直观感觉是：在某些条件下，三体会发生相撞，而在另外某些条件下，则永不发生相撞，即三体的稳定性问题。这个问题具体没有研究过，这里只是把三体当成质点，考虑没有体积或者体积很小的情况，不考虑相撞的问题。

制作动画的代码如下：

import imageio
import numpy as np
import os
# os.chdir('E:/data')  # 设置文件读取和保存位置

images = []
for i in range(1000):
    image = str(i)+'.jpg'
    im = imageio.imread(image)
    images.append(im)
imageio.mimsave("a.gif", images, 'GIF', duration=0.1)  # durantion是延迟时间

运行该代码把上面代码生成保存的.jpg图片制作成动画.gif。

制作完GIF之后可以用网站 https://www.iloveimg.com/zh-cn 或其他网站/软件把.gif图像压缩成更小的体积。一个开源软件可参考：FFmpeg的下载和使用（媒体文件的格式转换和压缩等）。画质会在一定程度上会变差，可根据需要进行压缩。

参考资料：

[1] https://www.jianshu.com/p/d1a56bf54a6c

11,701 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

32 thoughts on “在二维平面模拟三体运动（附Python代码）”

匿名说道：

2024年11月7日 08:30

是的是的，我看的时候也有这个疑惑，应该要用”old“的值，不然1，2，3的运动就不平权了。

回复
1. guanjihuan说道：
  
  2024年11月7日 17:57
  
  嗯，在每一个时刻都重新计算一次。
  
  回复

简单修改了一下，代码可读性较差勿喷

1.防止 x_all 等列表在计算后期变得很大，容易爆内存

2.实现了用 txt 存储计算过程的代码

3.计算时间剩余进度条

4.将计算时间减小到1/10

计算程序：
```python


import numpy as np
import matplotlib.pyplot as plt
import os
import time

os.chdir('E:/three-body/data')  # 设置路径
draw = False

# 万有引力常数
G = 1

# 三体的质量
m1 = 15  # 绿色
m2 = 12  # 红色
m3 = 8  # 蓝色

# 三体的初始位置
x1 = 300  # 绿色
y1 = 50
x2 = -100  # 红色
y2 = -200
x3 = -100  # 蓝色
y3 = 150

# 三体的初始速度
v1_x = 0  # 绿色
v1_y = 0
v2_x = 0  # 红色
v2_y = 0
v3_x = 0  # 蓝色
v3_y = 0

# 步长
#####
t = 0.1
i0 = 0
ranges = 20000
save_r = 100


plt.ion()  # 开启交互模式
observation_max = 100  # 视线范围初始值
x1_all = [x1]  # 轨迹初始值
y1_all = [y1]
x2_all = [x2]
y2_all = [y2]
x3_all = [x3]
y3_all = [y3]

with open("log.txt", "w", encoding="UTF-8") as file:
    lt = time.localtime()
    file.write(str(m1)+'\n')
    file.write(str(m2)+'\n')
    file.write(str(m3)+'\n')

    file.write((f"{lt.tm_year}.{lt.tm_mon}.{lt.tm_mday} {lt.tm_hour}:{lt.tm_min}:{lt.tm_sec} "
                f"{['Monday','Tuesday','Wednesday','Thursday','Friday','Saturday','Sunday'][lt.tm_wday]}\n"))

start_time = time.time()
time1 = start_time

for i in range(ranges):
    if True:
        distance12 = np.sqrt((x1-x2)**2+(y1-y2)**2)   # 物体1和物体2之间的距离
        distance13 = np.sqrt((x1-x3)**2+(y1-y3)**2)   # 物体1和物体3之间的距离
        distance23 = np.sqrt((x2-x3)**2+(y2-y3)**2)   # 物体2和物体3之间的距离

        # 对物体1的计算
        a1_2 = G*m2/(distance12**2)  # 物体2对物体1的加速度（用上万有引力公式）
        a1_3 = G*m3/(distance13**2)  # 物体3对物体1的加速度
        a1_x = a1_2*(x2-x1)/distance12 + a1_3*(x3-x1)/distance13  # 物体1受到的水平加速度
        a1_y = a1_2*(y2-y1)/distance12 + a1_3*(y3-y1)/distance13  # 物体1受到的垂直加速度
        v1_x = v1_x + a1_x*t  # 物体1的速度
        v1_y = v1_y + a1_y*t  # 物体1的速度
        x1 = x1 + v1_x*t  # 物体1的水平位置
        y1 = y1 + v1_y*t  # 物体1的垂直位置
        x1_all = np.append(x1_all, x1)  # 记录轨迹
        y1_all = np.append(y1_all, y1)  # 记录轨迹

        # 对物体2的计算
        a2_1 = G*m1/(distance12**2)
        a2_3 = G*m3/(distance23**2)
        a2_x = a2_1*(x1-x2)/distance12 + a2_3*(x3-x2)/distance23
        a2_y = a2_1*(y1-y2)/distance12 + a2_3*(y3-y2)/distance23
        v2_x = v2_x + a2_x*t
        v2_y = v2_y + a2_y*t
        x2 = x2 + v2_x*t
        y2 = y2 + v2_y*t
        x2_all = np.append(x2_all, x2)
        y2_all = np.append(y2_all, y2)

        # 对物体3的计算
        a3_1 = G*m1/(distance13**2)
        a3_2 = G*m2/(distance23**2)
        a3_x = a3_1*(x1-x3)/distance13 + a3_2*(x2-x3)/distance23
        a3_y = a3_1*(y1-y3)/distance13 + a3_2*(y2-y3)/distance23
        v3_x = v3_x + a3_x*t
        v3_y = v3_y + a3_y*t
        x3 = x3 + v3_x*t
        y3 = y3 + v3_y*t
        x3_all = np.append(x3_all, x3)
        y3_all = np.append(y3_all, y3)

    # 选择观测坐标
    if True:
        axis_x = np.mean([x1, x2, x3])  # 观测坐标中心固定在平均值的地方
        axis_y = np.mean([y1, y2, y3])  # 观测坐标中心固定在平均值的地方
        while True:
            if np.abs(x1-axis_x) > observation_max or np.abs(x2-axis_x) > observation_max or np.abs(x3-axis_x) > observation_max or\
                    np.abs(y1-axis_y) > observation_max or np.abs(y2-axis_y) > observation_max or np.abs(y3-axis_y) > observation_max:
                observation_max = observation_max * 2  # 有一个物体超出视线时，视线范围翻倍
            elif np.abs(x1-axis_x) < observation_max/10 and np.abs(x2-axis_x) < observation_max/10 and np.abs(x3-axis_x) < observation_max/10 and\
                    np.abs(y1-axis_y) < observation_max/10 and np.abs(y2-axis_y) < observation_max/10 and np.abs(y3-axis_y) < observation_max/10:
                observation_max = observation_max / 2   # 所有物体都在的视线的10分之一内，视线范围减半
            else:
                break

    plt.axis([axis_x-observation_max, axis_x+observation_max,
             axis_y-observation_max,  axis_y+observation_max])

    # 默认密度相同，质量越大的，球面积越大。视线范围越宽，球看起来越小。
    if draw:
        plt.plot(x1, y1, 'og', markersize=m1*100/observation_max)
        plt.plot(x2, y2, 'or', markersize=m2*100/observation_max)
        plt.plot(x3, y3, 'ob', markersize=m3*100/observation_max)
        plt.plot(x1_all, y1_all, '-g')  # 画轨迹
        plt.plot(x2_all, y2_all, '-r')
        plt.plot(x3_all, y3_all, '-b')
        #print(str(x1_all),y1_all,x2_all,y2_all,x3_all,y3_all)
        #break
    
        
    
        plt.show()  # 显示图像
        plt.pause(0.00001)  # 暂停0.00001，防止画图过快

    if np.mod(i, save_r) == save_r-1:  # 当运动明显时，把图画出来
        i0 += 1
        time_now = time.time()
        print(f"第{i0}轮  总用时{time_now-start_time:.2f}s  此轮用时{time_now-time1:.2f}s  预计还有{(ranges-i)*(time_now-start_time)/(i+1):.2f}s")
        #string = (f"{i}\n\tx1:{x1:.12f},y1:{y1:.12f},v1_x:{v1_x:.12f},v1_y:{v1_y:.12f}\n" +
        #          f"\tx2:{x2:.12f},y2:{y2:.12f},v2_x:{v2_x:.12f},v2_y:{v2_y:.12f}\n" +
        #          f"\tx3:{x3:.12f},y3:{y3:.12f},v3_x:{v3_x:.12f},v3_y:{v3_y:.12f}\n")
        #print(string)
        #lt = time.localtime()
        #now_date_time = f"{lt.tm_year}-{lt.tm_mon}-{lt.tm_mday} {lt.tm_hour},{lt.tm_min},{lt.tm_sec}"
        with open(str(i0)+'.txt', "w", encoding="UTF-8") as file:
            #file.write((f"{i}    x1:{x1:.12f},y1:{y1:.12f},v1_x:{v1_x:.12f},v1_y:{v1_y:.12f}\t" +
            #            f"x2:{x2:.12f},y2:{y2:.12f},v2_x:{v2_x:.12f},v2_y:{v2_y:.12f}\t" +
            #            f"x3:{x3:.12f},y3:{y3:.12f},v3_x:{v3_x:.12f},v3_y:{v3_y:.12f}\n"))
            file.write(str(list(x1_all))+'\n')
            file.write(str(list(y1_all))+'\n')
            file.write(str(list(x2_all))+'\n')
            file.write(str(list(y2_all))+'\n')
            file.write(str(list(x3_all))+'\n')
            file.write(str(list(y3_all))+'\n')
            file.write(str(axis_x)+'\n'+str(axis_y)+'\n'+str(observation_max))
            x1_all = []
            y1_all = []
            x2_all = []
            y2_all = []
            x3_all = []
            y3_all = []
        time1 = time_now
        if draw:
            plt.show()  # 显示图像
            plt.pause(0.00001)  # 暂停0.00001，防止画图过快
            plt.savefig(str((i+1)/save_r)+'.jpg')  # 保存为图片可以用来做动画
            plt.clf()   # 清空

```

生图程序：
```python



import matplotlib.pyplot as plt
import os



os.chdir('E:/three-body/data')  # 设置路径

plt.ion()  # 开启交互模式
observation_max = 100  # 视线范围初始值
x1_all = []  # 轨迹初始值
y1_all = []
x2_all = []
y2_all = []
x3_all = []
y3_all = []

with open("log.txt", "r", encoding="UTF-8") as file:
    m1 = eval(file.readline())
    m2 = eval(file.readline())
    m3 = eval(file.readline())

all_length=0
for i in range(1,201):
    print(i,end='')
    with open(str(i)+".txt", "r", encoding="UTF-8") as file:
        x1 = eval(file.readline())
        y1 = eval(file.readline())
        x2 = eval(file.readline())
        y2 = eval(file.readline())
        x3 = eval(file.readline())
        y3 = eval(file.readline())
        axis_x = eval(file.readline())
        axis_y = eval(file.readline())
        observation_max = eval(file.readline())


    xys = x1, y1, x2, y2, x3, y3
    i0 = 1
    while(i0 < len(x1)):
        flag = 0
        for xy in xys:
            if(abs(xy[i0]-xy[i0-1]) < 1e-1):
                flag += 1
        if(flag==6):
            del x1[i0], x2[i0], x3[i0], y1[i0], y2[i0], y3[i0],
            i0 -= 1
        i0 += 1
    all_length += len(x1)
    print("  length:", all_length)
    x1_all += x1
    y1_all += y1
    x2_all += x2
    y2_all += y2
    x3_all += x3
    y3_all += y3

    plt.axis([axis_x-observation_max, axis_x+observation_max,
             axis_y-observation_max,  axis_y+observation_max])

    # 默认密度相同，质量越大的，球面积越大。视线范围越宽，球看起来越小。
    plt.plot(x1, y1, 'og', markersize=m1*100/observation_max)
    plt.plot(x2, y2, 'or', markersize=m2*100/observation_max)
    plt.plot(x3, y3, 'ob', markersize=m3*100/observation_max)
    plt.plot(x1_all, y1_all, '-g')  # 画轨迹
    plt.plot(x2_all, y2_all, '-r')
    plt.plot(x3_all, y3_all, '-b')
    plt.show()  # 显示图像
    plt.pause(0.001)  # 暂停0.00001，防止画图过快
    plt.savefig(str(i)+'.jpg')  # 保存为图片可以用来做动画
    plt.clf()   # 清空

```

guanjihuan说道：

2024年10月5日 00:44

感谢提供修改的代码供参考。

回复

匿名说道：

2023年9月19日 22:53

最后发现有的星星脱离了，是什么原因

回复
1. guanjihuan说道：
  
  2023年9月19日 23:13
  
  有两个可能的原因：（1）可能解就是这样的，由于速度比较大，且方向相反，会导致距离越来越远，引力越来越小。（2）也可能是计算错误。越往后面计算，误差越大，可能是误差积累导致的结果偏离真实情况。
  
  回复

修改了部分代码，增加了几个取值，去除了保存图片，改为动态显示，以及调整了几个参数让整个系统可以动态运行，目前还没统计运行了多久，反正很久，感兴趣的可以运行看看


import numpy as np
import matplotlib.pyplot as plt
import os

# 万有引力常数
G = 0.5

# 三体的质量
m1 = 7 # 绿色
m2 = 15 # 红
m3 = 8  # 蓝色

# 三体的初始位置
x1 = 100  # 绿色
y1 = 0

x2 = 0  # 红色
y2 = 0

x3 = 150  # 蓝色
y3 = 0

# 三体的初始速度
v1_x = -0.1  # 绿色
v1_y = -0.3
v2_x = 0  # 红色
v2_y = 0
v3_x = 0 # 蓝色
v3_y = 0.3

# 步长
t = 3

plt.ion()  # 开启交互模式
observation_max = 100  # 视线范围初始值
x1_all = [x1]  # 轨迹初始值
y1_all = [y1]
x2_all = [x2]
y2_all = [y2]
x3_all = [x3]
y3_all = [y3]

i = 0
for i in range(1000000):  
    distance12 = np.sqrt((x1-x2)**2+(y1-y2)**2)   # 物体1和物体2之间的距离
    distance13 = np.sqrt((x1-x3)**2+(y1-y3)**2)   # 物体1和物体3之间的距离
    distance23 = np.sqrt((x2-x3)**2+(y2-y3)**2)   # 物体2和物体3之间的距离
    old_x1 = x1
    old_x2 = x2
    old_x3 = x3
    old_y1 = y1
    old_y2 = y2
    old_y3 = y3
    # 对物体1的计算
    a1_2 = G*m2/(distance12**2)  # 物体2对物体1的加速度（用上万有引力公式）
    a1_3 = G*m3/(distance13**2)  # 物体3对物体1的加速度
    a1_x = a1_2*(old_x2-x1)/distance12 + a1_3*(old_x3-x1)/distance13  # 物体1受到的水平加速度
    a1_y = a1_2*(old_y2-y1)/distance12 + a1_3*(old_y3-y1)/distance13  # 物体1受到的垂直加速度
    v1_x = v1_x + a1_x*t  # 物体1的速度
    v1_y = v1_y + a1_y*t  # 物体1的速度
    x1 = x1 + v1_x*t  # 物体1的水平位置
    y1 = y1 + v1_y*t  # 物体1的垂直位置
    x1_all = np.append(x1_all, x1)  # 记录轨迹
    y1_all = np.append(y1_all, y1)  # 记录轨迹
    
    # 对物体2的计算
    a2_1 = G*m1/(distance12**2)
    a2_3 = G*m3/(distance23**2)
    a2_x = a2_1*(old_x1-x2)/distance12 + a2_3*(old_x3-x2)/distance23
    a2_y = a2_1*(old_y1-y2)/distance12 + a2_3*(old_y3-y2)/distance23
    v2_x = v2_x + a2_x*t
    v2_y = v2_y + a2_y*t
    x2 = x2 + v2_x*t
    y2 = y2 + v2_y*t
    x2_all = np.append(x2_all, x2)
    y2_all = np.append(y2_all, y2)
    
    # 对物体3的计算
    a3_1 = G*m1/(distance13**2)
    a3_2 = G*m2/(distance23**2)
    a3_x = a3_1*(old_x1-x3)/distance13 + a3_2*(old_x2-x3)/distance23
    a3_y = a3_1*(old_y1-y3)/distance13 + a3_2*(old_y2-y3)/distance23
    v3_x = v3_x + a3_x*t
    v3_y = v3_y + a3_y*t
    x3 = x3 + v3_x*t
    y3 = y3 + v3_y*t
    x3_all = np.append(x3_all, x3)
    y3_all = np.append(y3_all, y3)

    # 选择观测坐标
    axis_x = np.mean([x1, x2, x3])  # 观测坐标中心固定在平均值的地方
    axis_y = np.mean([y1, y2, y3])  # 观测坐标中心固定在平均值的地方
    while True:
        if np.abs(x1-axis_x) > observation_max or np.abs(x2-axis_x) > observation_max or np.abs(x3-axis_x) > observation_max or\
        np.abs(y1-axis_y) > observation_max or np.abs(y2-axis_y) > observation_max or np.abs(y3-axis_y) > observation_max:
            observation_max = observation_max * 2  # 有一个物体超出视线时，视线范围翻倍
        elif np.abs(x1-axis_x) < observation_max/10 and np.abs(x2-axis_x) < observation_max/10 and np.abs(x3-axis_x) < observation_max/10 and\
        np.abs(y1-axis_y) < observation_max/10 and np.abs(y2-axis_y) < observation_max/10 and np.abs(y3-axis_y) < observation_max/10:
            observation_max = observation_max / 2   # 所有物体都在的视线的10分之一内，视线范围减半
        else:
            break

    plt.axis([axis_x-observation_max, axis_x+observation_max, axis_y-observation_max,  axis_y+observation_max])
    
    plt.plot(x1, y1, 'og', markersize=m1*100/observation_max)  # 默认密度相同，质量越大的，球面积越大。视线范围越宽，球看起来越小。
    plt.plot(x2, y2, 'or', markersize=m2*100/observation_max) 
    plt.plot(x3, y3, 'ob', markersize=m3*100/observation_max)
    plt.plot(x1_all, y1_all, '-g')  # 画轨迹的
    plt.plot(x2_all, y2_all, '-r')
    plt.plot(x3_all, y3_all, '-b')

    if len(x2_all)==1000 or len(y2_all)==1000:
        x1_all = np.delete(x1_all, [0]) #清除旧尾迹
        x2_all = np.delete(x2_all, [0])
        x3_all = np.delete(x3_all, [0])
        y1_all = np.delete(y1_all, [0])
        y2_all = np.delete(y2_all, [0])
        y3_all = np.delete(y3_all, [0])
        if len(plt.get_fignums())==0:
            break

    plt.pause(0.001)  # 暂停0.00001，防止画图过快
    if len(plt.get_fignums())==0:
        break

    plt.clf()   # 清空

匿名说道：

2023年3月19日 10:15

“import numpy as np
import matplotlib.pyplot as plt
import os”
为何无法解析？

回复
1. guanjihuan说道：
  
  2023年3月21日 00:50
  
  是需要安装好包吧？参考：安装Python环境。
  
  回复

生成图片的速度很慢，是我电脑的问题吗，1分钟4张图片

匿名说道：

2023年2月14日 16:08

知足吧，我4分钟一张图片。

回复
1. 匿名说道：
  
  2023年2月15日 11:24
  
  我搞定了，去掉了生成图片的代码，让他实时显示出来
  
  回复

嗯，Python效率不高，可以试着对Python程序做优化。如果需要大量计算，建议用C语言或Fortran语言重写下程序。

我优化了你取值出现的小瑕疵，你可以加进去试试看


    distance12 = np.sqrt((x1-x2)**2+(y1-y2)**2)   # 物体1和物体2之间的距离
    distance13 = np.sqrt((x1-x3)**2+(y1-y3)**2)   # 物体1和物体3之间的距离
    distance23 = np.sqrt((x2-x3)**2+(y2-y3)**2)   # 物体2和物体3之间的距离
    old_x1 = x1
    old_x2 = x2
    old_x3 = x3
    old_y1 = y1
    old_y2 = y2
    old_y3 = y3
    # 对物体1的计算
    a1_2 = G*m2/(distance12**2)  # 物体2对物体1的加速度（用上万有引力公式）
    a1_3 = G*m3/(distance13**2)  # 物体3对物体1的加速度
    a1_x = a1_2*(old_x2-x1)/distance12 + a1_3*(old_x3-x1)/distance13  # 物体1受到的水平加速度
    a1_y = a1_2*(old_y2-y1)/distance12 + a1_3*(old_y3-y1)/distance13  # 物体1受到的垂直加速度
    v1_x = v1_x + a1_x*t  # 物体1的速度
    v1_y = v1_y + a1_y*t  # 物体1的速度
    x1 = x1 + v1_x*t  # 物体1的水平位置
    y1 = y1 + v1_y*t  # 物体1的垂直位置
    x1_all = np.append(x1_all, x1)  # 记录轨迹
    y1_all = np.append(y1_all, y1)  # 记录轨迹
    
    # 对物体2的计算
    a2_1 = G*m1/(distance12**2)
    a2_3 = G*m3/(distance23**2)
    a2_x = a2_1*(old_x1-x2)/distance12 + a2_3*(old_x3-x2)/distance23
    a2_y = a2_1*(old_y1-y2)/distance12 + a2_3*(old_y3-y2)/distance23
    v2_x = v2_x + a2_x*t
    v2_y = v2_y + a2_y*t
    x2 = x2 + v2_x*t
    y2 = y2 + v2_y*t
    x2_all = np.append(x2_all, x2)
    y2_all = np.append(y2_all, y2)
    
    # 对物体3的计算
    a3_1 = G*m1/(distance13**2)
    a3_2 = G*m2/(distance23**2)
    a3_x = a3_1*(old_x1-x3)/distance13 + a3_2*(old_x2-x3)/distance23
    a3_y = a3_1*(old_y1-y3)/distance13 + a3_2*(old_y2-y3)/distance23
    v3_x = v3_x + a3_x*t
    v3_y = v3_y + a3_y*t
    x3 = x3 + v3_x*t
    y3 = y3 + v3_y*t
    x3_all = np.append(x3_all, x3)
    y3_all = np.append(y3_all, y3)

Tak说道：

2023年2月15日 12:42
然后去掉整个输出图片的循环
加上
```
    if len(plt.get_fignums())==0:
        break
```
以及改plt.pause(0.001)
这样子就可以实时显示
回复


import numpy as np
import matplotlib.pyplot as plt
import os

# 万有引力常数
G = 0.5

# 三体的质量
m1 = 7 # 绿色
m2 = 15 # 红
m3 = 8  # 蓝色

# 三体的初始位置
x1 = 100  # 绿色
y1 = 0

x2 = 0  # 红色
y2 = 0

x3 = 150  # 蓝色
y3 = 0

# 三体的初始速度
v1_x = -0.1  # 绿色
v1_y = -0.3
v2_x = 0  # 红色
v2_y = 0
v3_x = 0 # 蓝色
v3_y = 0.3

# 步长
t = 3

plt.ion()  # 开启交互模式
observation_max = 100  # 视线范围初始值
x1_all = [x1]  # 轨迹初始值
y1_all = [y1]
x2_all = [x2]
y2_all = [y2]
x3_all = [x3]
y3_all = [y3]

i = 0
for i in range(1000000):  
    distance12 = np.sqrt((x1-x2)**2+(y1-y2)**2)   # 物体1和物体2之间的距离
    distance13 = np.sqrt((x1-x3)**2+(y1-y3)**2)   # 物体1和物体3之间的距离
    distance23 = np.sqrt((x2-x3)**2+(y2-y3)**2)   # 物体2和物体3之间的距离
    old_x1 = x1
    old_x2 = x2
    old_x3 = x3
    old_y1 = y1
    old_y2 = y2
    old_y3 = y3
    # 对物体1的计算
    a1_2 = G*m2/(distance12**2)  # 物体2对物体1的加速度（用上万有引力公式）
    a1_3 = G*m3/(distance13**2)  # 物体3对物体1的加速度
    a1_x = a1_2*(old_x2-x1)/distance12 + a1_3*(old_x3-x1)/distance13  # 物体1受到的水平加速度
    a1_y = a1_2*(old_y2-y1)/distance12 + a1_3*(old_y3-y1)/distance13  # 物体1受到的垂直加速度
    v1_x = v1_x + a1_x*t  # 物体1的速度
    v1_y = v1_y + a1_y*t  # 物体1的速度
    x1 = x1 + v1_x*t  # 物体1的水平位置
    y1 = y1 + v1_y*t  # 物体1的垂直位置
    x1_all = np.append(x1_all, x1)  # 记录轨迹
    y1_all = np.append(y1_all, y1)  # 记录轨迹
    
    # 对物体2的计算
    a2_1 = G*m1/(distance12**2)
    a2_3 = G*m3/(distance23**2)
    a2_x = a2_1*(old_x1-x2)/distance12 + a2_3*(old_x3-x2)/distance23
    a2_y = a2_1*(old_y1-y2)/distance12 + a2_3*(old_y3-y2)/distance23
    v2_x = v2_x + a2_x*t
    v2_y = v2_y + a2_y*t
    x2 = x2 + v2_x*t
    y2 = y2 + v2_y*t
    x2_all = np.append(x2_all, x2)
    y2_all = np.append(y2_all, y2)
    
    # 对物体3的计算
    a3_1 = G*m1/(distance13**2)
    a3_2 = G*m2/(distance23**2)
    a3_x = a3_1*(old_x1-x3)/distance13 + a3_2*(old_x2-x3)/distance23
    a3_y = a3_1*(old_y1-y3)/distance13 + a3_2*(old_y2-y3)/distance23
    v3_x = v3_x + a3_x*t
    v3_y = v3_y + a3_y*t
    x3 = x3 + v3_x*t
    y3 = y3 + v3_y*t
    x3_all = np.append(x3_all, x3)
    y3_all = np.append(y3_all, y3)

    # 选择观测坐标
    axis_x = np.mean([x1, x2, x3])  # 观测坐标中心固定在平均值的地方
    axis_y = np.mean([y1, y2, y3])  # 观测坐标中心固定在平均值的地方
    while True:
        if np.abs(x1-axis_x) > observation_max or np.abs(x2-axis_x) > observation_max or np.abs(x3-axis_x) > observation_max or\
        np.abs(y1-axis_y) > observation_max or np.abs(y2-axis_y) > observation_max or np.abs(y3-axis_y) > observation_max:
            observation_max = observation_max * 2  # 有一个物体超出视线时，视线范围翻倍
        elif np.abs(x1-axis_x) < observation_max/10 and np.abs(x2-axis_x) < observation_max/10 and np.abs(x3-axis_x) < observation_max/10 and\
        np.abs(y1-axis_y) < observation_max/10 and np.abs(y2-axis_y) < observation_max/10 and np.abs(y3-axis_y) < observation_max/10:
            observation_max = observation_max / 2   # 所有物体都在的视线的10分之一内，视线范围减半
        else:
            break

    plt.axis([axis_x-observation_max, axis_x+observation_max, axis_y-observation_max,  axis_y+observation_max])
    
    plt.plot(x1, y1, 'og', markersize=m1*100/observation_max)  # 默认密度相同，质量越大的，球面积越大。视线范围越宽，球看起来越小。
    plt.plot(x2, y2, 'or', markersize=m2*100/observation_max) 
    plt.plot(x3, y3, 'ob', markersize=m3*100/observation_max)
    plt.plot(x1_all, y1_all, '-g')  # 画轨迹的
    plt.plot(x2_all, y2_all, '-r')
    plt.plot(x3_all, y3_all, '-b')

    if len(x2_all)==1000 or len(y2_all)==1000:
        x1_all = np.delete(x1_all, [0]) #清除旧尾迹
        x2_all = np.delete(x2_all, [0])
        x3_all = np.delete(x3_all, [0])
        y1_all = np.delete(y1_all, [0])
        y2_all = np.delete(y2_all, [0])
        y3_all = np.delete(y3_all, [0])
        if len(plt.get_fignums())==0:
            break

    plt.pause(0.001)  # 暂停0.00001，防止画图过快
    if len(plt.get_fignums())==0:
        break

    plt.clf()   # 清空

匿名说道：

2023年1月6日 20:52

我的程序运行了以后显示0,1,2,一个一个出数是什么情况

回复
1. guanjihuan说道：
  
  2023年1月8日 18:02
  
  可以看程序中的print代码，保存图片时打印的。这里可以代表当前保存文件的个数。
  
  回复
匿名说道：

2022年10月21日 16:26

非常棒！

回复
我是谁我在哪我在干什么说道：

2021年6月28日 09:08

我卡了是什么回事？

回复
1. guanjihuan说道：
  
  2021年6月28日 13:21
  
  哪里卡了
  
  回复
  1. 匿名说道：
    
    2023年1月17日 11:17
    
    我也是一样的问题，一运行就卡住，窗口无响应，只有控制台打印数字，图像看不到
    
    回复
    1. guanjihuan说道：
      
      2023年1月17日 11:32
      
      图像保存为图片文件了，可以在代码文件所在的文件夹找找。或者设置下路径，再重新运行。
      
      回复
      1. 匿名说道：
        
        2023年1月17日 14:20
        
        这样啊，就是卡才是正常的，把生成的图片制作的GIF动画才是最终的结果，我以为是实时预览的
        
        回复
        
        guanjihuan说道：
        
        2023年1月17日 18:35
        
        嗯，不是实时预览的。因为一次的计算时长比较长，所以直接保存为JPG图片或GIF动画文件会更好些。其实更好的数据保存格式应该是文本格式，保存所有计算结果的坐标。
        
        回复
匿名说道：

2020年11月22日 15:30

您好，请问(x2-x1)/distance12怎么来的呢？
距离的平方的比才是加速度的比值吧？

回复
1. guanjihuan说道：
  
  2020年11月22日 15:47
  
  这个不是加速度，是cos，是为了得到水平方向移动的分量。
  
  回复
  1. 匿名说道：
    
    2020年11月22日 16:09
    
    谢谢！是我理解错了~
    
    回复
狄拉克的符号说道：

2020年5月12日 12:23

万有引力不应该是平方反比的吗？为啥作者计算加速度的时候distance没有平方呢？

回复
1. guanjihuan说道：
  
  2020年5月13日 01:56
  
  抱歉，我公式搞混了，谢谢提醒。已经修改成距离的平方了。
  
  回复
2. 匿名说道：
  
  2023年1月6日 20:49
  
  distance**2就是平方的意思
  
  回复
  1. guanjihuan说道：
    
    2023年1月8日 18:07
    
    嗯，我之前漏写平方了，当前版本是已经修改后的
    
    回复

1. 三体的质量相差不大的情况

2. 考虑其中有一个球相对较大的情况

3. 某个球修改为大质量，模拟恒星-行星系统

Published by guanjihuan

32 thoughts on “在二维平面模拟三体运动（附Python代码）”

发表评论 取消回复

发表评论取消回复