使用蒙特卡洛计算定积分（附Python代码）

网上有很多介绍蒙特卡洛计算定积分。因为这是蒙特卡洛方法的经典案例，所以我这里也摘抄整理下。

一般来说，数值计算定积分是将面积细分为小矩阵，然后求和，细分越多越精确。这篇是采用蒙特卡洛的方法来计算定积分，有投点法、期望法（或称作平均值法）两种。期望法会更重要些。

1. 蒙特卡洛求定积分：投点法

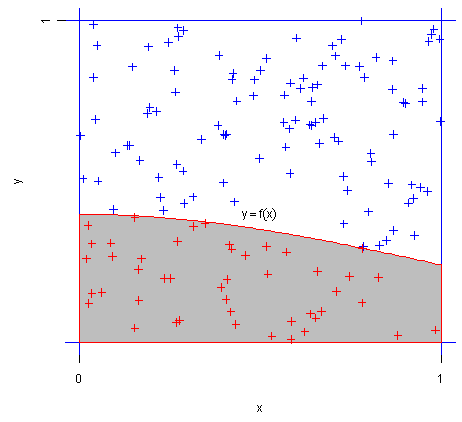
这个很好理解。红点占所有点的比例，乘方形面积，就是函数 $f(x)$ 的积分值。

2. 蒙特卡洛求定积分：期望法

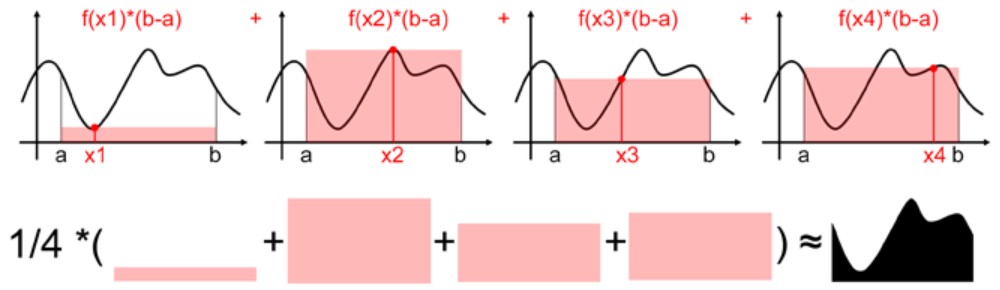
直观的图像如上所示，采样后求平均。写成求和公式：

$\begin{equation*} \bar{E}=(b-a)\frac{1}{N}\sum_{i=1}^{N}f(X_{i}) \end{equation*}$

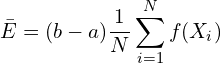
原理来自于“强大数定理”，可证明得到以下公式：

$\begin{equation*} Pr(\lim\limits_{N\rightarrow\infty}\frac{1}{N}\sum_{i=1}^{N}g(X_{i})=\int_{a}^{b}f(x)dx )=1 \end{equation*}$

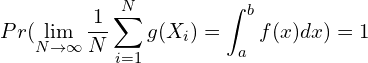
其中， $g(X_{i})=\frac{f(X_{i})}{p(X_{i})}$ ， $p(x)$ 是概率密度函数pdf (probability density function)。也就是说在 $p(x)$ 的分布下，抽取 $x$ 样本，当 $N$ 足够大时，可以采用均值来近似 $f(x)$ 的积分：

$\begin{equation*} \int _{a}^{b}{f(x)dx} \approx \frac{g(x_1) + g(x_2) + ... + g(x_N)}{N} \end{equation*}$

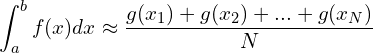
以上图片的例子是选取了均匀分布函数 $p(x)=\frac{1}{b-a}$ 的情况。

一般来说均匀分布计算的效率不会高，需要另外选取一个合理的分布提高计算效率，例如高斯函数在峰值附近积分贡献比较多，应该赋予更多的采样。这个技术叫做“重要性采样” (importance sampling)。均匀分布、高斯分布、Gamma分布等都属于简单分布采样（或者概率分布采样）。

如果是采用比较复杂的分布 $p(X_{i})$ ，即使已知该分布，很难直接获取符合该分布的样本 $\{x_{1}, x_{2}, ..., x_{N}\}$ ，这时候需要使用“接受-拒绝采样”、 “马尔科夫链-蒙特卡洛 (MCMC) 采样”、“ Metropolis-Hastings (M-H)采样”、“Gibbs采样”等方法。

这篇的Python代码如下（以 $\int_{0}^{1}x^{2}dx$ 积分为例）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/1145
"""

import numpy as np
import random
import time


def integral():   # 直接数值积分
    integral_value = 0
    for x in np.arange(0, 1, 1/10**7):
        integral_value = integral_value + x**2*(1/10**7)   # 对x^2在0和1之间积分
    return integral_value


def MC_1():  # 蒙特卡洛求定积分1：投点法
    n = 10**7
    x_min, x_max = 0.0, 1.0
    y_min, y_max = 0.0, 1.0
    count = 0
    for i in range(0, n):
        x = random.uniform(x_min, x_max)
        y = random.uniform(y_min, y_max)
        # x*x > y，表示该点位于曲线的下面。所求的积分值即为曲线下方的面积与正方形面积的比。
        if x * x > y:
            count += 1
    integral_value = count / n
    return integral_value


def MC_2():  # 蒙特卡洛求定积分2：期望法
    n = 10**7
    x_min, x_max = 0.0, 1.0
    integral_value = 0
    for i in range(n):
        x = random.uniform(x_min, x_max)
        integral_value = integral_value + (1-0)*x**2
    integral_value = integral_value/n
    return integral_value


print('【计算时间】')
start_clock = time.perf_counter()  # 或者用time.clock()
a00 = 1/3  # 理论值
end_clock = time.perf_counter()
print('理论值（解析）：', end_clock-start_clock)
start_clock = time.perf_counter()
a0 = integral()  # 直接数值积分
end_clock = time.perf_counter()
print('直接数值积分：', end_clock-start_clock)
start_clock = time.perf_counter()
a1 = MC_1()  # 用蒙特卡洛求积分投点法
end_clock = time.perf_counter()
print('用蒙特卡洛求积分_投点法：', end_clock-start_clock)
start_clock = time.perf_counter()
a2 = MC_2()
end_clock = time.perf_counter()
print('用蒙特卡洛求积分_期望法：', end_clock-start_clock, '\n')

print('【计算结果】')
print('理论值（解析）：', a00)
print('直接数值积分：', a0)
print('用蒙特卡洛求积分_投点法：', a1)
print('用蒙特卡洛求积分_期望法：', a2, '\n')

print('【计算误差】')
print('理论值（解析）：', 0)
print('直接数值积分：', abs(a0-1/3))
print('用蒙特卡洛求积分_投点法：', abs(a1-1/3))
print('用蒙特卡洛求积分_期望法：', abs(a2-1/3))

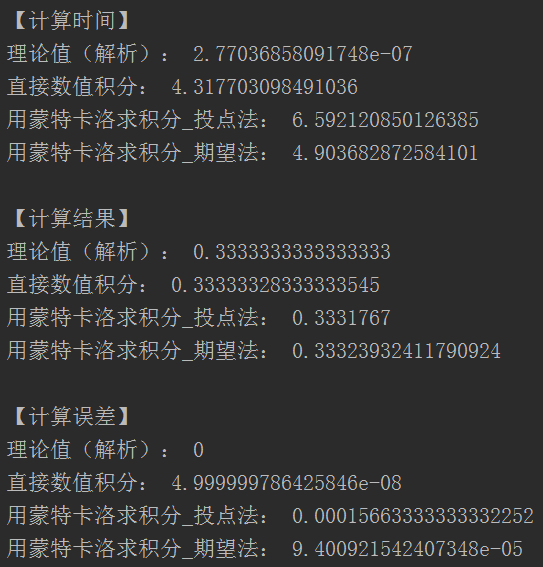
计算结果：