参考文献为:Di Xiao, Wang Yao, and Qian Niu, “Valley-Contrasting Physics in Graphene: Magnetic Moment and Topological Transport”, Phys. Rev. Lett. 99, 236809 (2007)。在文献中考虑的石墨烯模型是在狄拉克点附近的线性模型,而本篇考虑的石墨烯的紧束缚模型。
本篇采用的是贝里曲率的定义公式,其他的贝里曲率计算方法阅读这篇:贝里曲率的计算(附Python代码)。本篇的参考博文为:
石墨烯在倒空间的示意图:
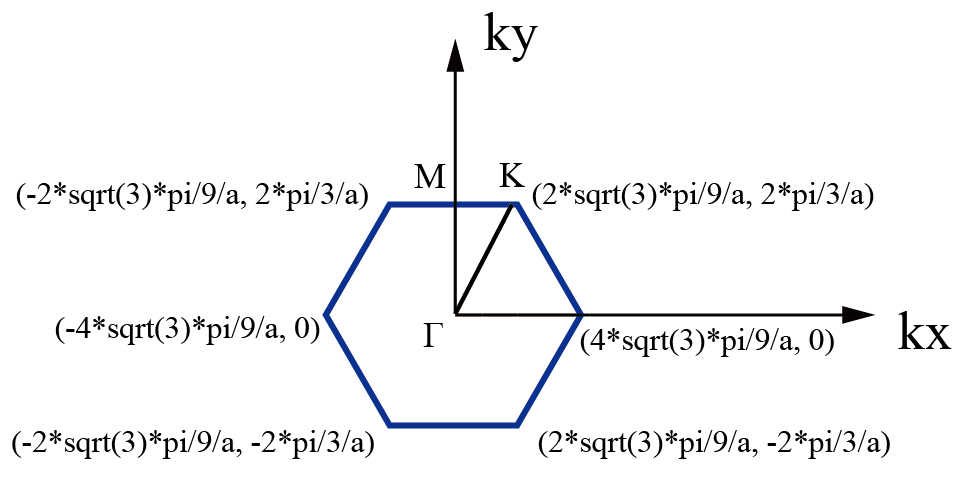
一、考虑k_y=0对称轴上的贝里曲率的分布
代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/8536
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import time
def hamiltonian(k1, k2, t1=2.82, a=1/sqrt(3)): # 石墨烯哈密顿量(a为原子间距,不赋值的话默认为1/sqrt(3))
h = np.zeros((2, 2), dtype=complex)
h[0, 0] = 0.28/2
h[1, 1] = -0.28/2
h[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h[0, 1] = h[1, 0].conj()
return h
def main():
start_time = time.time()
n = 2000 # 取点密度
delta = 1e-9 # 求导的偏离量
for band in range(2):
F_all = [] # 贝里曲率
for kx in np.linspace(-2*pi, 2*pi, n):
for ky in [0]: # 这里只考虑ky=0对称轴上的情况 # np.linspace(-pi, pi, n):
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 价带波函数
# print(np.argsort(np.real(eigenvalue))[0]) # 排序索引(从小到大)
# print(eigenvalue) # 排序前的本征值
# print(np.sort(np.real(eigenvalue))) # 排序后的本征值(从小到大)
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx的波函数
# vector_delta_kx = find_vector_with_the_same_gauge(vector_delta_kx, vector) # 如果波函数不连续需要使用这个
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离ky的波函数
# vector_delta_ky = find_vector_with_the_same_gauge(vector_delta_ky, vector) # 如果波函数不连续需要使用这个
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx和ky的波函数
# vector_delta_kx_ky = find_vector_with_the_same_gauge(vector_delta_kx_ky, vector) # 如果波函数不连续需要使用这个
# 价带的波函数的贝里联络(berry connection) # 求导后内积
A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta) # 贝里联络Ax(x分量)
A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta) # 贝里联络Ay(y分量)
A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta) # 略偏离ky的贝里联络Ax
A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta) # 略偏离kx的贝里联络Ay
# 贝里曲率(berry curvature)
F = ((A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta)*1j
# print(F)
F_all = np.append(F_all,[F], axis=0)
plt.plot(np.linspace(-2*pi, 2*pi, n)/pi, np.real(F_all))
plt.xlabel('k_x (pi)')
plt.ylabel('Berry curvature')
if band==0:
plt.title('Valence Band')
else:
plt.title('Conductance Band')
plt.show()
end_time = time.time()
print('运行时间(min)=', (end_time-start_time)/60)
def find_vector_with_the_same_gauge(vector_1, vector_0):
# 寻找近似的同一的规范
phase_1_pre = 0
phase_2_pre = pi
n_test = 10001
for i0 in range(n_test):
test_1 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_1_pre) - vector_0))
test_2 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_2_pre) - vector_0))
if test_1 < 1e-9:
phase = phase_1_pre
# print('Done with i0=', i0)
break
if i0 == n_test-1:
phase = phase_1_pre
print('Gauge Not Found with i0=', i0)
if test_1 < test_2:
if i0 == 0:
phase_1 = phase_1_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_1_pre
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
if i0 == 0:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre
phase_1_pre = phase_1
phase_2_pre = phase_2
vector_1 = vector_1*cmath.exp(1j*phase)
# print('二分查找找到的规范=', phase)
return vector_1
if __name__ == '__main__':
main()计算结果为:
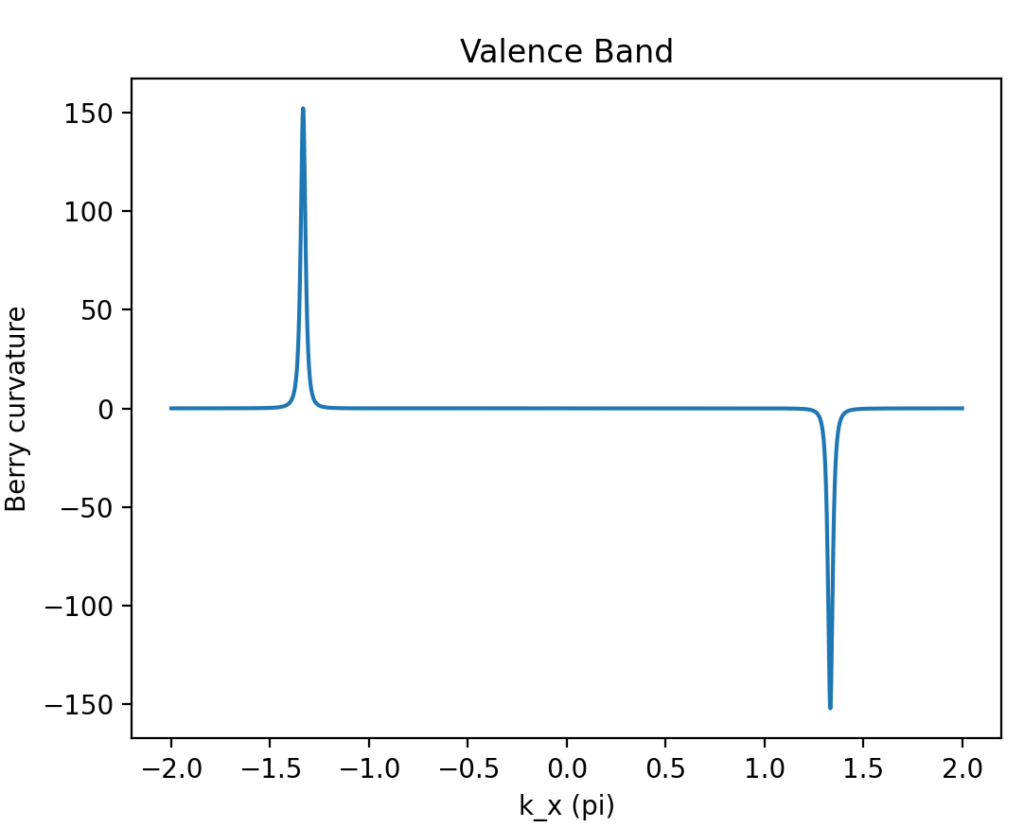
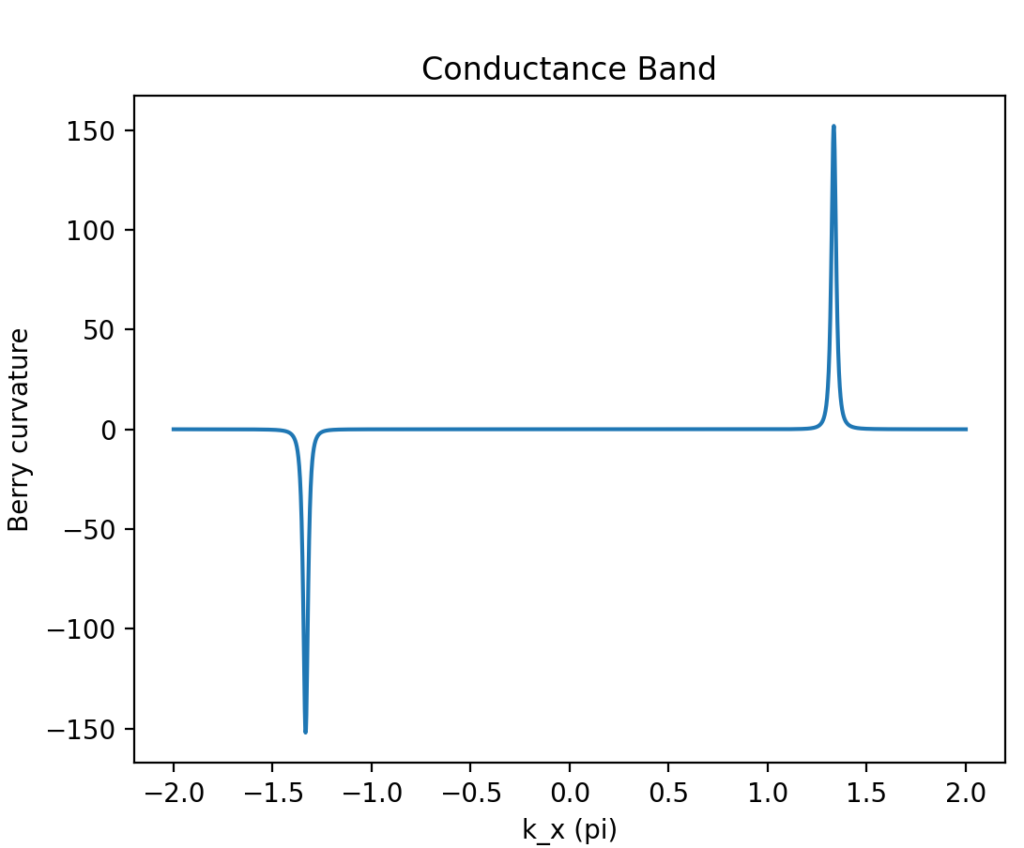
二、考虑二维k空间的贝里曲率分布
代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/8536
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import time
def hamiltonian(k1, k2, t1=2.82, a=1/sqrt(3)): # 石墨烯哈密顿量(a为原子间距,不赋值的话默认为1/sqrt(3))
h = np.zeros((2, 2), dtype=complex)
h[0, 0] = 0.28/2
h[1, 1] = -0.28/2
h[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
h[0, 1] = h[1, 0].conj()
return h
def main():
start_time = time.time()
n = 400 # 取点密度
delta = 1e-10 # 求导的偏离量
kx_array = np.linspace(-2*pi, 2*pi, n)
ky_array = np.linspace(-2*pi, 2*pi, n)
for band in range(2):
F_all = np.zeros((ky_array.shape[0], ky_array.shape[0])) # 贝里曲率
j0 = 0
for kx in kx_array:
print(kx)
i0 = 0
for ky in ky_array:
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 价带波函数
# print(np.argsort(np.real(eigenvalue))[0]) # 排序索引(从小到大)
# print(eigenvalue) # 排序前的本征值
# print(np.sort(np.real(eigenvalue))) # 排序后的本征值(从小到大)
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx的波函数
# vector_delta_kx = find_vector_with_the_same_gauge(vector_delta_kx, vector) # 如果波函数不连续需要使用这个
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离ky的波函数
# vector_delta_ky = find_vector_with_the_same_gauge(vector_delta_ky, vector) # 如果波函数不连续需要使用这个
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[band]] # 略偏离kx和ky的波函数
# vector_delta_kx_ky = find_vector_with_the_same_gauge(vector_delta_kx_ky, vector) # 如果波函数不连续需要使用这个
# 价带的波函数的贝里联络(berry connection) # 求导后内积
A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta) # 贝里联络Ax(x分量)
A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta) # 贝里联络Ay(y分量)
A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta) # 略偏离ky的贝里联络Ax
A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta) # 略偏离kx的贝里联络Ay
# 贝里曲率(berry curvature)
F = ((A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta)*1j
# print(F)
F_all[i0, j0] = np.real(F)
i0 += 1
j0 += 1
if band==0:
plot_3d_surface(kx_array/pi, ky_array/pi, F_all, xlabel='k_x (pi)', ylabel='k_y (pi)', zlabel='Berry curvature', title='Valence Band', rcount=300, ccount=300)
else:
plot_3d_surface(kx_array/pi, ky_array/pi, F_all, xlabel='k_x (pi)', ylabel='k_y (pi)', zlabel='Berry curvature', title='Conductance Band', rcount=300, ccount=300)
# import guan
# if band==0:
# guan.plot_3d_surface(kx_array/pi, ky_array/pi, F_all, xlabel='kx', ylabel='ky', zlabel='Berry curvature', title='Valence Band', rcount=300, ccount=300)
# else:
# guan.plot_3d_surface(kx_array/pi, ky_array/pi, F_all, xlabel='kx', ylabel='ky', zlabel='Berry curvature', title='Conductance Band', rcount=300, ccount=300)
end_time = time.time()
print('运行时间(min)=', (end_time-start_time)/60)
def find_vector_with_the_same_gauge(vector_1, vector_0):
# 寻找近似的同一的规范
phase_1_pre = 0
phase_2_pre = pi
n_test = 10001
for i0 in range(n_test):
test_1 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_1_pre) - vector_0))
test_2 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_2_pre) - vector_0))
if test_1 < 1e-9:
phase = phase_1_pre
# print('Done with i0=', i0)
break
if i0 == n_test-1:
phase = phase_1_pre
print('Gauge Not Found with i0=', i0)
if test_1 < test_2:
if i0 == 0:
phase_1 = phase_1_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_1_pre
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
if i0 == 0:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre
phase_1_pre = phase_1
phase_2_pre = phase_2
vector_1 = vector_1*cmath.exp(1j*phase)
# print('二分查找找到的规范=', phase)
return vector_1
def plot_3d_surface(x_array, y_array, matrix, xlabel='x', ylabel='y', zlabel='z', title='', fontsize=20, labelsize=15, show=1, save=0, filename='a', file_format='.jpg', dpi=300, z_min=None, z_max=None, rcount=100, ccount=100):
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
matrix = np.array(matrix)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
plt.subplots_adjust(bottom=0.1, right=0.65)
x_array, y_array = np.meshgrid(x_array, y_array)
if len(matrix.shape) == 2:
surf = ax.plot_surface(x_array, y_array, matrix, rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False)
elif len(matrix.shape) == 3:
for i0 in range(matrix.shape[2]):
surf = ax.plot_surface(x_array, y_array, matrix[:,:,i0], rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman')
ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman')
ax.set_zlabel(zlabel, fontsize=fontsize, fontfamily='Times New Roman')
ax.zaxis.set_major_locator(LinearLocator(5))
ax.zaxis.set_major_formatter('{x:.2f}')
if z_min!=None or z_max!=None:
if z_min==None:
z_min=matrix.min()
if z_max==None:
z_max=matrix.max()
ax.set_zlim(z_min, z_max)
ax.tick_params(labelsize=labelsize)
labels = ax.get_xticklabels() + ax.get_yticklabels() + ax.get_zticklabels()
[label.set_fontname('Times New Roman') for label in labels]
cax = plt.axes([0.8, 0.1, 0.05, 0.8])
cbar = fig.colorbar(surf, cax=cax)
cbar.ax.tick_params(labelsize=labelsize)
for l in cbar.ax.yaxis.get_ticklabels():
l.set_family('Times New Roman')
if save == 1:
plt.savefig(filename+file_format, dpi=dpi)
if show == 1:
plt.show()
plt.close('all')
if __name__ == '__main__':
main()计算结果为:
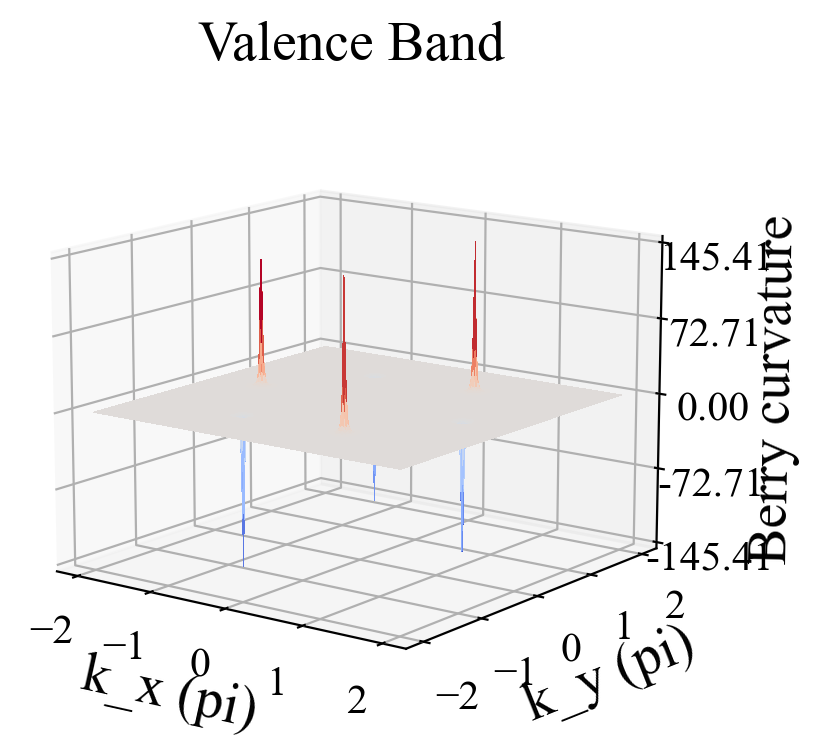
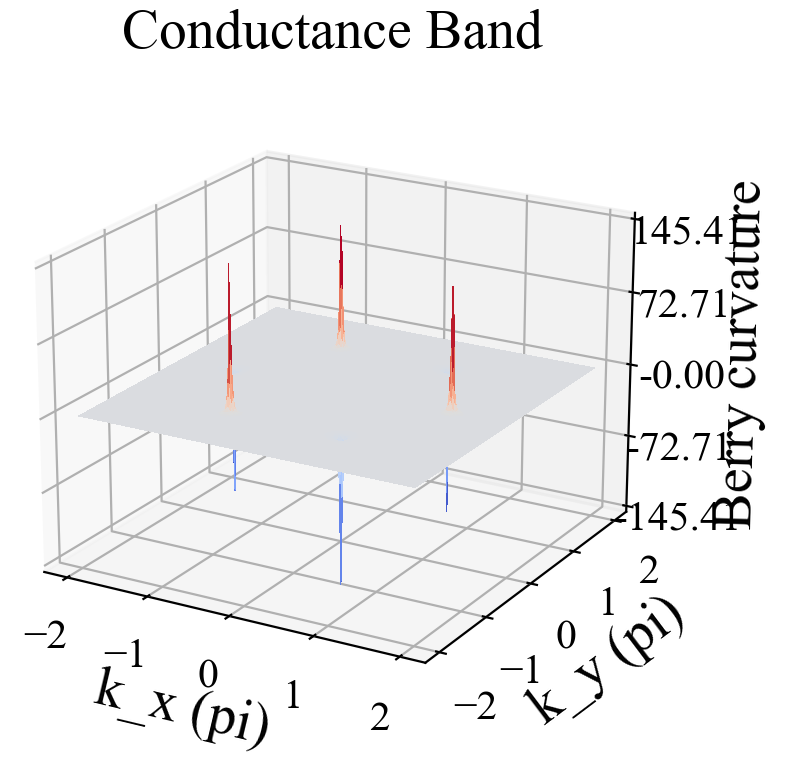
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
关老师您好,请问贝利曲率有单位吗,我看文献上单位都写的是Bohr^2,但是通过贝利曲率的公式感觉是对波函数的求导以及内积,没看出有单位是什么,您能帮忙解答一下吗
贝里曲率的单位确实是长度的平方,只是平时会比较少去提及。有两个角度可以理解:(1)陈数是没有单位的,陈数为贝里曲率对布里渊区的面积分,因为倒空间坐标的单位是长度的倒数,所以贝里曲率的单位就是长度的平方。需要注意的是:用上波尔长度的平方(Bohr^2),数值上是需要进行调整的。(2)不妨把波函数想象为平面波exp(ika),贝里联络中需要波函数对k求导,于是会出现一个长度单位;贝里曲率需要对贝里联络进行求导,还会跑出一个长度单位,所以贝里曲率的单位是长度的平方。
明白了,谢谢您解答
博主你好,我很好奇,Valley-Contrasting Physics in Graphene: Magnetic Moment and Topological Transport文章哈密顿量中的赝自旋系数是怎样作用在Hamilton
量上的。可以看出,数值计算的模型应该是一个加了质量想的石墨烯模型,并没有添加t_z项
嗯,就只是加了一个质量项。你说的t_z项是什么,石墨烯是一个二维的体系,没有z方向的跃迁。
博主您好,可不可以出个matlab版?非常感谢
暂时没有,语义差不多的,可以自己翻译过去。或者根据定义直接写。
好的谢谢
博主你好,我想问下,理论和计算凝聚态物理真的需要学python吗?是不是代码都是用python写的?
不是呀,其实凝聚态物理中很多代码都是用Fortran和Matlab写的,也有用C语言的。主要还是看写的内容,跟编程语言无关,想用哪个语言都可以。Fortran和C语言的运行效率会比较高一些。Python+NumPy和Matlab差不多的,Matlab是商业软件,Python是开源的。Python运行效率没有Fortran高,我主要是图书写方便不用定义变量,各种库比较多方便调用,又是开源的,而且最近因为机器学习Python语言也比较火,然后我就用了。