这是之前的两篇:二维电子气的朗道能级、狄拉克电子朗道能级的根号N分布。
本篇用粒子数算符求解朗道能级。
1. 二维电子气的朗道能级
以二维电子气为例,哈密顿量为:
![]()
参考之前的博文,在磁场下:
![]()
存在关系:
![]()
定义:
![]()
![]()
![]() 和
和![]() 满足对易关系:
满足对易关系:
![]()
![]() 为粒子数算符,展开写成:
为粒子数算符,展开写成:
![Rendered by QuickLaTeX.com \begin{aligned} a^{\dagger}a&=\frac{1}{2eB\hbar}[(p_x+eBy)-ip_y][(p_x+eBy)+ip_y]\\&=\frac{1}{2eB\hbar}[(p_x+eBy)^2+p_y^2-eB\hbar]\\&=\frac{1}{2eB\hbar}[(p_x+eBy)^2+p_y^2]-\frac{1}{2}\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-6b1126f76a4333c4f94fc341fa64957a_l3.png)
哈密顿量可以由![]() 来表示:
来表示:
![]()
其中,![]() 。于是,朗道能级为:
。于是,朗道能级为:![]()
2. 狄拉克费米子的朗道能级
狄拉克电子最小哈密顿量:
![]()
参考之前的博文,在磁场下:
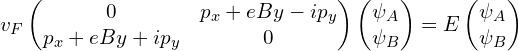
同上,定义:
![]()
![]()
于是有:
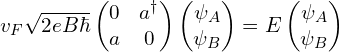
朗道能级:E=![]()
参考资料:
[1] 季燕江《量子力学讲义》的4.2节、6.5节、8.3节
[2] http://hitoshi.berkeley.edu/221a/landau.pdf
[3] http://web.physics.ucsb.edu/~phys123B/w2015/lecture5.pdf
[4] http://bingweb.binghamton.edu/~suzuki/QuantumMechanicsII/14-5_Landau_level.pdf
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】