学术, 量子输运

纵向/横向电阻率和纵向/横向电导率的关系

发布时间：2021年8月24日2022年7月14日

最近修改时间：2022年7月14日

电阻率（resistivity）张量[1]：

$\rho=\begin{pmatrix} \rho_{xx} & \rho _{xy} \\ - \rho_{xy} & \rho_{xx} \end{pmatrix}$

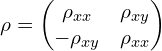
电导率（conductiviy）张量：

$\sigma=\begin{pmatrix} \sigma_{xx} & \sigma_{xy} \\ -\sigma_{xy} & \sigma_{xx} \end{pmatrix}$

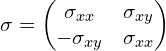
有用到关系式： $\sigma_{yx}=-\sigma_{xy}$ ， $\rho_{yx}=-\rho_{xy}$ 。其中， $\rho_{xx}$ 和 $\sigma_{xx}$ 分别为纵向电阻率和纵向电导率； $\rho_{xy}$ 和 $\sigma_{xy}$ 分别为横向（霍尔）电阻率和横向（霍尔）电导率。

两者关系： $\sigma \cdot \rho =1$ 。

展开后有：

$\left\{ \begin{aligned} & \sigma_{xx} \rho_{xx} - \sigma_{xy}\rho_{xy}=1 \\ & \sigma_{xx} \rho_{xy} + \sigma_{xy}\rho_{xx}=0 \end{aligned} \right.$

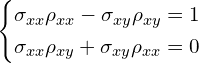
推导得到以下公式：

$\rho_{xx}=\frac{\sigma_{xx}}{\sigma_{xx}^2+\sigma_{xy}^2} \quad \quad \rho_{xy}=-\frac{\sigma_{xy}}{\sigma_{xx}^2+\sigma_{xy}^2}$

$\sigma_{xx}=\frac{\rho_{xx}}{\rho_{xx}^2+\rho_{xy}^2} \quad \quad \sigma_{xy}=-\frac{\rho_{xy}}{\rho_{xx}^2+\rho_{xy}^2}$

于是有结论[2]：

（1）当 $\rho_{xy}=0$ 时，有常见的关系式： $\sigma_{xx}=\frac{1}{\rho_{xx}}$ 。

（2）当 $\rho_{xy}\neq 0$ 时，如果 $\rho_{xx}=0$ ，那么 $\sigma_{xx}=0$ 。

参考资料：

[1] Supriyo Datta, Electronic transport in mesoscopic systems, 2004, P23-P26.

[2] https://www.zybuluo.com/zhouhuibin/note/858185

4,876 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

发表评论取消回复