原文
- Ji-Huan Guan, Yan-Yang Zhang*, Si-Si Wang, Yan Yu, Yang Xia and Shu-Shen Li, Barrier Tunneling and Loop Polarization in Hopf Semimetals. Phys. Rev. B 102, 064203 (2020).
通讯作者学术报告:节线半金属的量子输运性质以及圈极化现象 (koushare.com)。
评价:相对于谷电子学中的谷自由度,圈自由度的构型会更加丰富,而极化是利用某个自由度的重要前提。该工作的主要价值体现在维度上的一个推广,继承了电荷电子学、自旋电子学和谷电子学的概念,为电子学的发展提供了一种新的可能性。
摘要
拓扑半金属包括了节点半金属(即外尔/狄拉克半金属)和节线半金属。在节线半金属中,导带和价带相交于一条或多条一维的线,在三维的倒空间中具有更加丰富的几何或拓扑结构。对于多个节线圈的节线半金属,例如霍普夫半金属(Hopf semimetal),节线圈作为一个新的自由度,与电荷、自旋、谷电子类似,有望发展成为一种新型的电子器件或信息载体,即“圈电子学”(looptronics)。本文将介绍霍普夫半金属在势垒散射和无序散射过程中圈电子的极化现象,其中,无序散射中的圈极化现象可归因于向前或向后输运通道的非对称性。此外,我们提出了一种可能探测圈极化率的量子输运方案。
1. 霍普夫半金属模型
![]()
其中,
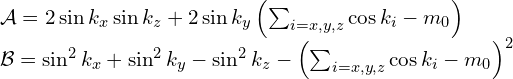
同时令![]() ,
,![]() ,求得两组零能解:
,求得两组零能解:
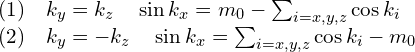
分别对应于蓝圈和红圈。当![]() 时,两个圈是相互嵌套的(linked);当
时,两个圈是相互嵌套的(linked);当![]() 时,两个圈是非相互嵌套的(unlinked)。
时,两个圈是非相互嵌套的(unlinked)。
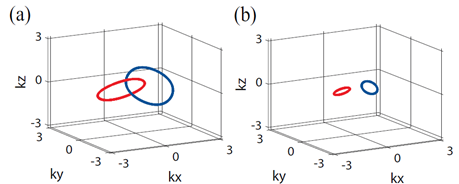
![]() 是相变点。当增加
是相变点。当增加![]() 时,在
时,在![]() 中间区域的局域能带发生反转,发生了倒空间中的几何拓扑相变,两个节线圈由相互嵌套转变成非相互嵌套,如下图所示。
中间区域的局域能带发生反转,发生了倒空间中的几何拓扑相变,两个节线圈由相互嵌套转变成非相互嵌套,如下图所示。
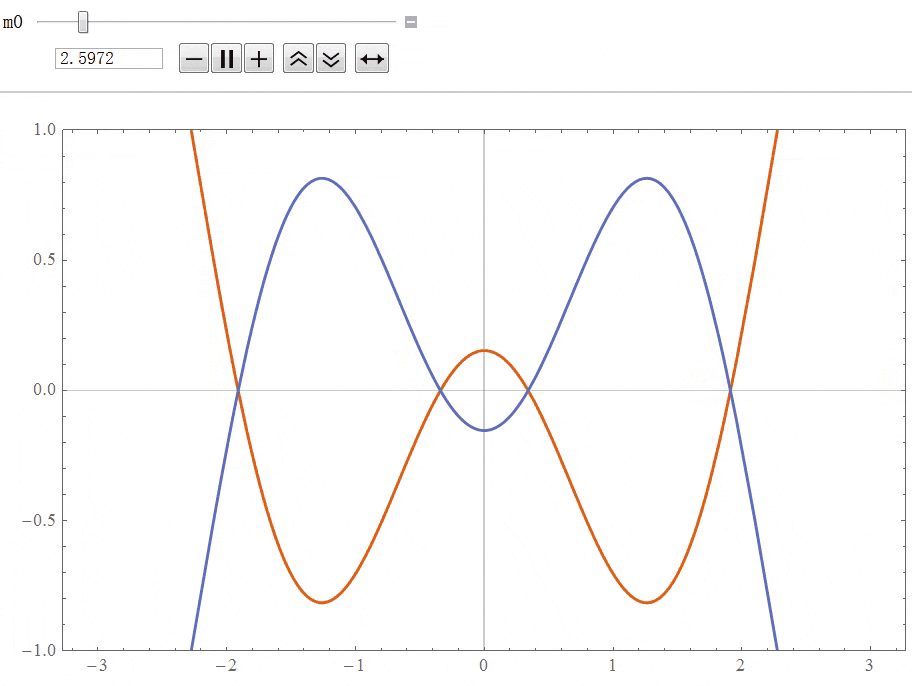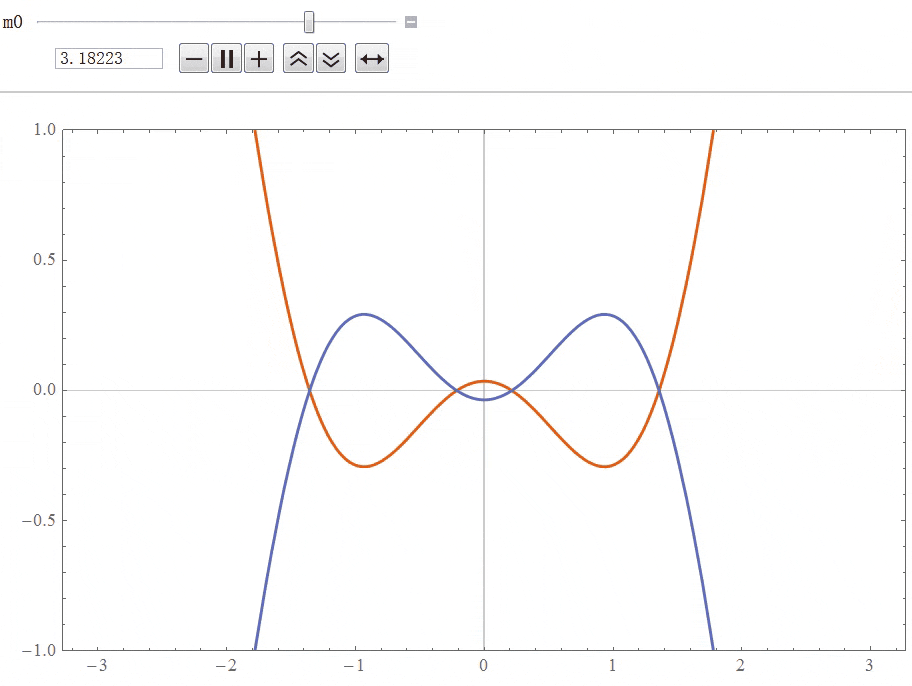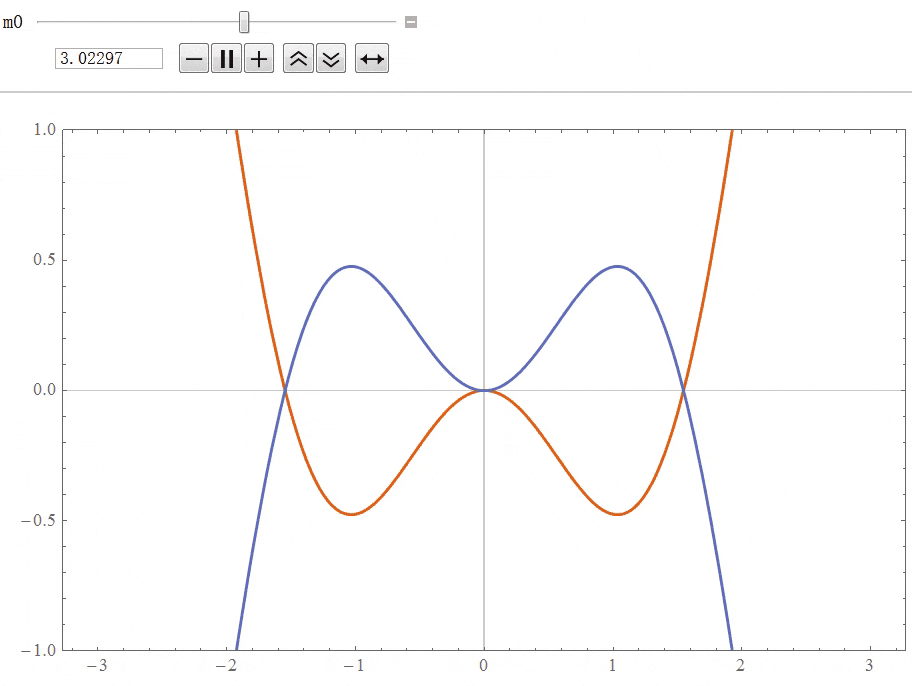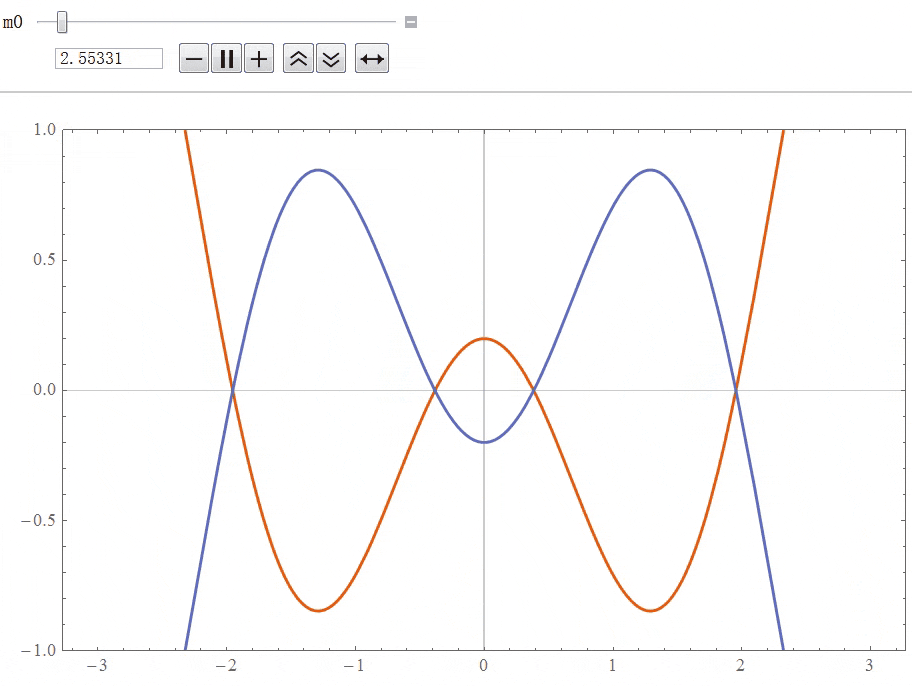
2. 三维体系的势垒散射
考虑电子入射于一个与赝自旋无关的方势垒![]() ,其中
,其中
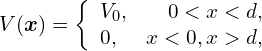
输运方向是沿着两个圈中心连线的方向,即![]() 方向。
方向。
定义净圈透射率(net loop transmission, NLT):
![]()
定义圈极化率(loop polarization rate):
![]()
由于势垒与![]() 和
和![]() 无关,因此在这两个方向上动量守恒,所以三维散射问题可以约化为一系列以
无关,因此在这两个方向上动量守恒,所以三维散射问题可以约化为一系列以![]() 和
和![]() 作为参数的一维散射问题。
作为参数的一维散射问题。
在此基础上,我们可以对选取不同的![]() 和
和![]() 进行分类讨论。
进行分类讨论。![]() 和
和![]() 空间的示意图如下:
空间的示意图如下:
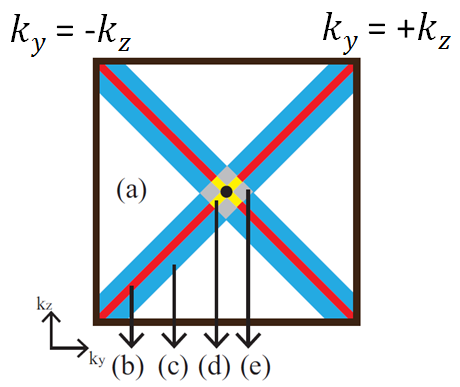
主要分为以下三部分进行讨论:
- 电子垂直入射:中间黑点 ky=kz=0.
- 电子大角度偏离垂直入射:
(b)红色的线:电子态在某个圈平面上,有相对大的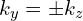 值。
值。
(c)蓝色的区域:电子态靠近某个圈平面上,有相对大的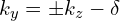 值(其中δ是小量) 。
值(其中δ是小量) 。 - 电子小角度偏离垂直入射:
(d)黄色的线:电子态在某个圈平面上,有相对小的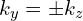 值。
值。
(e)灰色的区域:电子态靠近某个圈平面上,有相对小的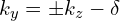 值(其中δ是小量)。
值(其中δ是小量)。
选取不同的![]() 和
和![]() 值时,对应的
值时,对应的![]() 能带图:
能带图:
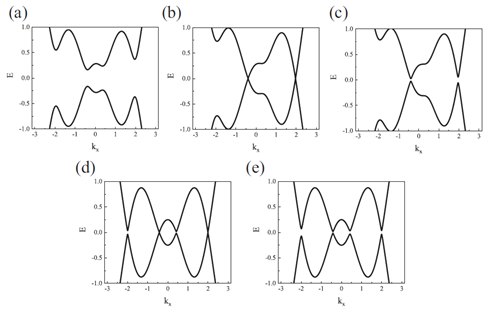
2.1 电子垂直入射
当![]() ,哈密顿量简化为
,哈密顿量简化为
![]()
赝自旋本征值:![]() 或
或![]() 。在下图能带中,实线和虚线分别代表携带不同的赝自旋。如果不翻转赝自旋,具有不同赝自旋本征值的电子态之间不能发生散射。在赝自旋守恒的限制下,相互嵌套和非相互嵌套的情况对应着不同的散射过程,分别为(e)和(f)。
。在下图能带中,实线和虚线分别代表携带不同的赝自旋。如果不翻转赝自旋,具有不同赝自旋本征值的电子态之间不能发生散射。在赝自旋守恒的限制下,相互嵌套和非相互嵌套的情况对应着不同的散射过程,分别为(e)和(f)。
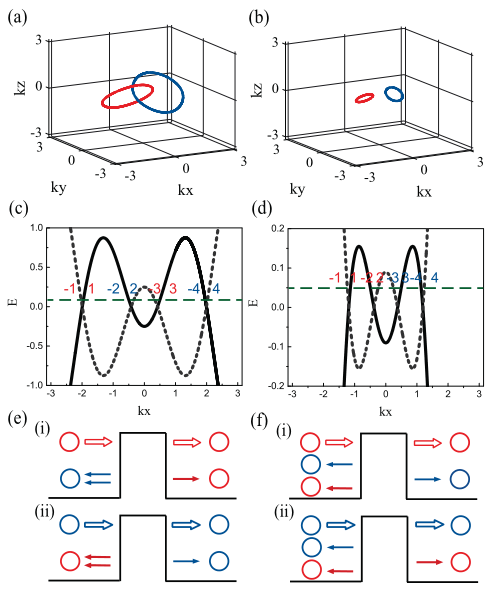
势垒散射结果为:
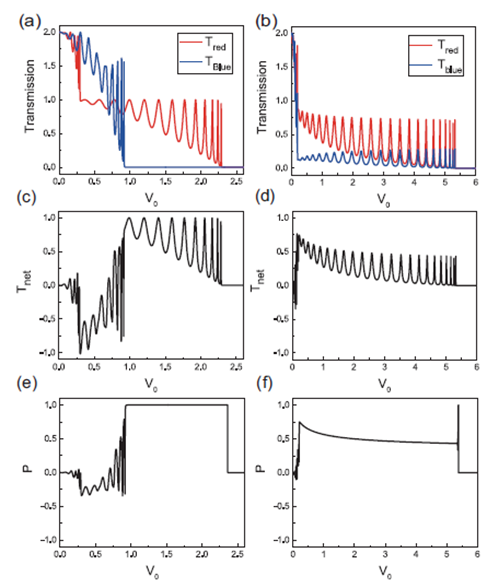
结论:对于垂直入射的情况,圈电子的势垒散射贡献了圈极化率。
2.2 电子非垂直入射
这里考虑的非垂直入射只是在圈平面上,即![]() 。示意图如下(以相互嵌套的情况为例):
。示意图如下(以相互嵌套的情况为例):
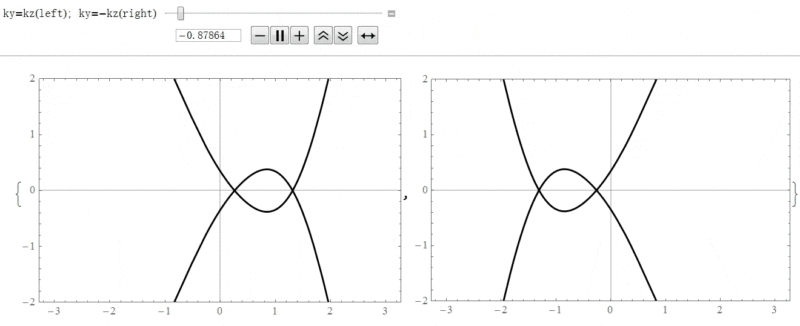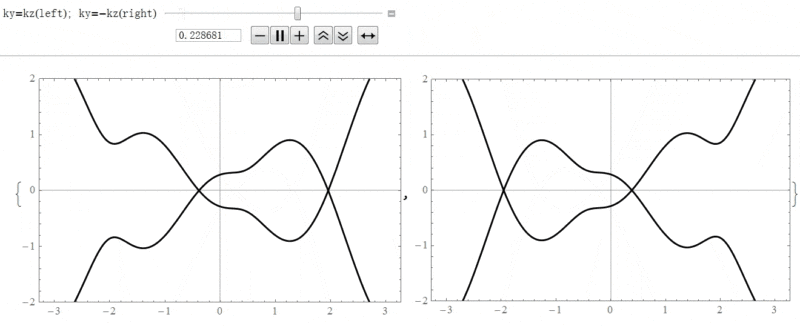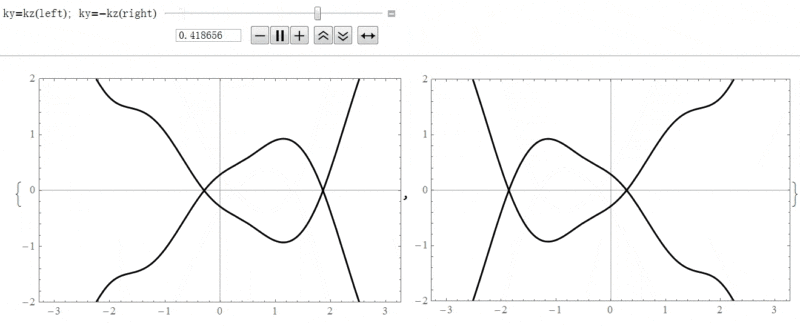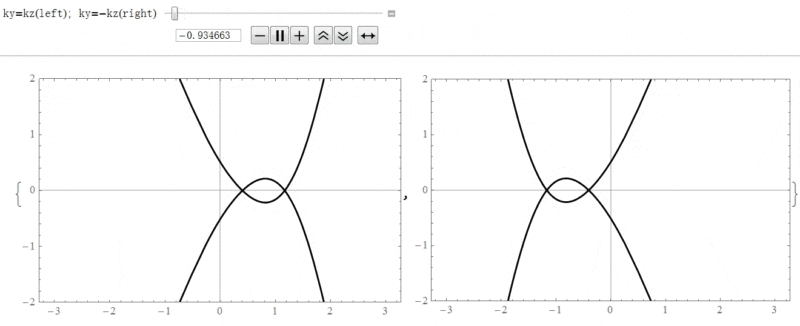
对于小角度偏离圈平面的情况,即![]() ,结论与电子态在圈平面
,结论与电子态在圈平面![]() 的类似(之后会提到)。对于大角度偏离圈平面时,子体系
的类似(之后会提到)。对于大角度偏离圈平面时,子体系![]() 的能带存在带隙,因此不贡献可传播的圈电子。
的能带存在带隙,因此不贡献可传播的圈电子。
接下来,对于在圈平面上的电子,我将分为“大角度偏离垂直入射”和“小角度偏离垂直入射”进行讨论。
2.2.1 大角度偏离垂直入射(相对大的k_y=\pm k_z值)
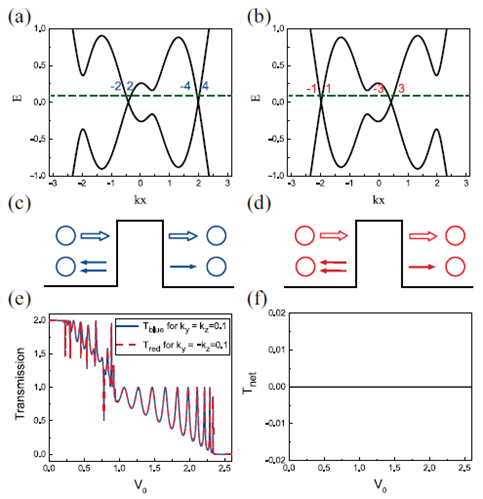
由于存在以下这两个条件:
(1)![]() 和
和![]() 是由两组相互独立的电子态贡献的。
是由两组相互独立的电子态贡献的。
(2)两个圈平面对应的子体系具有镜面对称
![]()
因此,这种情况圈电子的势垒散射结果只贡献电导值,不贡献圈极化率。
当入射电子微小偏离圈平面时,镜面对称性对称性仍然有:
![]()
2.2.2 小角度偏离垂直入射(相对小的k_y=\pm k_z值)
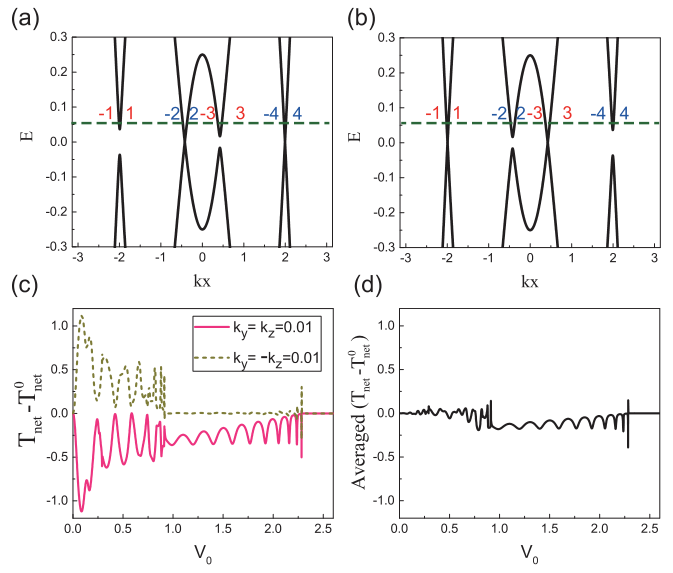
平均净圈透射率:
![]()
从图(d)可以看出,经过平均后,大部分偏离垂直入射的差值刚好相互抵消。因此这种情况圈电子的势垒散射结果与垂直入射的结果相近,贡献圈极化率。
此外,剩余不能被完全抵消的小量来源于两个圈上的电子态之间发生了在垂直入射时因为赝自旋守恒而被禁止的散射过程。
当入射电子微小偏离圈平面时,结论类似。
这里对第二部分的内容做个总结:
- 下图中的(a)区域即不贡献电导,也不贡献圈极化率。
- 下图中的(b)和(c)只贡献电导,不贡献圈极化率。
- 下图中的(d)和(e)既贡献电导,也贡献圈极化率,同时平均的极化情况与垂直入射(中心黑点)的结果相近。

3. 考虑有限宽度的平板(Slab)
以上讨论基于可约化为一维散射问题的情况(体系尺寸无穷大)。在实际的量子输运电子器件和测量中,通常考虑的是一个有横截面积的准一维体系(bar)。
然而在有限横截面积的情况下,有限尺寸效应会使得霍普夫半金属打开带隙。此外,对于准一维体系,能带结构会十分复杂,两个圈对应的子能带会相互交织在一块,使得计算上难以直接分辨出来电子态属于哪个圈。
因此这里只是考虑在某个方向上为有限宽度的情况(slab),例如![]() 方向上为有限宽度
方向上为有限宽度![]() 。
。
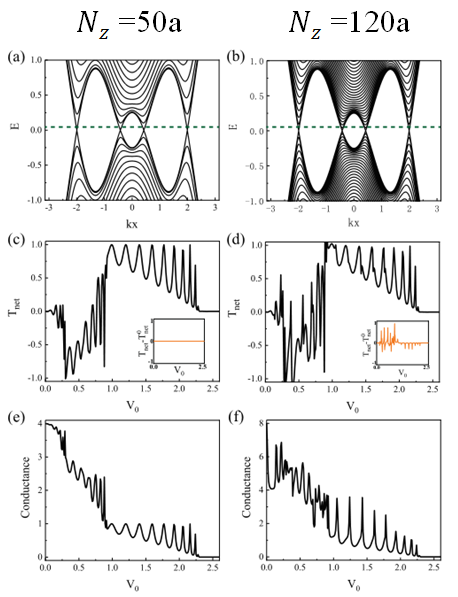
这里令![]() 。若
。若![]() 不为零,对应的子体系会打开带隙,是平庸的绝缘态。
不为零,对应的子体系会打开带隙,是平庸的绝缘态。
通过观察可以发现:只有垂直入射的电子态贡献净圈透射率(net loop transmission)。当增加![]() ,电导值增加,但净圈透射率保持不变,导致了圈极化率的降低。这个结论与上一部分的结论相吻合。
,电导值增加,但净圈透射率保持不变,导致了圈极化率的降低。这个结论与上一部分的结论相吻合。
需要说明的是:这里圈极化率的降低是十分缓慢的,这是由于在半金属零能附近的电子态密度(DOS)比较低。
4. 在y方向上的输运情况
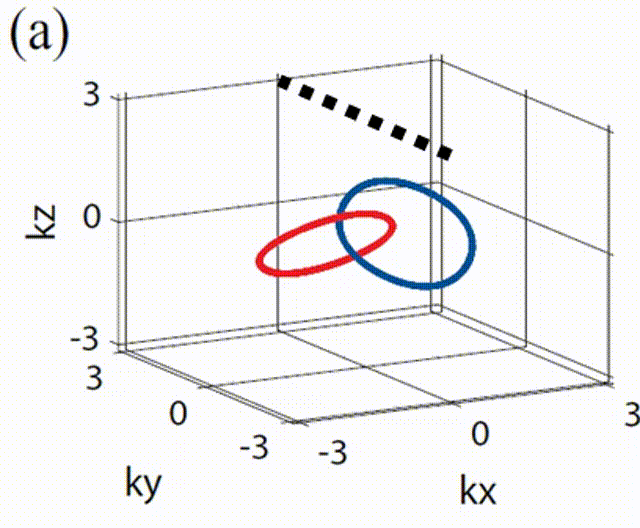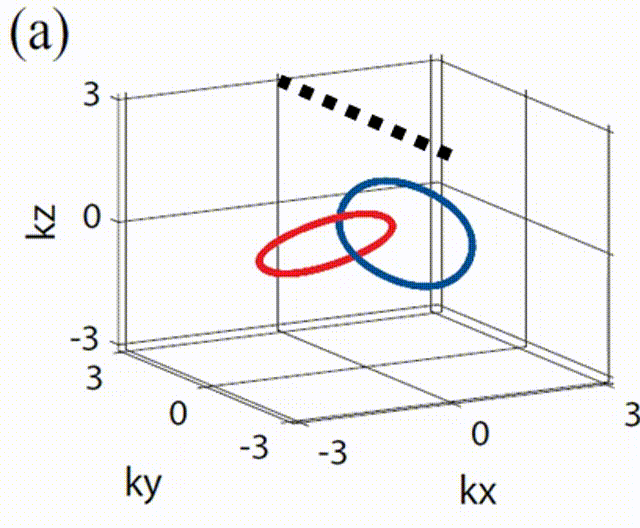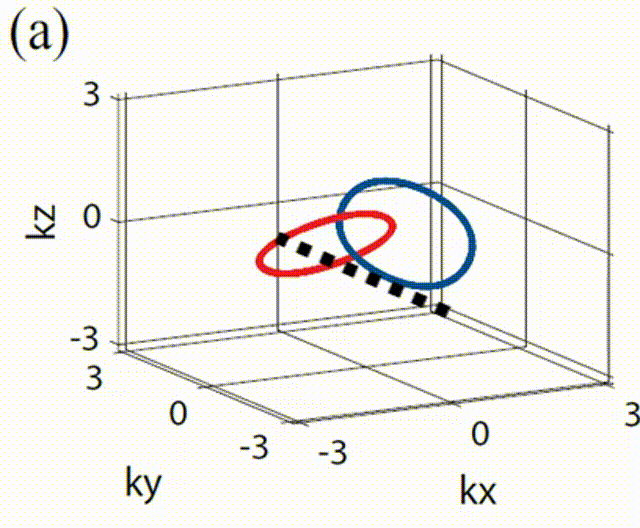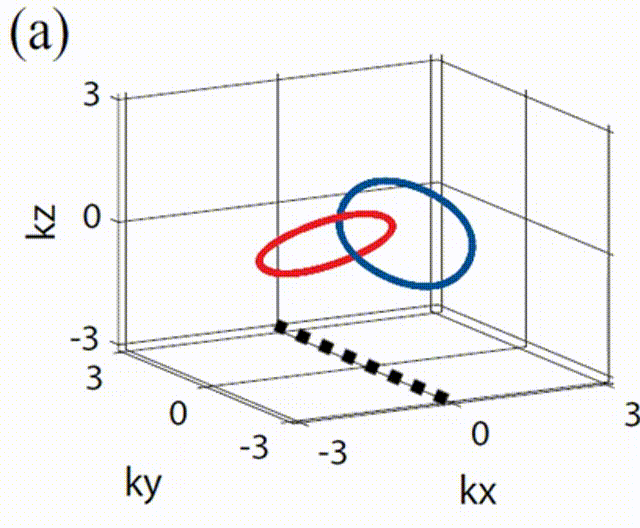
上面讨论的是沿着x方向上的输运。由于霍普夫半金属具有各项异性,这里还考虑了其他方向上的输运,例如y方向。通过下图,可以找到蓝圈和红圈的共同![]() 窗口。由于上下对称,两个窗口的中心分别是
窗口。由于上下对称,两个窗口的中心分别是![]() 和
和![]() 。
。
这两个窗口中心对应的能带和势垒散射结果为:
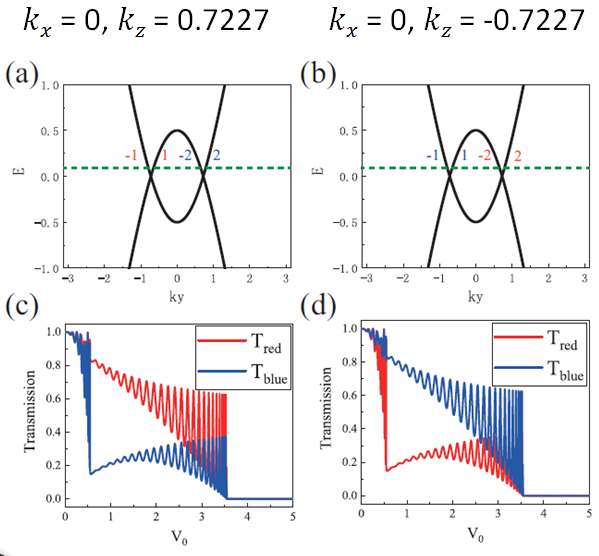
结论是平均后的净圈透射率为0,这是由于存在以下对称性:
![]()
此外,对于更一般的情况(包括两个圈非共同的![]() 区域),存在以下对称性:
区域),存在以下对称性:
![]()
因此,沿着y方向的输运散射结果整体是不贡献圈极化的。
5. 无序诱导的圈极化
由于垂直入射的电子在圈极化中扮演着重要角色,因此为了简化问题,这里的无序散射的研究仅基于垂直入射的情况。同时无序也是仅仅是考虑在x方向上的无序,如图(a)所示。
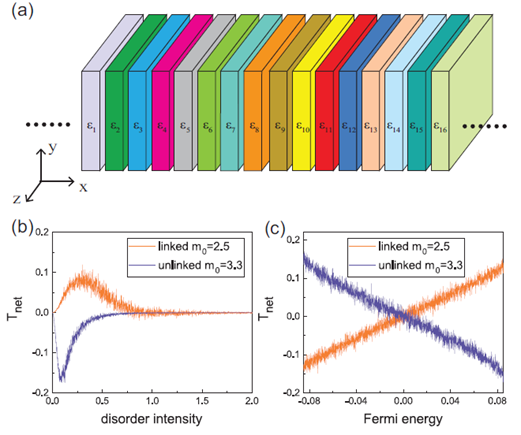
我们发现:对于相互嵌套和非相互嵌套两种情况,无序诱导的圈极化朝向不同的方向。这是由于最近邻的圈态在动量转移散射的过程中起着主要作用,同时对于相互嵌套和非相互嵌套两种情况,最近邻的圈态相对位置发生了变化,如下图所示。

无序诱导圈极化的原因:两个圈自由度本身是镜像对称的,但从输运通道的角度来说不是镜面对称的,因为向右传播的通道在镜面对称之后,成为了向左传播的通道。因此在散射过程中,两个圈之间有了净的动量转移差,导致了圈极化。
可参考无序诱导的谷极化:Phys. Rev. Lett. 118, 096602 (2017)。
例如,考虑最近邻的圈态:
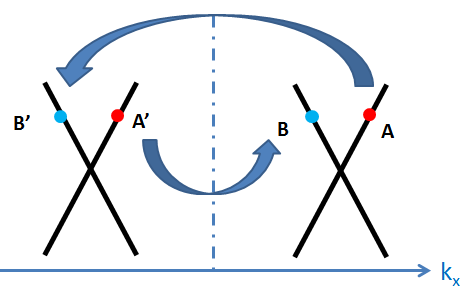
![]() 和
和![]() 的散射过程有一个净的动量转移差(输运通道不是镜面对称的)。
的散射过程有一个净的动量转移差(输运通道不是镜面对称的)。
6. 光滑势的影响
高斯势垒:
![]()
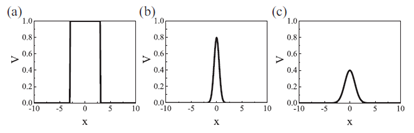
高斯无序(一系列随机分布的光滑高斯势):
![]()
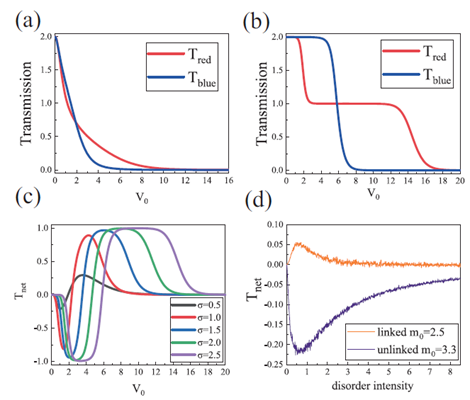
光滑势垒可以抑制大动量转移的散射,因此在一定的势垒高度范围内更容易实现克莱因隧穿(Klein tunneling)。
7. 圈过滤器或圈探测器
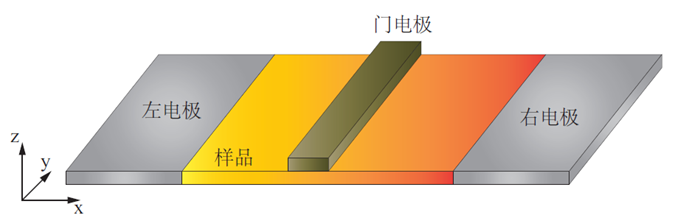
以上是实验装置图。在有限宽度的平板(slab)中,当宽度较小时,垂直入射的电子贡献了所有的圈极化率和电导。因此,我们可以利用光滑势垒的散射实现圈过滤器和圈探测器(loop filter and loop detector)。
原理图为:
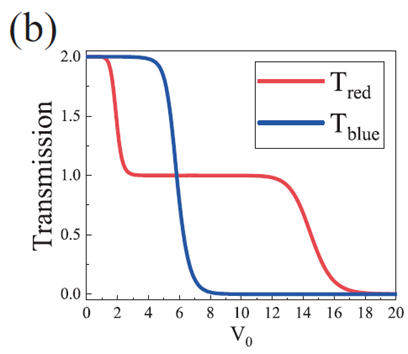
首先测量不加门电压时的电导![]() :
:
![]()
加门电压产生光滑势垒,这时所有蓝圈的通道的输运仍然是鲁棒的,但红圈通道减少了一半。电导![]() :
:
![]()
于是可以得到:
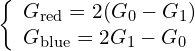
8. 技术细节
(1)通道分辨的透射率和反射率的计算方法参考:模式匹配方法计算散射矩阵(附Python代码)。
(2)由于霍普夫半金属模型中存在次近邻项,因此在上面的计算中如果选取两倍元胞时,会出现能带折叠的现象。因此在区分蓝圈和红圈的电子态时,需要把能带“反折叠”回去,找到对应的圈电子态。
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】