Ising (伊辛)模型为:![]()
这里要用到Metropolis采样,可看这篇文章:Metropolis采样 (附Python代码)。
代码主要参考资料[1], 是采用XY Ising模型。自己有做了些改动和注释,看起来会更容易些。代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/1249
"""
import random
import matplotlib.pyplot as plt
import numpy as np
import copy
import math
import time
def main():
size = 30 # 体系大小
T = 2 # 温度
ising = get_one_sample(sizeOfSample=size, temperature=T) # 得到符合玻尔兹曼分布的ising模型
plot(ising) # 画图
energy_s = []
for i in range(size):
for j in range(size):
energy_s0 = getEnergy(i=i, j=j, S=ising) # 获取格点的能量
energy_s = np.append(energy_s, [energy_s0], axis=0)
plt.hist(energy_s, bins=50, density=1, facecolor='red', alpha=0.7) # 画出格点能量分布 # bins是分布柱子的个数,density是归一化,后面两个参数是管颜色的
plt.show()
def get_one_sample(sizeOfSample, temperature):
S = 2 * np.pi * np.random.random(size=(sizeOfSample, sizeOfSample)) # 随机初始状态,角度是0到2pi
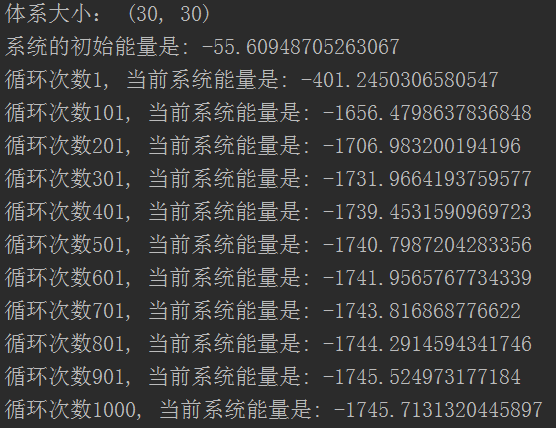
print('体系大小:', S.shape)
initialEnergy = calculateAllEnergy(S) # 计算随机初始状态的能量
print('系统的初始能量是:', initialEnergy)
newS = np.array(copy.deepcopy(S))
for i00 in range(1000): # 循环一定次数,得到平衡的抽样分布
newS = Metropolis(newS, temperature) # Metropolis方法抽样,得到玻尔兹曼分布的样品体系
newEnergy = calculateAllEnergy(newS)
if np.mod(i00, 100) == 0:
print('循环次数%i, 当前系统能量是:' % (i00+1), newEnergy)
print('循环次数%i, 当前系统能量是:' % (i00 + 1), newEnergy)
return newS
def Metropolis(S, T): # S是输入的初始状态, T是温度
delta_max = 0.5 * np.pi # 角度最大的变化度数,默认是90度,也可以调整为其他
k = 1 # 玻尔兹曼常数
for i in range(S.shape[0]):
for j in range(S.shape[0]):
delta = (2 * np.random.random() - 1) * delta_max # 角度变化在-90度到90度之间
newAngle = S[i, j] + delta # 新角度
energyBefore = getEnergy(i=i, j=j, S=S, angle=None) # 获取该格点的能量
energyLater = getEnergy(i=i, j=j, S=S, angle=newAngle) # 获取格点变成新角度时的能量
alpha = min(1.0, math.exp(-(energyLater - energyBefore)/(k * T))) # 这个接受率对应的是玻尔兹曼分布
if random.uniform(0, 1) <= alpha:
S[i, j] = newAngle # 接受新状态
else:
pass # 保持为上一个状态
return S
def getEnergy(i, j, S, angle=None): # 计算(i,j)位置的能量,为周围四个的相互能之和
width = S.shape[0]
height = S.shape[1]
top_i = i - 1 if i > 0 else width - 1 # 用到周期性边界条件
bottom_i = i + 1 if i < (width - 1) else 0
left_j = j - 1 if j > 0 else height - 1
right_j = j + 1 if j < (height - 1) else 0
environment = [[top_i, j], [bottom_i, j], [i, left_j], [i, right_j]]
energy = 0
if angle == None:
for num_i in range(4):
energy += -np.cos(S[i, j] - S[environment[num_i][0], environment[num_i][1]])
else:
for num_i in range(4):
energy += -np.cos(angle - S[environment[num_i][0], environment[num_i][1]])
return energy
def calculateAllEnergy(S): # 计算整个体系的能量
energy = 0
for i in range(S.shape[0]):
for j in range(S.shape[1]):
energy += getEnergy(i, j, S)
return energy/2 # 作用两次要减半
def plot(S): # 画图
X, Y = np.meshgrid(np.arange(0, S.shape[0]), np.arange(0, S.shape[0]))
U = np.cos(S)
V = np.sin(S)
plt.figure()
plt.quiver(X, Y, U, V, units='inches')
plt.show()
if __name__ == '__main__':
main()
计算结果,得到某个样品(温度![]() ):
):
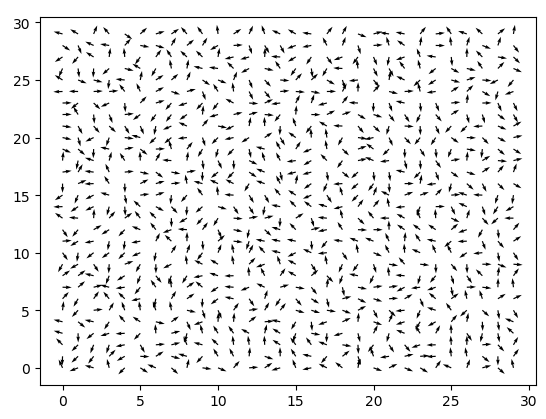
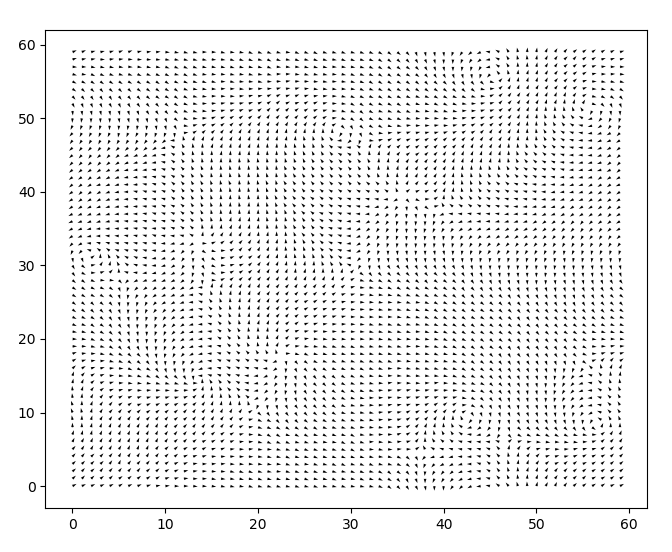
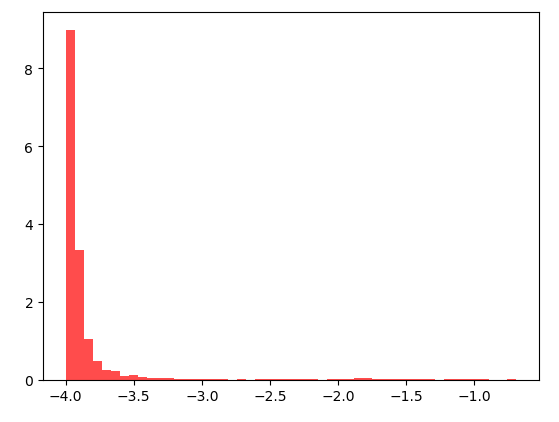
能量分布为:
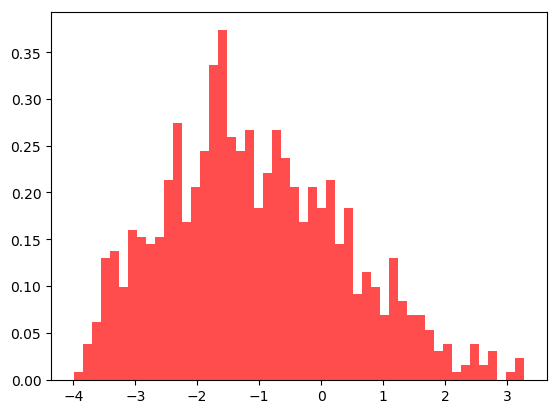
收敛情况为:
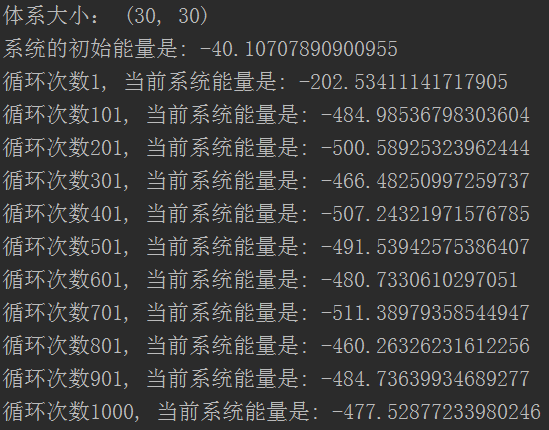
温度![]() 的情况,结果为:
的情况,结果为:
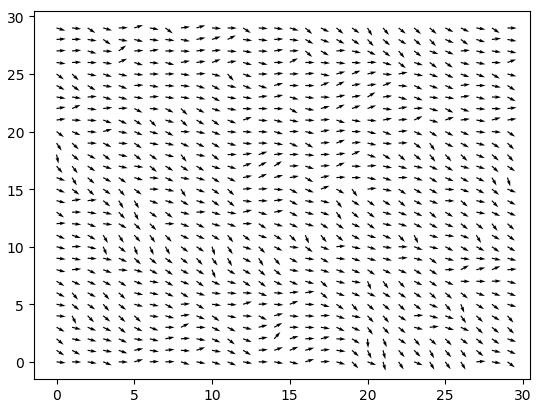
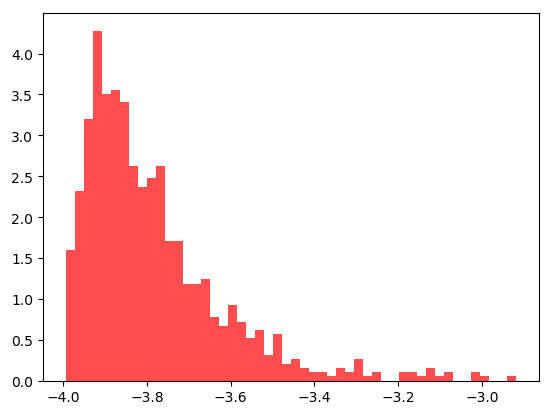
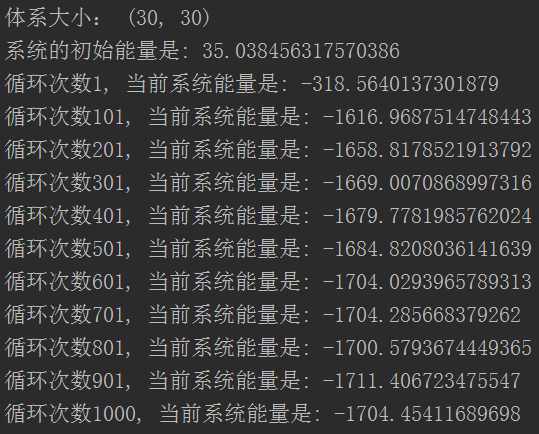
温度![]() 的情况,结果为:
的情况,结果为:
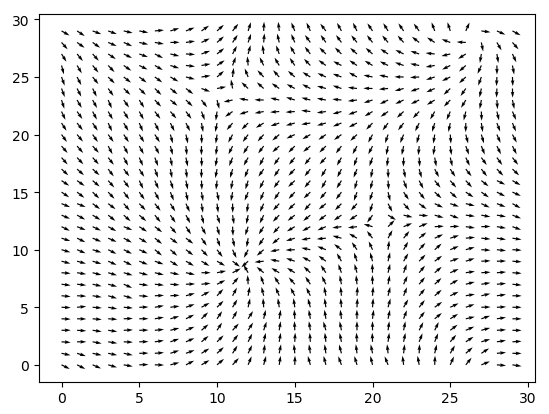
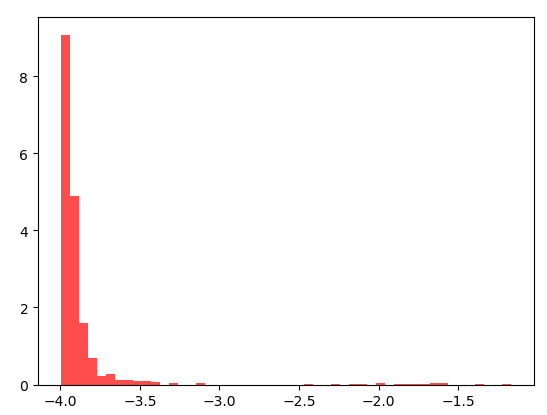
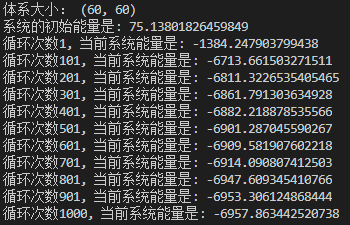
长和宽改为60, 温度为![]() 情况,结果为:
情况,结果为:
把程序修改为只有spin-up, spin-down两种状态,计算不同温度下的总磁矩,可得到转变温度。程序为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/1249
"""
import random
import matplotlib.pyplot as plt
import numpy as np
import copy
import math
import time
def main():
size = 30 # 体系大小
for T in np.linspace(0.02, 5, 100):
ising, magnetism = get_one_sample(sizeOfSample=size, temperature=T)
print('温度=', T, ' 磁矩=', magnetism, ' 总能量=', calculateAllEnergy(ising))
plt.plot(T, magnetism, 'o')
plt.show()
def get_one_sample(sizeOfSample, temperature):
newS = np.zeros((sizeOfSample, sizeOfSample)) # 初始状态
magnetism = 0
for i00 in range(100):
newS = Metropolis(newS, temperature)
magnetism = magnetism + abs(sum(sum(np.cos(newS))))/newS.shape[0]**2
magnetism = magnetism/100
return newS, magnetism
def Metropolis(S, T): # S是输入的初始状态, T是温度
k = 1 # 玻尔兹曼常数
for i in range(S.shape[0]):
for j in range(S.shape[0]):
newAngle = np.random.randint(-1, 1)*np.pi
energyBefore = getEnergy(i=i, j=j, S=S, angle=None) # 获取该格点的能量
energyLater = getEnergy(i=i, j=j, S=S, angle=newAngle) # 获取格点变成新角度时的能量
alpha = min(1.0, math.exp(-(energyLater - energyBefore)/(k * T))) # 这个接受率对应的是玻尔兹曼分布
if random.uniform(0, 1) <= alpha:
S[i, j] = newAngle # 接受新状态
else:
pass # 保持为上一个状态
return S
def getEnergy(i, j, S, angle=None): # 计算(i,j)位置的能量,为周围四个的相互能之和
width = S.shape[0]
height = S.shape[1]
top_i = i - 1 if i > 0 else width - 1 # 用到周期性边界条件
bottom_i = i + 1 if i < (width - 1) else 0
left_j = j - 1 if j > 0 else height - 1
right_j = j + 1 if j < (height - 1) else 0
environment = [[top_i, j], [bottom_i, j], [i, left_j], [i, right_j]]
energy = 0
if angle == None:
for num_i in range(4):
energy += -np.cos(S[i, j] - S[environment[num_i][0], environment[num_i][1]])
else:
for num_i in range(4):
energy += -np.cos(angle - S[environment[num_i][0], environment[num_i][1]])
return energy
def calculateAllEnergy(S): # 计算整个体系的能量
energy = 0
for i in range(S.shape[0]):
for j in range(S.shape[1]):
energy += getEnergy(i, j, S)
return energy/2 # 作用两次要减半
if __name__ == '__main__':
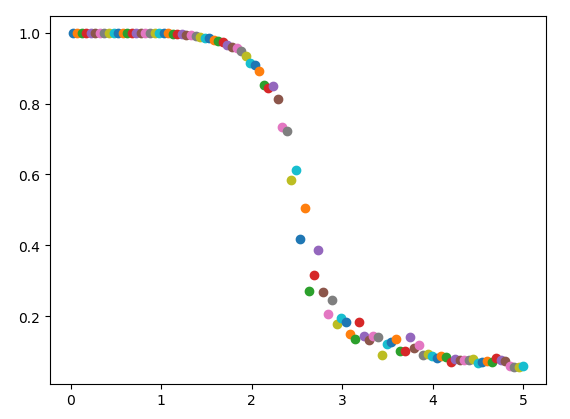
main()结果为(磁矩随温度的变化关系):
参考资料:
[1] 蒙特卡洛模拟Ising模型
[2] 集智百科:ISING模型
[3] https://zh.wikipedia.org/wiki/%E6%98%93%E8%BE%9B%E6%A8%A1%E5%9E%8B
[4] python:二维正方形晶格Ising模型的 Monte Carlo 模拟
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
大佬,可以问下为什么你求magnetism的代码不是达到平衡态之后,再进行进行一系列mcmc过程求解magnetism的平均值,而是从第一个就开始求解magtism的平均值了
计算新的状态,需要原先的状态和能量值吧。
你好,请问ising模型模拟中,比如再第二个只有spin-up down的代码中,虽说是四方晶格,但是为什么不需要磁交换等参数,那博主您这模型是模拟的哪个物质的呢?或者说,如果我想用您的代码模拟一个特定的物质,需要改动哪部分?
这个是一个理想化的模型,没有指定某个物质。我目前没做这方面的研究,具体不是很了解,你可以找些文献看看,可能也有相关的计算软件。
大佬,计算(i,j)位置的能量,为周围四个的相互能之和,得出的environment矩阵是某一环境的周围环境吗?比如我用3*3的体系,(1,1)这个环境周围的四个环境是(2,1),(1,0),(0,1),(1,2)吗?但是计算的结果显示并不是这四个环境?还是代码在这一块怎么解决的,感觉理解不了
嗯,几何坐标是这个情况。在代码中具体怎么体现和编号有关系,如果按照几何坐标来编号,则完全对应。
理解了,谢谢大佬
博主,请问“计算(i,j)位置的能量,为周围四个的相互能之和”这一步为什么用 energy += -np.cos(S[i, j] - S[environment[num_i][0], environment[num_i][1]])来求,初学者,在这一步看得不是很明白,可以讲一下其中的原理和计算过程吗?感谢
你是指为什么用cos吗?这里根据角度差来定义能量,当同向时能量是最小的。在下面的评论区有类似的提问和回答。
博主,为什么状态更新后不是依据整个体系的能量而是依据被改变的这个自旋的能量来进行接受采样啊?
是每个自旋能量的分布呈现出玻尔兹曼分布。把玻尔兹曼分布代入公式,就得到了接受率表达式。
嗯嗯,把玻尔兹曼分布代入公式得到接受率的这部分我理解。是前面的那部分,即每个自旋的能量分布呈现玻尔兹曼分布这里,玻尔兹曼分布不是描述的一个configuration出现的概率分布吗?如果是一个configuration中的单个自旋来表达玻尔兹曼分布(其中能量通过这个自旋和邻居间的相互作用来计算),那是如何保证最后configuration出现的概率是服从玻尔兹曼分布呢?是因为中心极限定理吗?
麦克斯韦-玻尔兹曼分布是一个描述一定温度下微观粒子运动速度的概率分布,不是系统总能量的分布。在固定温度下,系统的总能量是固定的。
为什么get_energy那里是np.cos
当角度差为0时,np.cos的值最大,前面加一个负号,所以能量是最小的。-cos的形状刚好与能量与角度的关系吻合,所以用-cos。
但是当相差2π时,np.cos也是最大
相差2π,属于同一个角度
明白了,谢谢答主,答主可以解释一下那个能量为什么要除以2嘛,我代码基础比较差,还有energy中那个np.cos里面具体怎么运算的,非常感谢您!
除以2是因为对所有格点能量相加时,相互作用的能量加了两次,例如A和B的作用、B和A的作用,应该只要算一次。np.cos是余弦函数呀,括号里面是角度相减。
答主,还有一个问题,就是在方向只有向上或者向下的时候,那个能量计算结果应该是整数,但是我的都是小数,麻烦你能解答一下嘛
是否应该是整数这个我不清楚。你可以把程序的中间结果输出,例如每个能量的数值都输出,这样很容易就可以找出是哪里的问题
收到,谢谢您
有没有 求 Heisenberg 模型 代码
我没算过,目前不做这个方向,这个也是随便写写。你可以试着把代码改成Heisenberg模型。
大佬,在低温下的XY Ising模型中会出现涡流这现象,请问有什么简便有效的方法可以识别出所有涡流么?
我没有试过这个。最简单的方法就是用眼睛看了,明显的涡流能够直接看出来。如果要用程序写的话,可以从每一点出发,根据流的大概方向走,如果回到原先的点,存在循环的现象,就说明附近有涡流了。多个循环现象可能对应的只是一个涡流。