原文
- Ji-Huan Guan, Yan-Yang Zhang*, Wei-Er Lu, Yang Xia and Shu-Shen Li, Barrier tunneling of the loop-nodal semimetal in the hyperhoneycomb lattice. J. Phys.: Condens. Matter 30, 185402 (2018).
评价:超蜂窝结构不仅在几何维度上拓展了二维的六角蜂窝结构,同时也将“狄拉克点”拓展到了“狄拉克节线”。该工作的主要价值体现在研究了狄拉克节线附近类似于狄拉克费米子的特性。此外,发现了狄拉克节线有自身的一些独特性质,例如:当费米能接近零能时,几乎在整个狄拉克圈平面上都具有鲁棒的量子输运性质。
摘要
超蜂窝(hyperhoneycomb)结构是六角蜂窝结构在三维上的拓展。六角蜂窝结构对应的石墨烯是是一种节点半金属;而超蜂窝结构在仅仅考虑s轨道时是一种节线半金属。本文通过对节线半金属局域有效哈密顿量的解析讨论,以及超蜂窝晶格紧束缚模型的严格数值求解,发现在节线圈附近的准粒子由于线性的色散关系,具有与狄拉克/外尔半金属类似的鲁棒量子输运性质。
主要结论为:超蜂窝晶格的节线平面内,大范围的方位角中都存在着克莱因隧穿(Klein tunneling),而蜂窝晶格仅仅在垂直角度中存在克莱因隧穿;在超蜂窝晶格偏离节线平面,极角方向的势垒散射类似于蜂窝晶格中的手征隧穿(chiral tunneling)。
1. 超蜂窝晶格模型
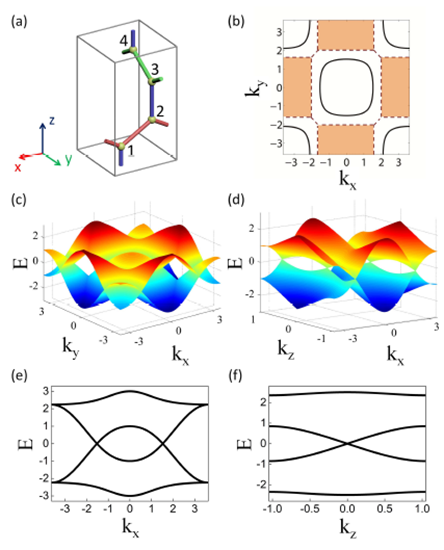
超蜂窝晶格紧束缚哈密顿量在倒空间中写为:
![]()
其中,
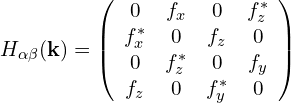
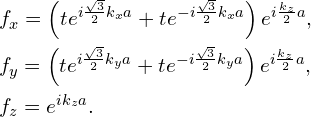
零能解(节线圈方程):
![]()
2. 局域有效哈密顿量
为了研究节圈附近的准粒子性质,我们采用一个![]() 的局域有效哈密顿量。该哈密顿量是由超蜂窝紧束缚模型哈密顿量投影到一个二分量的子空间,表示了节圈附近最低的两个带,与狄拉克哈密顿量类似具有线性的色散关系。基于该哈密顿量的研究结果将具有一定的普适性。
的局域有效哈密顿量。该哈密顿量是由超蜂窝紧束缚模型哈密顿量投影到一个二分量的子空间,表示了节圈附近最低的两个带,与狄拉克哈密顿量类似具有线性的色散关系。基于该哈密顿量的研究结果将具有一定的普适性。
![]()
其中,
![]()
表示的是从零能处的节线圈![]() (
(![]() ,
,![]() ,
,![]() )上的某个局域点为参考点开始测量,同时具有与参考点相同的方位角
)上的某个局域点为参考点开始测量,同时具有与参考点相同的方位角![]() 。其中
。其中![]() 和
和![]() 满足公式
满足公式![]() 。
。
在每个方位角![]() 上,费米速度
上,费米速度![]() 可以根据数值拟合得到:
可以根据数值拟合得到:
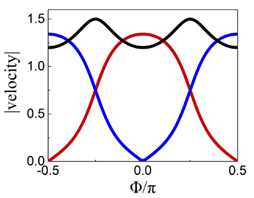
局域有效哈密顿量绕着方位角![]() 旋转一周,可得到完整的节线:
旋转一周,可得到完整的节线:
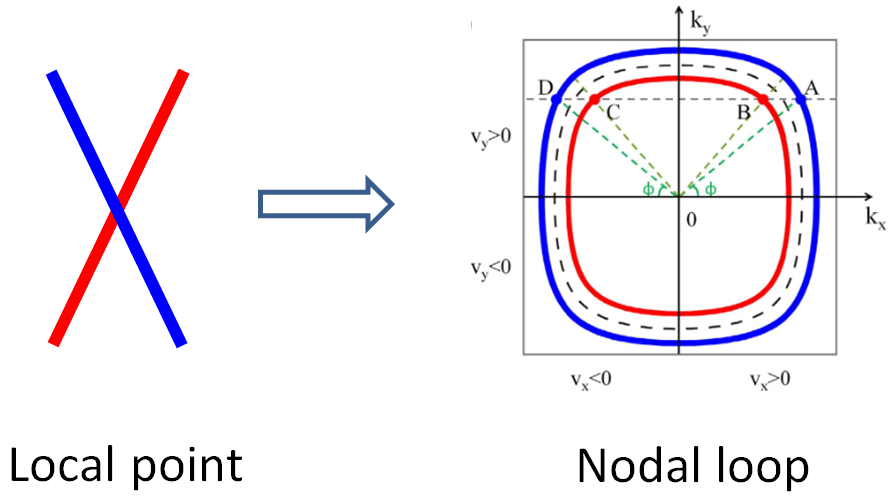
3. 基于局域有效哈密顿量的势垒散射解析
考虑电子入射于一个与赝自旋无关的方势垒![]() ,其中
,其中
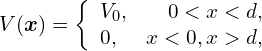
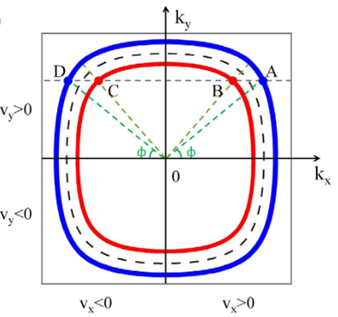
3.1 入射电子的动量方向位于节线圈平面内
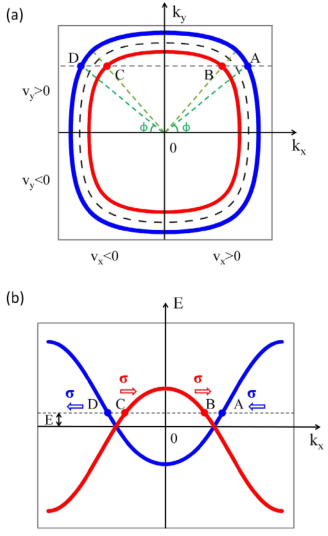
当![]() ,也就是说入射电子的动量
,也就是说入射电子的动量![]() 与节线圈共面,局域有效哈密顿量可以写为
与节线圈共面,局域有效哈密顿量可以写为
![]()
本征值:
![]()
对应的本征矢:
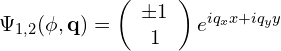
3.1.1 A到B散射过程(反射)
势垒散射的三个区域波函数可以近似写为:
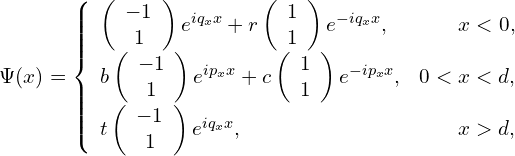
其中,这里把![]() 和
和![]() 以及势垒内外的电子态参考点近似选取在同一个方位角上。在之后的讨论中也多少采取了相同的近似。该近似是合理的,尤其是当费米能接近零能时误差可忽略不计。
以及势垒内外的电子态参考点近似选取在同一个方位角上。在之后的讨论中也多少采取了相同的近似。该近似是合理的,尤其是当费米能接近零能时误差可忽略不计。
通过对波函数在势垒边缘上的匹配,得到透射系数:
![]()
即透射概率为:
![]()
该过程如同一维无质量的狄拉克费米子或者二维无质量狄拉克费米子垂直入射时的克莱因隧穿(Klein tunneling),这是赝自旋守恒的结果。
3.1.2 A到D散射过程(反射)
势垒散射的三个区域波函数可以近似写为:
![Rendered by QuickLaTeX.com \begin{array}{l} \Psi(x)= \left\{ \begin{array}{lr} \left[ \left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{ik_{x}x}+r\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{-ik_{x}x}\right]e^{-ik_{0x}x}, & x<0, \\ \left[b\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{ik_{x}^{\prime}x}+c\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{-ik_{x}^{\prime}x}\right]e^{-ik_{0x}x}, & 0<x<d, \\ \left[t\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{ik_{x}x}\right]e^{-ik_{0x}x},& x>d. \end{array} \right. \end{array}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-2512ae7b6f94a53c0c8fe38188678d85_l3.png)
其中,![]() 和
和![]() 的参考点分别是
的参考点分别是![]() 和
和![]() ,即
,即
![]()
得到透射概率:
![]()
存在共振条件使得![]() :
:
![]()
把式子
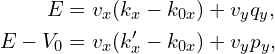
代入共振条件,得到:
![]()
可以看出,随着势垒高度的增加,共振周期保持不变,同时共振周期与势垒宽度![]() 成反比。
成反比。
3.1.3 A到C散射过程(透射)
![]() 和
和![]() 是两个向右的电子态,在解析上我们至少还需要一个的反射态,这里选为
是两个向右的电子态,在解析上我们至少还需要一个的反射态,这里选为![]() 态作为反射态。因为之前的结果表明
态作为反射态。因为之前的结果表明![]() 态散射到
态散射到![]() 态是禁止的,所以
态是禁止的,所以![]() 态是
态是![]() 唯一可能反射到电子态。在势垒内部,向右运动的态有可能是
唯一可能反射到电子态。在势垒内部,向右运动的态有可能是![]() ,也有可能是
,也有可能是![]() 。
。
势垒散射的三个区域波函数可以近似写为:
![Rendered by QuickLaTeX.com \begin{array}{l} \Psi(x)= \left\{ \begin{array}{lr} \left[\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{ik_{x}x}+r\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{-ik_{x}x}\right]e^{-ik_{0x}x}, & x<0, \\ \left[b\left(\begin{array}{c} \mp1 \\ 1 \end{array}\right)e^{\pm ik_{x}^{\prime}x}+c\left(\begin{array}{c} -1 \\ 1 \end{array}\right)e^{-ik_{x}^{\prime}x}\right]e^{-ik_{0x}x}, & 0<x<d, \\ \left[t\left(\begin{array}{c} 1 \\ 1 \end{array}\right)e^{-ik_{x}x}\right]e^{-ik_{0x}x}, & x>d, \end{array} \right. \end{array}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-33b3104fe1ae4e25c515205176a77bee_l3.png)
计算得到透射概率为:
![]()
3.2 入射电子的动量方向偏离节线圈平面
当![]() ,局域有效哈密顿量的本征值为:
,局域有效哈密顿量的本征值为:
![]()
对应的波函数为:
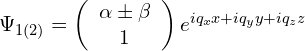
其中,
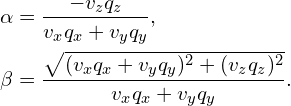
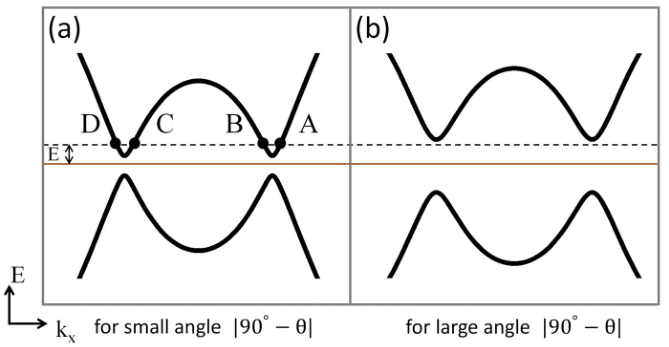
以A到B散射过程为例,同样近似写出势垒散射的三个区域波函数:
![Rendered by QuickLaTeX.com \begin{array}{l} \Psi(x)= \left\{ \begin{array}{lr} \left[\left(\begin{array}{c} \alpha_{1}-\beta_{1} \\ 1 \end{array}\right)e^{iq_{x}x}+r\left(\begin{array}{c} \beta_{1}-\alpha_{1}\\ 1 \end{array}\right)e^{-iq_{x}x}\right]e^{iq_{z}z}, & x<0, \\ \left[b\left(\begin{array}{c} \alpha_{2}-\beta_{2} \\ 1 \end{array}\right)e^{ip_{x}x}+c\left(\begin{array}{c} \beta_{2}-\alpha_{2} \\ 1 \end{array}\right)e^{-ip_{x}x}\right]e^{iq_{z}z}, & 0<x<d, \\ t\left(\begin{array}{c} \alpha_{1}-\beta_{1} \\ 1 \end{array}\right)e^{iq_{x}x+iq_{z}z}, & x>d, \end{array} \right. \end{array}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-f3ac8c4d5d658972a83c61dce6a1fdf3_l3.png)
利用转移矩阵的方法,计算得到透射概率为:
![]()
同样有共振隧穿条件:
![]()
这时A到B可以发生散射,这是由于入射电子的动量方向偏离节线圈平面时,赝自旋不再守恒,类似于石墨烯中的手征散射(chiral scattering)。
4. 基于超蜂窝晶格紧束缚模型的数值计算
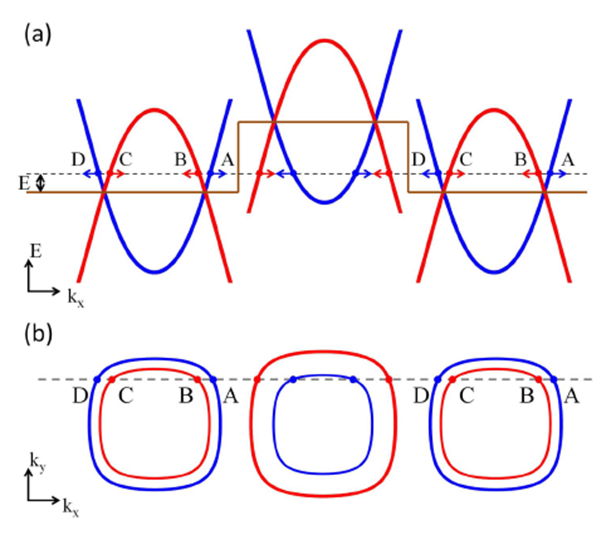
利用通道分辨的透射率和反射率的计算方法:模式匹配方法计算散射矩阵(附Python代码),可以计算得到超蜂窝晶格紧束缚模型中每个通道的散射情况。
4.1 入射电子的动量方向位于节线圈平面内
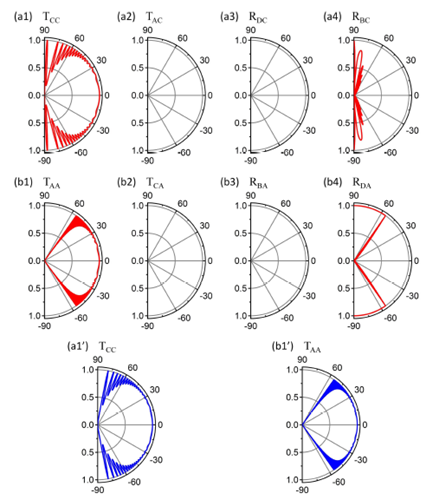
以上散射的结果与解析讨论的结果相吻合,满足赝自旋守恒规则。红色是数值的结果,蓝色的是解析的结果。详细的讨论分析可阅读原文。
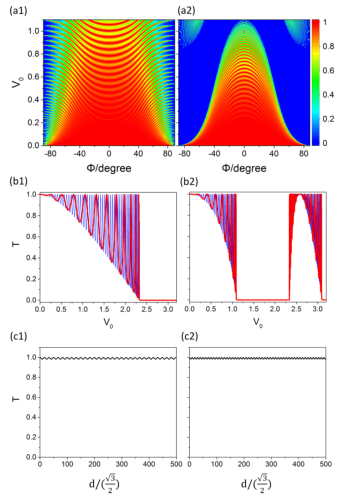
从上图(b1)和(b2)可以看出共振周期与势垒宽度![]() 成反比。从(c1)和(c2)可以看出超蜂窝结构中低能准粒子类似于狄拉克费米子,有鲁棒(robust)的量子输运特性。
成反比。从(c1)和(c2)可以看出超蜂窝结构中低能准粒子类似于狄拉克费米子,有鲁棒(robust)的量子输运特性。
4.2 入射电子的动量方向偏离节线圈平面
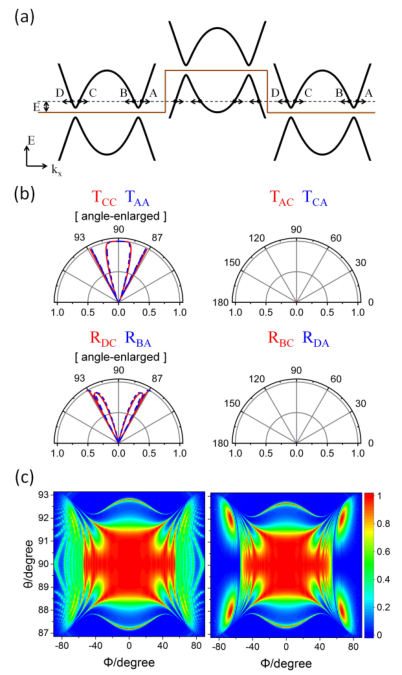
此时赝自旋不再守恒,C到D过程或A到B过程发生了类似于石墨烯中的手征散射。
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
您好 想请问一下这个晶格倒格子空间里紧束缚哈密顿量的胞内hopping为什么也用k表示呢?
傅里叶变换时坐标可以用实际原子坐标,也可以用元胞坐标。两种傅里叶变换的方法都可以的,计算出来的能带都是一样的。用原子坐标时,傅里叶变量元胞内有些跃迁项会增加相位,即e^{ika_{in}};而用元胞坐标时,傅里叶变换元胞内就没有增加相位,即e^{0}。当元胞比较大的时候,一般用元胞的坐标会比较简单。在这个晶格中用原子坐标显得会简洁和对称一些。需要注意的是:在这里如果使用元胞坐标,1和4之间的跃迁要增加一个相位,这个相位包括了z方向和x,y方向的。这是因为上下元胞在x,y方向有个平移。