态密度 density of states

定义

态密度表示的是在单位体积、单位能量内电子的状态数，即

$g(E)=dN/dE=\frac{dN}{dk}\frac{dk}{dE}$

公式推导如下：

1. 倒空间中单位体积内的电子状态数

（1）对于一维的体系，有 $kL=2\pi n$ ，其中L的体系的长度。所以有 $k=\frac{2\pi n}{L}$ 。两个k点之间的间距为 $\triangle k=\frac{2\pi}{L}$ 。

在倒空间的单位体积中有k点个数： $g_k=\frac{L}{2\pi}$ 。

令 $L=1$ ，得到对于实空间的单位体积，倒空间的单位体积中k点的个数： $g_k=\frac{1}{2\pi}$ 。

考虑自旋后，表达式写为： $g_k=\frac{2}{2\pi}$ 。

（2）对于二维的体系，有 $g_k=\frac{2}{(2\pi)^2}$ 。

（3）对于三维的体系，有 $g_k=\frac{2}{(2\pi)^3}$ 。

2. 单位能量中电子状态数

假设能带结构为： $E=\frac{\hbar^2}{2m}k^2$ 。那么有 $k=\frac{\sqrt{2mE}}{\hbar}$ 。

（1）对于一维的体系，在微分能量dE中，k的分布范围是两个线段，体积为 $dV_k=2 dk$ ，因此状态数： $dN=g_k \cdot dV_k=2 dk \frac{2}{2\pi}$ 。

态密度：

$\begin{aligned}g(E)&=dN/dE=\frac{dN}{dk}\cdot\frac{dk}{dE}\\&=2 \frac{2}{2\pi}\cdot \frac{m}{\hbar^2 k}=2 \frac{2m}{2\pi\hbar^2}\cdot \frac{1}{k}\\&=2 \frac{2m}{2\pi\hbar^2}\cdot \frac{\hbar}{\sqrt{2mE}}\\&=2\frac{\sqrt{2m}}{h}\frac{1}{\sqrt{E}}\end{aligned}$

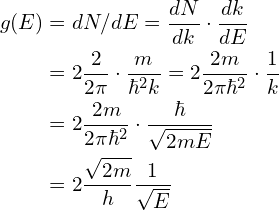
（2）对于二维的体系，在微分能量dE中，k的分布范围是一个环带，体积为 $dV_k=2\pi k dk$ ，因此状态数： $dN=g_k \cdot dV_k=2\pi k dk \frac{2}{(2\pi)^2}$ 。

态密度：

$\begin{aligned}g(E)&=dN/dE=\frac{dN}{dk}\cdot\frac{dk}{dE}\\&=2\pi k\frac{2}{(2\pi)^2} \cdot \frac{m}{\hbar^2 k}\\&=2\pi \frac{2m}{h^2}\cdot 1\\&=\frac{m}{\pi \hbar^2}\end{aligned}$

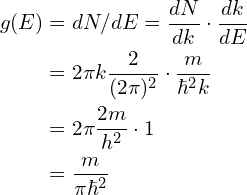
（3）对于三维的体系，在微分能量dE中，k的分布范围是一个球壳，体积为 $dV_k=4\pi k^2 dk$ ，因此状态数： $dN=g_k \cdot dV_k=4\pi k^2 dk\frac{2}{(2\pi)^3}$ 。

态密度：

$\begin{aligned}g(E)&=dN/dE=\frac{dN}{dk}\cdot\frac{dk}{dE}\\&=4\pi k^2\frac{2}{(2\pi)^3}\cdot \frac{m}{\hbar^2 k}=4\pi \frac{2m}{(2\pi)^3\hbar^2}k\\&=4\pi \frac{2m}{(2\pi)^3\hbar^2}\frac{\sqrt{2mE}}{\hbar}\\&=4\pi \frac{(2m)^{\frac{3}{2}}}{h^3}\sqrt{E}\end{aligned}$

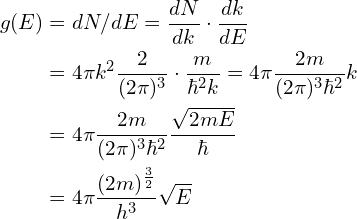
说明：以上几个推导公式仅适用于均匀的倒空间点阵以及简单的能带结构。

参考资料：

[1] 北京科技大学Prof. Xinhe Zheng的半导体物理课件

11,310 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

6 thoughts on “态密度 density of states”

您好，请问对于石墨烯的能带结构，怎么计算他的电子态密度呢？自己没有看明白，来请教一下。

guanjihuan说道：

2023年6月11日 19:24

我目前主要是通过格林函数的方法计算态密度，参考：在方格子、石墨烯中态密度与费米能的关系图（附Python代码）。态密度的定义公式和格林函数的公式应该是等价的。

回复

你好，请问这里说的态密度是指电子实际存在的态的密度还是指电子可能存在的态的密度？

guanjihuan说道：

2022年6月11日 00:37

在量子力学中，波函数就是由各种可能状态的叠加。态密度是在单位体积、单位能量内电子的状态数。
你说的这两种描述好像没什么区别。如果电子完全填充，两者是一样的。如果电子不填充，那么态密度就是当电子填充时最大的状态数了。

回复

请问态密度也可以是实空间的电子密度吗

guanjihuan说道：

2021年9月5日 21:38

态密度有局域态密度（实空间分布）、谱函数（倒空间分布）。实空间的态密度和电子密度好像不完全一样，电子密度可能需要对态密度进行能量上的积分。

回复

态密度 density of states

定义

1. 倒空间中单位体积内的电子状态数

2. 单位能量中电子状态数

Published by guanjihuan

6 thoughts on “态密度 density of states”

发表评论取消回复

定义

1. 倒空间中单位体积内的电子状态数

2. 单位能量中电子状态数

Published by guanjihuan

6 thoughts on “态密度 density of states”

发表评论 取消回复

发表评论取消回复