1. 定义
当一个体系的哈密顿量满足以下条件时,
![]()
即哈密顿量经过某个算符的幺正变换后,可以变为本身哈密顿量加个负号,于是我们可以说该体系具有手征对称性(chiral symmetry),或者也可以称为子晶格对称性(sublattice symmetry),两者是等价的[1]。该算符![]() 被称为手征算符。
被称为手征算符。
2. 能谱
假设![]() 为具有手征对称性的哈密顿量的波函数,对应本征值为
为具有手征对称性的哈密顿量的波函数,对应本征值为![]() ,即
,即
![]()
那么![]() 也是该哈密顿量的波函数,且对应的本征值为
也是该哈密顿量的波函数,且对应的本征值为![]() ,这是因为
,这是因为
![]()
其中,第一步推导用到了上面手征算符的定义。
综上,对于具有手征对称性的体系,能带是上下对称的。
3. 两带体系
接下来考虑一个两带体系,一般哈密顿量写为:
![]()
在两带体系中,手征对称算符可以写为![]() 。如果该哈密顿量满足手征对称性,有
。如果该哈密顿量满足手征对称性,有
![]()
参照博文“矩阵两边乘上向量或者泡利矩阵后的形式”中推导结果可知,![]() 的作用结果是:非对角线的两个元素加上一个负号。所以对于具有手征对称性的两带体系,哈密顿量必须满足:
的作用结果是:非对角线的两个元素加上一个负号。所以对于具有手征对称性的两带体系,哈密顿量必须满足:
![]()
因此,具有手征对称性的两带体系哈密顿量写为:
![]()
或者写成这个形式:
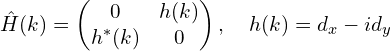
对于一般维度的情况,具有手征对称性的哈密顿量通常有这种形式[2]:
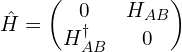
4. 总结
Time-reversal symmetry (T), particle-hole symmetry (P) and chiral symmetry (C) [5,6,7]:

参考资料:
[1] A Short Course on Topological Insulators
[2] https://topocondmat.org/w1_topointro/0d.html
[4] https://openaccess.leidenuniv.nl/bitstream/handle/1887/17678/01.pdf?sequence=7
[5] https://topocondmat.org/w8_general/classification.html
[6] 粒子-空穴对称性 Particle-Hole Symmetry
[7] 时间反演算符 Time Reversal Operator
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
我想请问一下,两能带系统的手征对称算符一定是sigma_z吗?
好像不是唯一的,可能和哈密顿量的表象选取有关,sigma_z 的形式对应的哈密顿量会更直接一些。我没详细研究过,这是我个人的理解,仅供参考。可以考虑阅读文献并搜索关键词 “chiral symmetry” :
[1] Classification of topological insulators and superconductors in three spatial dimensions https://doi.org/10.1103/PhysRevB.78.195125
[2] Classification of reflection-symmetry-protected topological semimetals and nodal superconductors https://doi.org/10.1103/PhysRevB.90.205136
[3] Classification of topological quantum matter with symmetries https://doi.org/10.1103/RevModPhys.88.035005
请问为什么叫“chiral” symmetry?定义式和手性是怎么联系起来的?
这里的chiral symmetry和手性分子的那种结构手性不是完全对应的,属于概念的延伸吧,最早应该是在粒子物理中描述无质量的狄拉克费米子引入的,从波函数的结构上区分了左右,定义了手性/手征。在凝聚态物理中,有类似的准粒子,具有相同的数学结构。
参考:
[1] https://en.wikipedia.org/wiki/Chirality_(physics)#Chiral_symmetry
[2] Chirality和Helicity
关老师,请问,中心反演对称性和手性对称性有什么区别和联系吗,比如打破石墨烯的中心反演对称性会打破手性对称性吗
我个人的理解是,手征对称性会更强调两个子系统或两个子晶格,中心反演对称性则更强调几何结构。破坏石墨烯的中心反演对称性大概率会打破手性对称性吧,但我不确定是否是严格的,或者是否可以通过设计一个超胞作为反例,我没详细考虑和证明过,可以参考 2013 - Bernevig and Hughes - Topological Insulators and Topological Superconductors 这本书的第七章。
谢谢关老师的回复,我找到了一些关于跟子晶格sublattices关联的Bipartite lattices相关资料https://phsites.technion.ac.il/eric/wp-content/uploads/sites/6/2020/07/Amit_Goft-MSc_Thesis-compressed.pdf,对于理解子晶格对称性有很大帮助
在非厄米情况下 Chiral Symmetry 和Sublattice Symmetry不等价的,这在一些非厄米综述中明确提到过。
请问老师是在哪看见的综述,能分享一下吗
我也很好奇3*3的三能级哈密顿量的手征对称性问题,是否三维或者奇数维哈密顿量不能定义手征对称性(没有手征对称性)?
这个我不大清楚。我个人感觉是是没有的,或者只是解耦合的某个子系统中有。
3*3的系统可以定义generalized chiral symmetry
您好,请问关于3*3的generalized chiral symmetry是否有参考文献呢?谢谢
三格点 Generalized Chiral Symmetry 可以参考 Ni X., Weiner M., Alu A. and Khanikaev A. B., Nature materials, 18 (2019) 113.
老师,我最近在看文献的过程中遇到一个8*8的哈密顿量,利用文章给出的手征对称性对它进行幺正变换后有如您文章所说的对角元是两个4*4的0矩阵,反对角元是两个4*4的矩阵。但接下来我想重复出文章给出的能量的表达式(用符号表示的),但是对于这两个4*4的矩阵,文章提到这个体系有4个子晶格,且存在时间反演对称性,可我不知道接下来该如何下手去求解能量的表达式。想问一下老师在这方面能否给我一点建议?
老师您好,在很多地方,手征对称性的算符写为粒子空穴算符和时间反演算符乘积的形式 C=P T, P T作用在不同的空间tau、sigma。请问一下,PT和泡利算符sigma_z是如何等价的?
如果是作用在同一个空间上,PT和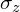 是等价的。因为
是等价的。因为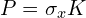 ,
, 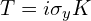 ,所以
,所以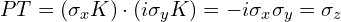 。你说的作用在不同空间,我不大清楚,如果是张量积的形式,只会得到四维的矩阵。
。你说的作用在不同空间,我不大清楚,如果是张量积的形式,只会得到四维的矩阵。
谢谢您的回答,我看的文章是Chiu et al. "Classification of topological quantum matter with symmetries." RMP (2016), 在您文中参考文献[3]中也有提及,大致是说T作用在自旋空间,P作用在粒子空穴空间 ,手征对称τ1σ2Hτ1σ2 = −H。好像Nambu表象下和如SSH模型的情况不太一样。
嗯,大概意思是差不多的,表达形式可能有的会不一样。手征对称性算符是和哈密顿量反对易的幺正算符,而粒子空穴算符和时间反演算符乘积刚好可以满足。
关老师您好!
我想问一下,对于3带及以上的手征对称哈密顿量,该如何求得对应的手征算符的矩阵呢?
三维的我不大了解。对于偶数维的,如果具有手征对称性,总可以幺正变换到左下和右上相互厄密共轭的形式。手征算符可以写成sigma_z和单位矩阵张量积的形式。
我看有的文章手特算符是单位矩阵和sigma_y的张量积啊
在不同表象下的形式可能会有点不同,具体以文章中的为准。常见的是sigma_z的形式
请问找到怎么求奇数维手征对称性算符的方法了吗?我也遇到了同样的问题,不过是5条能带