电子电流密度和空穴电流密度分别为:
![]()
![]()
在表达式内部中,前者是漂移电流,后者是扩散电流。
总电流密度为:![]()
符号说明:
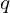 :基本电荷;
:基本电荷;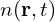 :电子浓度(单位体积内的电子数);
:电子浓度(单位体积内的电子数);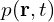 :空穴浓度;
:空穴浓度;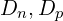 :电子和空穴的扩散系数;
:电子和空穴的扩散系数;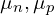 :电子和空穴的迁移率;
:电子和空穴的迁移率;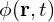 :静电势(电场
:静电势(电场 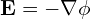 );
);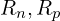 :净复合-产生率;
:净复合-产生率;
漂移-扩散方程(Drift-Diffusion Equation),即连续性方程为:
![]()
![]()
泊松方程(电势 ![]() 并非独立变量,需通过泊松方程与载流子浓度耦合):
并非独立变量,需通过泊松方程与载流子浓度耦合):
![]()
这里,施主提供的是可移动的负电荷(电子),但它自己留下了正电荷。
符号说明:
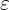 :材料介电常数;
:材料介电常数;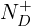 :电离施主浓度;
:电离施主浓度;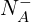 :电离受主浓度;
:电离受主浓度;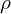 :净电荷密度。
:净电荷密度。
扩散系数与迁移率通过爱因斯坦关系关联:
![]()
符号说明:
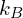 :玻尔兹曼常数;
:玻尔兹曼常数;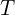 :绝对温度(单位:K)。
:绝对温度(单位:K)。
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】