考虑经典粒子体系(如气体分子、电子等),定义单粒子分布函数:![]()
在 t 时刻,粒子出现在相空间体元 ![]() 内的粒子数为:
内的粒子数为:![]()
玻尔兹曼输运方程(Boltzmann Transport Equation, BTE)本质上是一个相空间连续性方程,相空间中的粒子数守恒意味着:
![]()
展开全导数:
![]()
代入牛顿运动方程:
![]()
这是无碰撞的玻尔兹曼输运方程。
真实体系中,粒子会发生碰撞,使分布函数发生变化:
![]()
所以:
![]()
这是玻尔兹曼输运方程的一般形式。
如果只考虑二体碰撞,以及分子混沌假设(Stosszahlansatz):![]()
碰撞项可以写为(这里不展开讨论和证明):
![]()
其中:
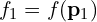 ,
,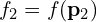
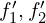 :碰撞后的分布
:碰撞后的分布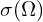 :微分散射截面
:微分散射截面
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】