这是之前的一篇:以一维链为例子说明能带折叠(附Python代码)。
本篇讨论的前提是已知能带折叠次数,同时已知折叠前的能带和折叠后的能带。通过速度和能量在折叠前和折叠后的一致性,可找到它们的对应关系。
为了简洁和避免重复,这里的代码用到Guan软件包中的函数:https://py.guanjihuan.com,根据函数名可以大概看出来实现什么功能。如果有需要知道函数的详细内容,可看对应的源码。
Python代码如下(以单链为例):
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/27605
"""
import guan
import numpy as np
# one dimensional chain model
unit_cell = 0
hopping = 1
hamiltonian_function_1 = guan.one_dimensional_fourier_transform_with_k(unit_cell, hopping)
k_array_1 = np.linspace(-np.pi, np.pi, 520)
eigenvalue_array_1 = guan.calculate_eigenvalue_with_one_parameter(k_array_1, hamiltonian_function_1)
# guan.plot(k_array_1, eigenvalue_array_1, xlabel='k', ylabel='E', style='k', title='one dimensional chain model')
# n times band folding
n = 7
unit_cell = np.zeros((n, n))
for i0 in range(int(n)):
for j0 in range(int(n)):
if abs(i0-j0)==1:
unit_cell[i0, j0] = 1
hopping = np.zeros((n, n))
hopping[0, n-1] = 1
k_array_2 = np.linspace(-np.pi, np.pi, 500)
hamiltonian_function_2 = guan.one_dimensional_fourier_transform_with_k(unit_cell, hopping)
eigenvalue_array_2 = guan.calculate_eigenvalue_with_one_parameter(k_array_2, hamiltonian_function_2)
# guan.plot(k_array_2, eigenvalue_array_2, xlabel='k', ylabel='E', style='k', title='%i times band folding'%n)
### 以下通过速度和能量查找能带折叠前后的对应关系
# 获取速度
velocity_array_1 = []
for i0 in range(k_array_1.shape[0]-1):
velocity_1 = (eigenvalue_array_1[i0+1]-eigenvalue_array_1[i0])/(k_array_1[i0+1]-k_array_1[i0])
velocity_array_1.append(velocity_1)
# 获取速度
velocity_array_2 = []
for i0 in range(k_array_2.shape[0]-1):
velocity_2 = (eigenvalue_array_2[i0+1]-eigenvalue_array_2[i0])/(k_array_2[i0+1]-k_array_2[i0])
velocity_array_2.append(velocity_2*n)
plt_1, fig_1, ax_1 = guan.import_plt_and_start_fig_ax()
plt_2, fig_2, ax_2 = guan.import_plt_and_start_fig_ax()
for i00 in range(n):
k_array_new_2 = []
k_array_new_1 = []
index_array_new_2 = []
index_array_new_1 = []
for i0 in range(k_array_2.shape[0]-1):
for j0 in range(k_array_1.shape[0]-1):
if abs(eigenvalue_array_2[i0][i00]-eigenvalue_array_1[j0])<1e-2 and abs(velocity_array_2[i0][i00]-velocity_array_1[j0])<1e-2:
k_array_new_2.append(k_array_2[i0])
k_array_new_1.append(k_array_1[j0])
index_array_new_2.append(i0)
index_array_new_1.append(j0)
if i00 == 0:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*r')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*r')
elif i00 == 1:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*b')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*b')
elif i00 == 2:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*g')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*g')
elif i00 == 3:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*c')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*c')
elif i00 == 4:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*m')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*m')
elif i00 == 5:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*y')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*y')
else:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1], style='*k')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*k')
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, [], [], xlabel='k', ylabel='E', title='one dimensional chain model')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, [], [], xlabel='k', ylabel='E', title='%i times band folding'%n)
plt_1.show()
plt_2.show()运行结果:
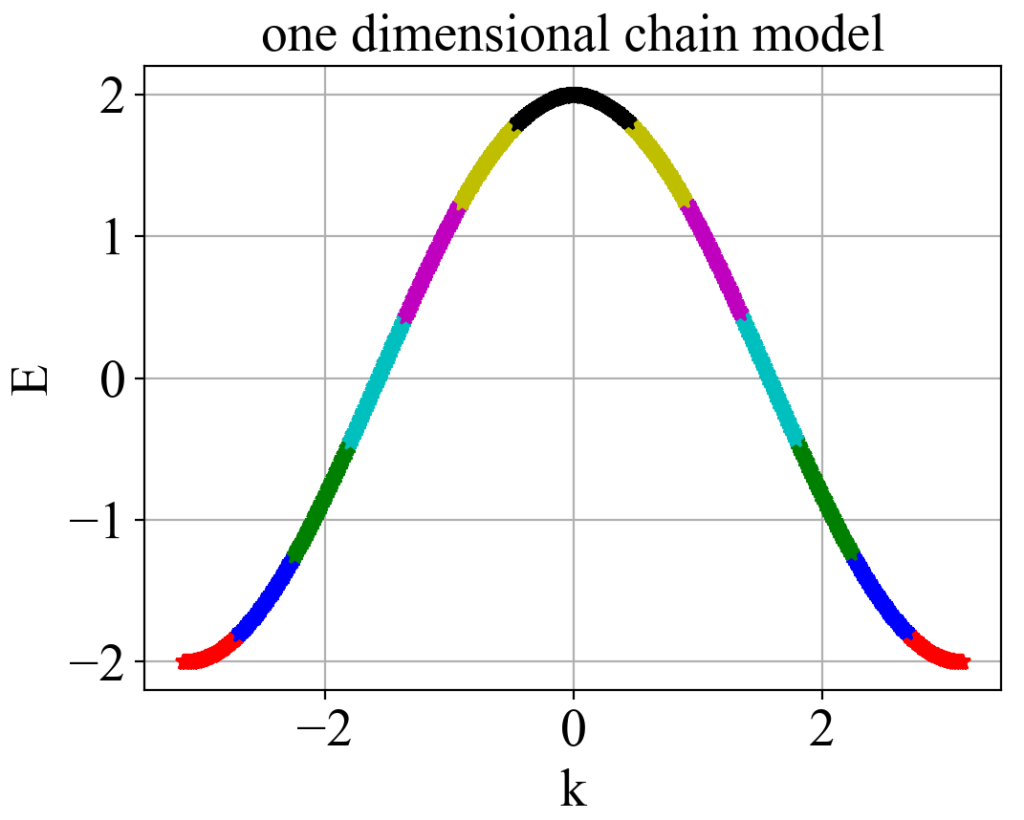
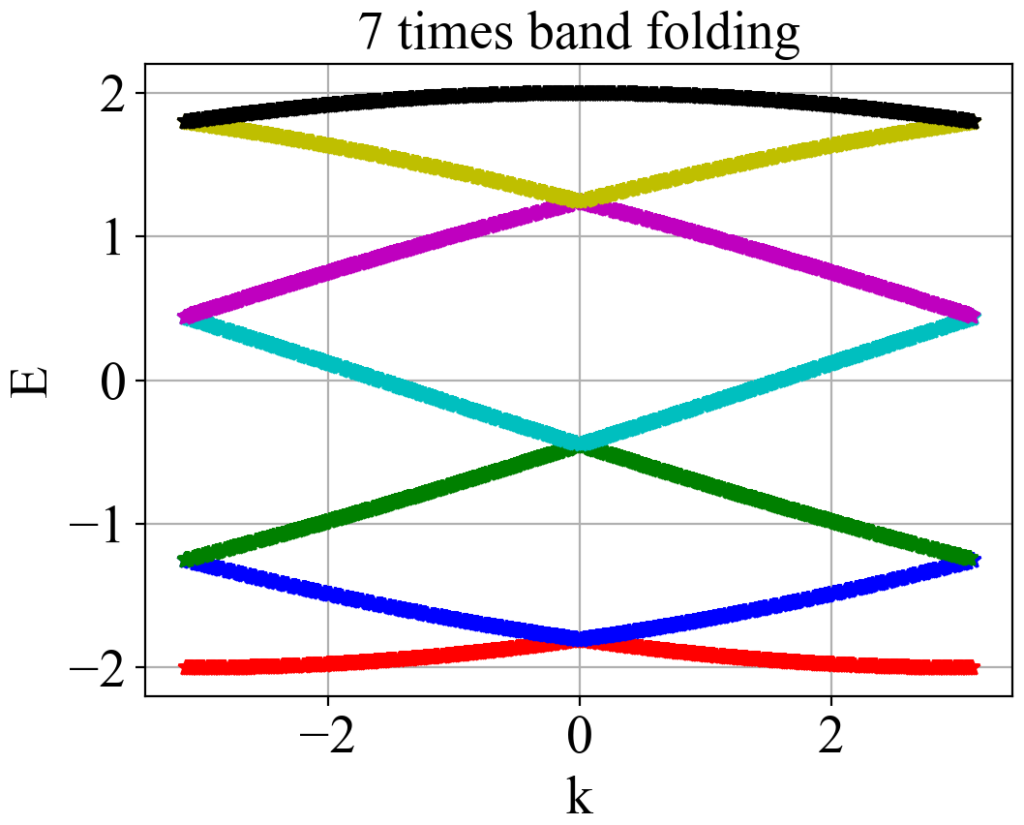
如果是多带的情况,也是可以处理的。以双链为例,Python代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/27605
"""
import guan
import numpy as np
# double chains model with different potentials
unit_cell = np.array([[0, 0], [0, 0.5]])
hopping = np.eye(2)
hamiltonian_function_1 = guan.one_dimensional_fourier_transform_with_k(unit_cell, hopping)
k_array_1 = np.linspace(-np.pi, np.pi, 600)
eigenvalue_array_1 = guan.calculate_eigenvalue_with_one_parameter(k_array_1, hamiltonian_function_1)
# guan.plot(k_array_1, eigenvalue_array_1, xlabel='k', ylabel='E', style='k', title='double chains model with different potentials')
# n times band folding
n = 2
unit_cell = np.zeros((2*n, 2*n))
for i0 in range(int(n)):
for j0 in range(int(n)):
if abs(i0-j0)==1:
unit_cell[i0, j0] = 1
for i0 in range(int(n)):
unit_cell[n+i0, n+i0] = 0.5
for j0 in range(int(n)):
if abs(i0-j0)==1:
unit_cell[n+i0, n+j0] = 1
hopping = np.zeros((2*n, 2*n))
hopping[0, n-1] = 1
hopping[n, 2*n-1] = 1
hamiltonian_function_2 = guan.one_dimensional_fourier_transform_with_k(unit_cell, hopping)
k_array_2 = np.linspace(-np.pi, np.pi, 620)
eigenvalue_array_2 = guan.calculate_eigenvalue_with_one_parameter(k_array_2, hamiltonian_function_2)
# guan.plot(k_array_2, eigenvalue_array_2, xlabel='k', ylabel='E', style='k', title='%i times band folding'%n)
### 以下通过速度和能量查找能带折叠前后的对应关系
# 获取速度
velocity_array_1 = []
for i0 in range(k_array_1.shape[0]-1):
velocity_1 = (eigenvalue_array_1[i0+1]-eigenvalue_array_1[i0])/(k_array_1[i0+1]-k_array_1[i0])
velocity_array_1.append(velocity_1)
# 获取速度
velocity_array_2 = []
for i0 in range(k_array_2.shape[0]-1):
velocity_2 = (eigenvalue_array_2[i0+1]-eigenvalue_array_2[i0])/(k_array_2[i0+1]-k_array_2[i0])
velocity_array_2.append(velocity_2*n)
dim = 2 # 维度为两倍
plt_1, fig_1, ax_1 = guan.import_plt_and_start_fig_ax()
plt_2, fig_2, ax_2 = guan.import_plt_and_start_fig_ax()
for j00 in range(dim):
for i00 in range(n*dim):
k_array_new_2 = []
k_array_new_1 = []
index_array_new_2 = []
index_array_new_1 = []
for i0 in range(k_array_2.shape[0]-1):
for j0 in range(k_array_1.shape[0]-1):
if abs(eigenvalue_array_2[i0][i00]-eigenvalue_array_1[j0][j00])<1e-2 and abs(velocity_array_2[i0][i00]-velocity_array_1[j0][j00])<1e-2:
k_array_new_2.append(k_array_2[i0])
k_array_new_1.append(k_array_1[j0])
index_array_new_2.append(i0)
index_array_new_1.append(j0)
if i00 == 0 and j00 == 0:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*r')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*r')
elif i00 == 0 and j00 == 1:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*b')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*b')
elif i00 == 1 and j00 == 0:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*g')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*g')
elif i00 == 1 and j00 == 1:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*c')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*c')
elif i00 == 2 and j00 == 0:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*m')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*m')
elif i00 == 2 and j00 == 1:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*y')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*y')
else:
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, k_array_new_1, eigenvalue_array_1[index_array_new_1, j00], style='*k')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, k_array_new_2, eigenvalue_array_2[index_array_new_2, i00], style='*k')
guan.plot_without_starting_fig_ax(plt_1, fig_1, ax_1, [], [], xlabel='k', ylabel='E', title='double chains model with different potentials')
guan.plot_without_starting_fig_ax(plt_2, fig_2, ax_2, [], [], xlabel='k', ylabel='E', title='%i times band folding'%n)
plt_1.show()
plt_2.show()运行结果:
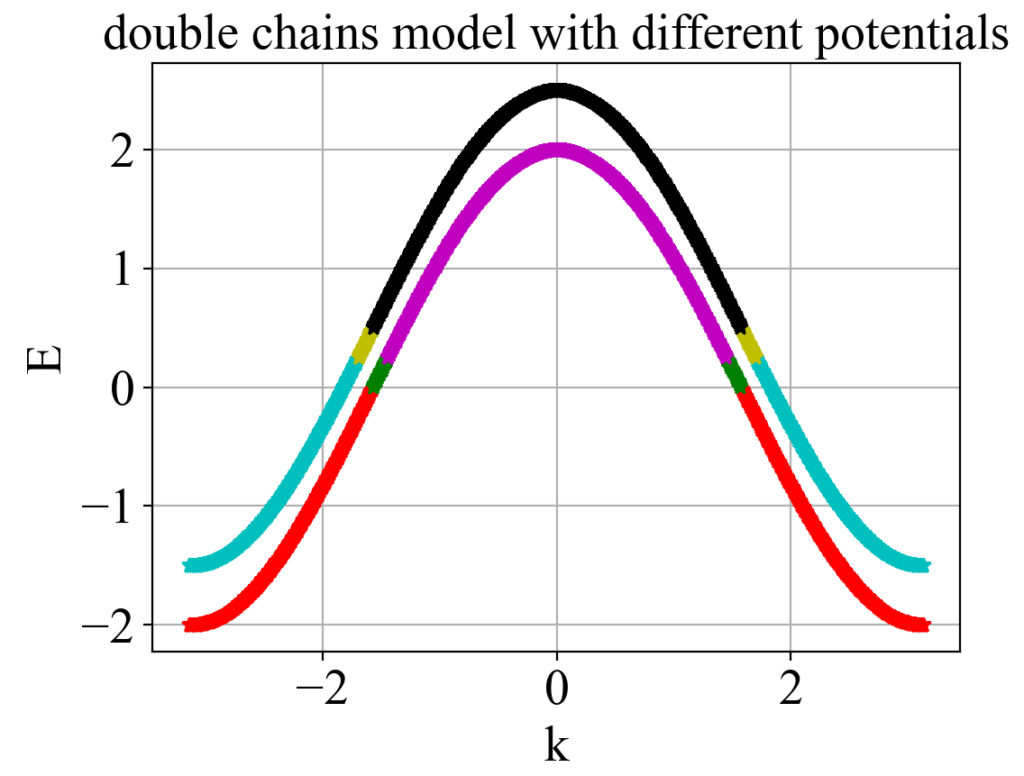
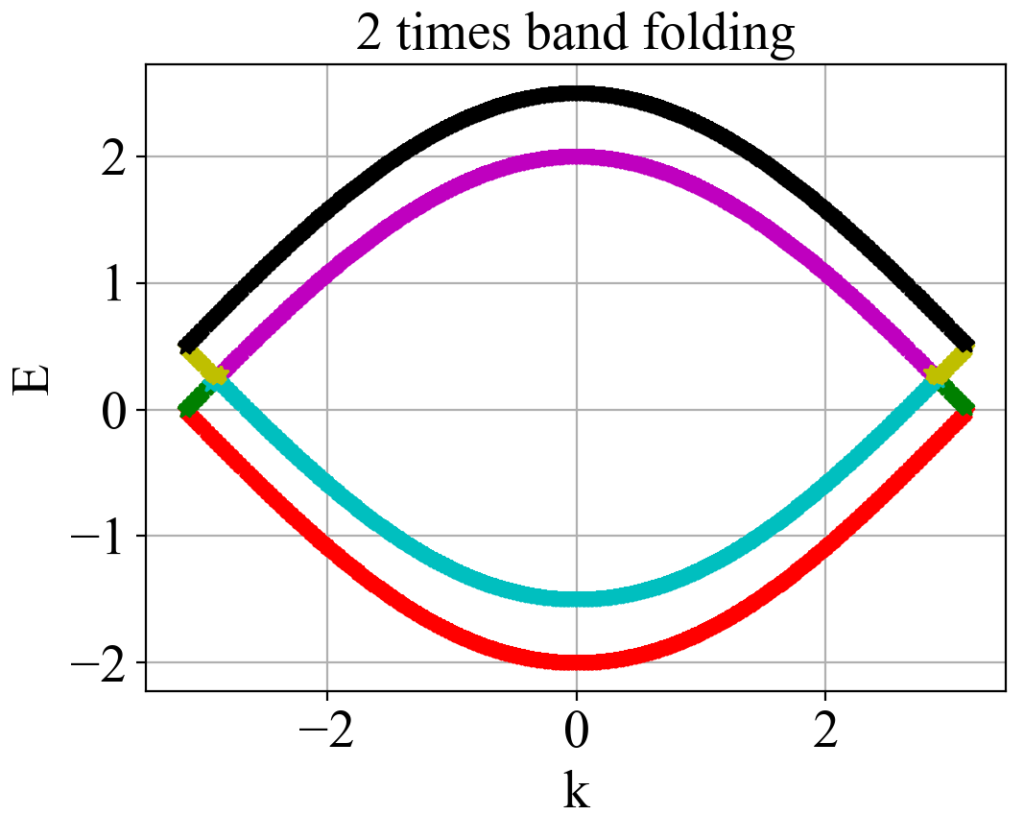
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】