在乐理中有以下的音程概念:
- 极完全协和音程:纯一度,纯八度
- 完全协和音程:纯四度,纯五度
- 不完全协和音程:大小三,大小六
- 极不协和音程:大小二、大小七以及所有的增,减,倍增,倍减音程。
这里给出三种音律中音阶频率的比例关系,从而直观了解不同音程给人以不同感受的物理机制。
一、五度相生律/三分损益律
管仲的三分损益律(中国)产生五个音:“宫、商、角、徵、羽”(读音为gōng shāng jué zhǐ yǔ),类似简谱中的 1、2、3、5、6。即宫等于 1(Do),商等于 2(Re),角等于 3(Mi),徵等于 5(Sol),羽等于 6(La),亦称作五音。可以参考:音乐也有科学道理?哆唻咪到底是咋定的?李永乐老师讲乐理知识。
毕达哥拉斯的五度相生律(西方)规定五度音的频率之比为 2:3,其他音程都由若干个五度产生。这里讲五度相生律的方法。
假设 Do(1,宫)的频率为 ![]() ,向上推五度有:
,向上推五度有:
- Sol(5,徵)的频率为
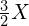 。
。 - Re(2,商)为
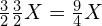 ,超过了一个八度的频率
,超过了一个八度的频率 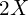 ,因为一个八度的频率比刚好是 2 倍关系,所以 Re 的频率为
,因为一个八度的频率比刚好是 2 倍关系,所以 Re 的频率为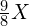 。
。 - La(6,羽)的频率为
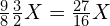 。
。 - Mi(3,角)为
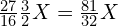 ,超过了一个八度的频率
,超过了一个八度的频率 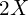 ,因为一个八度的频率比刚好是 2 倍关系,所以 Mi 的频率为
,因为一个八度的频率比刚好是 2 倍关系,所以 Mi 的频率为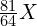 。
。 - Ti(7)的频率为
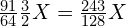 。
。
向下推五度有:
- Fa(4)为
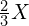 ,低于
,低于 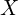 ,因为一个八度的频率比刚好是 2 倍关系,所以 Fa 的频率为
,因为一个八度的频率比刚好是 2 倍关系,所以 Fa 的频率为 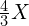 。
。 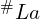 或
或 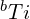 (
(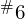 或
或 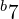 )为
)为 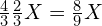 ,低于
,低于 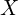 ,因为一个八度的频率比刚好是 2 倍关系,所以
,因为一个八度的频率比刚好是 2 倍关系,所以 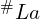 或
或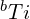 的频率为
的频率为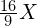 。
。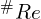 或
或 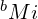 (
(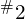 或
或 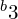 )的频率为
)的频率为 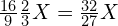 。
。 或
或 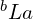 (
(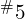 或
或 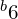 )为
)为 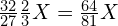 ,低于
,低于 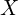 ,因为一个八度的频率比刚好是 2 倍关系,所以
,因为一个八度的频率比刚好是 2 倍关系,所以 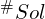 或
或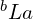 的频率为
的频率为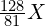 。
。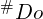 或
或 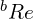 (
(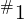 或
或 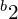 )的频率为
)的频率为 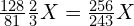 。
。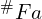 或
或 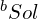 (
(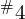 或
或 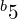 )的频率为
)的频率为 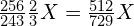 ,低于
,低于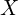 ,因为一个八度的频率比刚好是 2 倍关系,所以
,因为一个八度的频率比刚好是 2 倍关系,所以 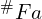 或
或 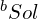 的频率为
的频率为 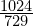 。
。
根据评论区网友的评论,这里补充一个说明:F 的下方五度是 bB(从 F 往下数五个音级:F-E-D-C-bB),#D 的上方五度是 #A(从#D往上数五个音级:#D-#E-#F-#G-#A)。bB 到 F 是纯五度(7个半音,协和音程),#A 到 F 是减六度(7个半音,不协和音程)。虽然 bB 和 #A 在十二平均律中是同一个音高,但在乐理中,它们具有不同的音级意义,解决倾向不同(bB 常下行解决,#A 常上行解决)。
所以需要注意的是:上面的向下推五度的记号要做一个取舍,我这里的写法只表示的是某个音高,不做区分和修改。关于更加详细的乐理知识,可阅读相关的教科书。
总结为动图:
该图片来源于参考资料[7]。
总结为表格:
| 音阶 | |||||||||||||
| 频率 |
二、纯律
纯律与五度相生律不同的是,除了规定纯五度音程频率之比为 2:3 以外,同时规定构成大三度的两个音频率比为 4:5,这样制定出各个音高。这时候频率可以变成更加简单的整数比,声音听起来会更“纯”一点。
由于既考虑了比值2:3,又考虑了比值4:5,所以产生 12 音阶的纯律会比较复杂一些,参照:知乎:为什么找不到 12 音阶的纯律?。
这里给出 7 音阶的纯律(不详细推导了,有变化的是 ![]() ,
,![]() ,
,![]() 三个音):
三个音):
| 音阶 | ||||||||
| 五度相生律的频率 | ||||||||
| 纯律的频率 |
三、十二平均律
上面两种音律都不好转调,当换一个调后比值会全乱掉,而十二平均律就没有转调这个问题。将 ![]() 频率和
频率和 ![]() 频率之间的区域按比例十二等分,相邻的两个音的频率倍数为:
频率之间的区域按比例十二等分,相邻的两个音的频率倍数为:![]() 。
。
总结为表格:
| 音阶 | |||||||||||||
| 频率 |
四、七个音阶的频率数值
Python 代码为:
print('音阶',' ','五度相生律',' ','纯律',' ','十二平均律')
print('Do %13.5f %13.5f %13.5f'%(1,1,1))
print('Re %13.5f %13.5f %13.5f'%(9/8,9/8,2**(2/12)))
print('Mi %13.5f %13.5f %13.5f'%(81/64,5/4,2**(4/12)))
print('Fa %13.5f %13.5f %13.5f'%(4/3,4/3,2**(5/12)))
print('Sol%13.5f %13.5f %13.5f'%(3/2,3/2,2**(7/12)))
print('La %13.5f %13.5f %13.5f'%(27/16,5/3,2**(9/12)))
print('Ti %13.5f %13.5f %13.5f'%(243/128,15/8,2**(11/12)))
print('Do %13.5f %13.5f %13.5f'%(2,2,2))运行结果为:
音阶 五度相生律 纯律 十二平均律
Do 1.00000 1.00000 1.00000
Re 1.12500 1.12500 1.12246
Mi 1.26562 1.25000 1.25992
Fa 1.33333 1.33333 1.33484
Sol 1.50000 1.50000 1.49831
La 1.68750 1.66667 1.68179
Ti 1.89844 1.87500 1.88775
Do 2.00000 2.00000 2.00000写成表格形式:
| 音阶 | 五度相生律 | 纯律 | 十二平均律 |
| Do | 1.00000 | 1.00000 | 1.00000 |
| Re | 1.12500 | 1.12500 | 1.12246 |
| Mi | 1.26562 | 1.25000 | 1.25992 |
| Fa | 1.33333 | 1.33333 | 1.33484 |
| Sol | 1.50000 | 1.50000 | 1.49831 |
| La | 1.68750 | 1.66667 | 1.68179 |
| Ti | 1.89844 | 1.87500 | 1.88775 |
| Do | 2.00000 | 2.00000 | 2.00000 |
五、三种音律的对比图
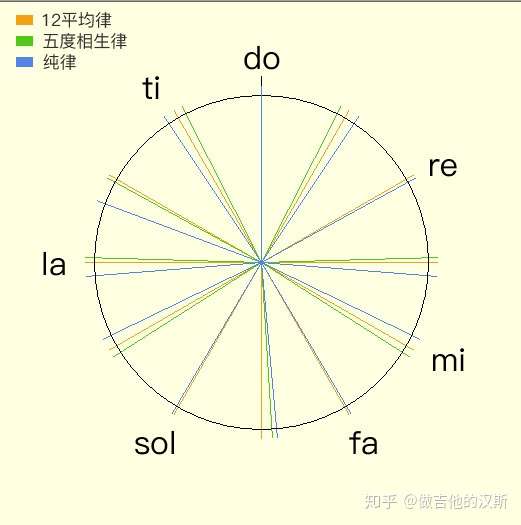
该图片来源于参考资料[7]
参考资料:
[1] 百度百科:协和音程
[3] 百度百科:宫商角徵羽
[4] 百度百科:三分损益法
[5] 百度百科:纯律
[6] 百度百科:十二平均律
[7] 知乎:请分别说明五度相生律、三分损益法、纯律、十二平均律这四种律制的优点及缺点?
[8] 知乎:纯律、五度相生律和十二平均律是如何产生的?三种律制之间有何关系?
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
指出一个乐理上的错误,F的下方五度是bB,#D的上方五度才是#A,这是完全不同的概念,两者音高也有不小的差异,不管是音程上还是音高上都不可以当作等音。bB-F是纯五度,协和音程,但#A-F是减六度,不协和音程,性质完全不同。
好的,感谢很专业地指出问题!我在博文中加上了补充说明。
我在计算时用【弦长】,不用【音程系数】
这样,在Excel显示就可以是 真分数,其倒数就是音程系数。很直观
(用音程系数,显示的是带分数,不直观,如您所示)
用弦长,计算音分数,与用音程系数计算 是一样的——绝对值相等。
推算纯律某音的频率,用 1/弦长 即可 (弦长与音程系数 互为倒数)
嗯,应该是可以的,弦长在视觉上更直观些。频率和弦长是反比关系,还需要一个系数。