以下是自己的一些群论笔记。
1. 群的定义
集合![]() 称为群,如果
称为群,如果![]() 中的元素满足以下四个条件:
中的元素满足以下四个条件:
- 封闭性:
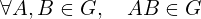
- 结合律:
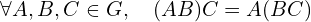
- 恒元:
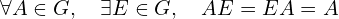
- 逆元:
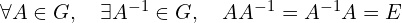
说明:这里的“元素”可以是任何的客体,“乘积”也可以是任意的运算法则。有限群中元素的个数被称为有限群的阶。
2. 阿贝尔群和非阿贝尔群
阿贝尔群:![]() (“乘积”可交换)
(“乘积”可交换)
非阿贝尔群:![]() (“乘积”不可交换)
(“乘积”不可交换)
3. 子群
定义:如果群![]() 中某些元素的集合(子集合)本身形成一个群
中某些元素的集合(子集合)本身形成一个群![]() ,那么该群
,那么该群![]() 称为群
称为群![]() 的子群,记为
的子群,记为![]() 。
。
显然,群本身![]() 和恒元
和恒元![]() 都是群
都是群![]() 的子群。
的子群。
4. 循环群
定理:在有限群G中,![]() ,存在一个最小的整数
,存在一个最小的整数![]() ,使得
,使得![]() 。其中,n称为群元(元素)A的阶。
。其中,n称为群元(元素)A的阶。
证明过程:因为是有限群,所以元素A乘积到一定次数后,一定会回到某个元素上。令该元素为![]() ,其中
,其中![]() 。假设
。假设![]() ,可以进一步写为
,可以进一步写为![]() ,因此得到
,因此得到![]() 。
。
有了以上的定理,可以知道![]() 的某
的某![]() 次方会得到恒元,这时候再乘一个
次方会得到恒元,这时候再乘一个![]() 就回到的自身,形成了一个循环。
就回到的自身,形成了一个循环。
循环群的定义:由元素![]() 和元素
和元素![]() 的幂次构成的群,称为由A生成的循环群,记作:
的幂次构成的群,称为由A生成的循环群,记作:![]() ,其中
,其中![]() 表示循环群的阶,
表示循环群的阶,![]() 为循环群的生成元。只有循环群,生成元的阶才等于群的阶。
为循环群的生成元。只有循环群,生成元的阶才等于群的阶。
显然,循环群是阿贝尔群。
5. 有限群的乘法表
有限群中元素的“乘积”可以写成一个表格的形式,例如三阶循环群![]() :
:
6. 重排定理
重排定理:![]() 是群
是群![]() 中任意的一个元素,把这个元素
中任意的一个元素,把这个元素![]() 和群
和群![]() 中所有的元素“相乘”(左乘或右乘),得到新的元素集合,这个集合仍然是群
中所有的元素“相乘”(左乘或右乘),得到新的元素集合,这个集合仍然是群![]() 。表达式可写为:
。表达式可写为:![]() 。
。
证明略,证明过程可看参考资料。
该定理说明了在乘法表的每一行或列中,所有元素只能出现一次。也就是每一行或列都是所有元素的重排。
7. 陪集(coset)
定义:设![]() 是群
是群![]() 的子群,在群
的子群,在群![]() 中选取一个不在子群
中选取一个不在子群![]() 元素
元素![]() ,把它左乘或右乘在子群
,把它左乘或右乘在子群![]() 上,得到群
上,得到群![]() 的两个子集:
的两个子集:![]() 称为子群
称为子群![]() 的左陪集,
的左陪集,![]() 称为子群
称为子群![]() 的右陪集。
的右陪集。
陪集的性质:
(1)陪集与子群![]() 没有公共元素。证明:以左陪集为例,假设左陪集
没有公共元素。证明:以左陪集为例,假设左陪集![]() 和子群
和子群![]() 存在公共元素,即
存在公共元素,即![]() ,那么
,那么![]() ,与陪集的定义中
,与陪集的定义中![]() 矛盾。证毕。
矛盾。证毕。
(2)可进一步得到:陪集中不包含恒元。也就是说陪集只是一个集合,不是一个群(不满足群的定义条件),更不是群G的子群。
(3)陪集定理:子群的两个右陪集(或左陪集),要么有完全相同的元素,要么没有任何公共元素。证明略。
(4)拉格朗日定理:群![]() 的阶
的阶![]() 一定是子群
一定是子群![]() 的阶
的阶![]() 的整数倍。证明略。
的整数倍。证明略。
8. 不变子群(正规子群)
定义:若群![]() 的子群
的子群![]() 的所有左陪集都与对应的右陪集相等,则称子群
的所有左陪集都与对应的右陪集相等,则称子群![]() 为不变子群。可以写成
为不变子群。可以写成![]() ,其中
,其中![]() 。
。
显然,阿贝尔群的所有子群都是不变子群。
9. 共轭元素与类
共轭元素的定义:如果存在![]() ,使得
,使得![]() ,则称元素
,则称元素![]() 和
和![]() 共轭。
共轭。
共轭元素性质:
(1)对称性:![]() ,则
,则![]() ,共轭是相互的。
,共轭是相互的。
(2)传递性:![]() ,
,![]() ,于是有
,于是有![]() 。
。
类的定义:群![]() 的所有相互共轭的元素集合组成
的所有相互共轭的元素集合组成![]() 的一个类。
的一个类。
10. 商群
不变子群H及其所有陪集作为复元素的集合,若按复元素的乘积规则满足群的四个条件,该群称为群![]() 关于不变子群H的商群,记作
关于不变子群H的商群,记作![]() 。
。
11. 群的同构关系(isomorphic)
若群![]() 和
和![]() 的所有元素间都按某种规则存在一一对应的关系(双射),且它们的乘积也按同一规则一一对应,则称两群同构。
的所有元素间都按某种规则存在一一对应的关系(双射),且它们的乘积也按同一规则一一对应,则称两群同构。
12. 群的同态关系(homomorphic)
若群![]() 和
和![]() 的所有元素间都按某种规则存在一多对应关系(满射),即群
的所有元素间都按某种规则存在一多对应关系(满射),即群![]() 中任一元素都唯一对应
中任一元素都唯一对应![]() 中的一个确定元素,
中的一个确定元素,![]() 中任一元素至少对应
中任一元素至少对应![]() 中一个元素,也可对应
中一个元素,也可对应![]() 中若干元素,且群元素的乘积也按同一规则一多对应,则称两群同态。
中若干元素,且群元素的乘积也按同一规则一多对应,则称两群同态。
说明:同态有方向性,即![]() 与
与![]() 同态,不一定
同态,不一定![]() 与
与![]() 同态。群
同态。群![]() 只反映了群
只反映了群![]() 的部分性质。
的部分性质。
参考资料:
[1] GroupTheory: Application to the Physics of Condensed Matter (M.S. Dresselhaus, G. Dresselhaus, A. Jorio)
[2] 国科大郭璐老师的《群论》课件
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】