这里的计算的方格子和石墨烯都是有长度,有宽度情况,即准零维的量子点。二维的情况可以参考这篇文献:二维晶格色散关系和态密度的紧束缚模型计算。
本篇的态密度是使用格林函数的方法来计算。在下面计算的结果可以发现:当长度和宽度足够长时,总态密度与费米能的关系接近于二维的情况(因为存在边缘态,所以结果也不一样完全相同)。
需要说明的是:虚数项 eta 的取值应该比较小,才是比较真实的态密度情况。当虚数项 eta 比较小时,态密度是离散的几个峰。在下面的计算中,虚数项 eta 的取值相对比较大,即 eta=0.1,目的是使得几个峰有相对大的展宽,使得态密度随着量子的尺寸增加更容易接近与二维的情况。实际上,当体系足够大时,多个峰也会连在一块,使得曲线连续。具体关于 eta 的讨论参考这篇:用格林函数计算态密度时费米能中虚部的取值。
一、方格子
代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4622
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
def hamiltonian(width=10, length=10): # 方格子哈密顿量
h = np.zeros((width*length, width*length))
# y方向的跃迁
for x in range(length):
for y in range(width-1):
h[x*width+y, x*width+y+1] = 1
h[x*width+y+1, x*width+y] = 1
# x方向的跃迁
for x in range(length-1):
for y in range(width):
h[x*width+y, (x+1)*width+y] = 1
h[(x+1)*width+y, x*width+y] = 1
return h
def main():
plot_precision = 0.01 # 画图的精度
Fermi_energy_array = np.arange(-5, 5, plot_precision) # 计算中取的费米能Fermi_energy组成的数组
dim_energy = Fermi_energy_array.shape[0] # 需要计算的费米能的个数
total_DOS_array = np.zeros((dim_energy)) # 计算结果(总态密度total_DOS)放入该数组中
h = hamiltonian() # 体系的哈密顿量
dim = h.shape[0] # 哈密顿量的维度
i0 = 0
for Fermi_energy in Fermi_energy_array:
print(Fermi_energy) # 查看计算的进展情况
green = np.linalg.inv((Fermi_energy+0.1j)*np.eye(dim)-h) # 体系的格林函数
total_DOS = -np.trace(np.imag(green))/pi # 通过格林函数求得总态密度
total_DOS_array[i0] = total_DOS # 记录每个Fermi_energy对应的总态密度
i0 += 1
sum_up = np.sum(total_DOS_array)*plot_precision # 用于图像归一化
plt.plot(Fermi_energy_array, total_DOS_array/sum_up, '-') # 画DOS(E)图像
plt.xlabel('费米能')
plt.ylabel('总态密度')
plt.show()
if __name__ == '__main__':
main()当长度为 10,宽度为 10 时,计算的结果为:
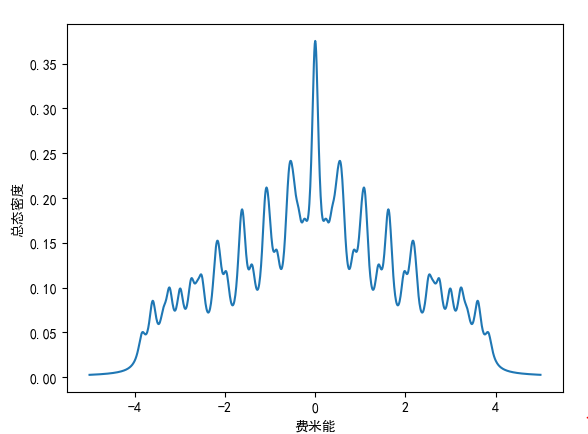
当长度为 20,宽度为 20 时,计算的结果为:
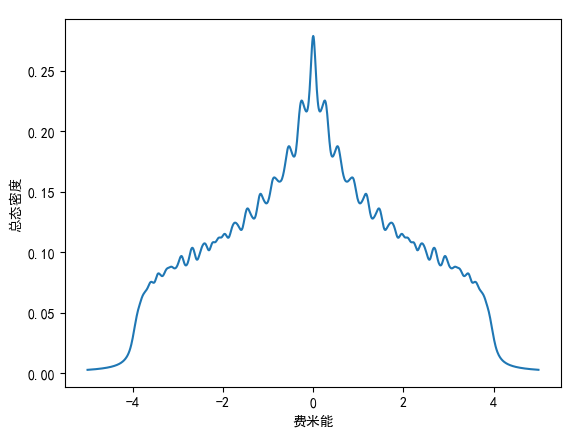
当长度为 30,宽度为 30 时,计算的结果为:
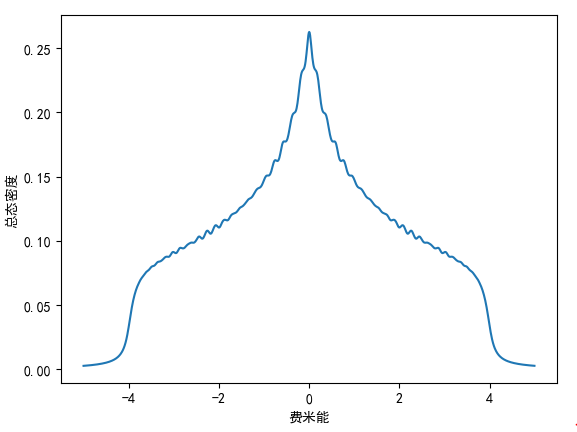
二、石墨烯(六角格子)
代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4622
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
def hamiltonian(width=8, length=8): # 石墨烯格子的哈密顿量。这里width要求为4的倍数
h = np.zeros((width*length, width*length))
# y方向的跃迁
for x in range(length):
for y in range(width-1):
h[x*width+y, x*width+y+1] = 1
h[x*width+y+1, x*width+y] = 1
# x方向的跃迁
for x in range(length-1):
for y in range(width):
if np.mod(y, 4)==0:
h[x*width+y+1, (x+1)*width+y] = 1
h[(x+1)*width+y, x*width+y+1] = 1
h[x*width+y+2, (x+1)*width+y+3] = 1
h[(x+1)*width+y+3, x*width+y+2] = 1
return h
def main():
plot_precision = 0.01 # 画图的精度
Fermi_energy_array = np.arange(-5, 5, plot_precision) # 计算中取的费米能Fermi_energy组成的数组
dim_energy = Fermi_energy_array.shape[0] # 需要计算的费米能的个数
total_DOS_array = np.zeros((dim_energy)) # 计算结果(总态密度total_DOS)放入该数组中
h = hamiltonian() # 体系的哈密顿量
dim = h.shape[0] # 哈密顿量的维度
i0 = 0
for Fermi_energy in Fermi_energy_array:
print(Fermi_energy) # 查看计算的进展情况
green = np.linalg.inv((Fermi_energy+0.1j)*np.eye(dim)-h) # 体系的格林函数
total_DOS = -np.trace(np.imag(green))/pi # 通过格林函数求得总态密度
total_DOS_array[i0] = total_DOS # 记录每个Fermi_energy对应的总态密度
i0 += 1
sum_up = np.sum(total_DOS_array)*plot_precision # 用于图像归一化
plt.plot(Fermi_energy_array, total_DOS_array/sum_up, '-') # 画DOS(E)图像
plt.xlabel('费米能')
plt.ylabel('总态密度')
plt.show()
if __name__ == '__main__':
main()当长度为 8,宽度为 8 时,计算的结果为:
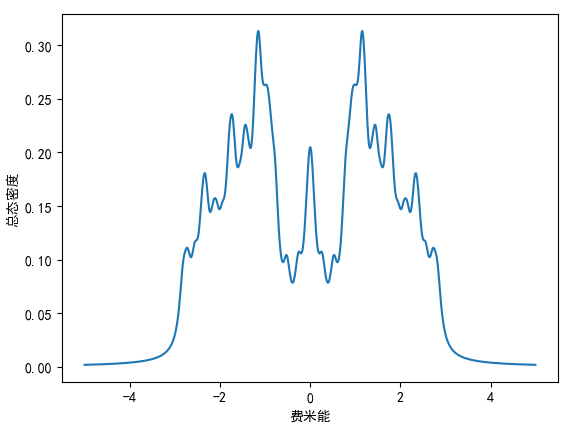
当长度为 20,宽度为 20 时,计算的结果为:
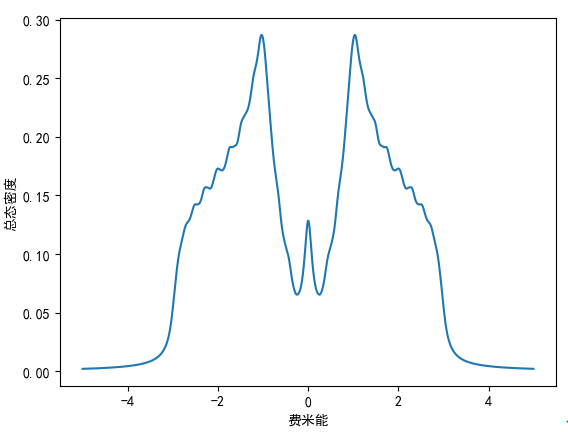
当长度为 32,宽度为 32 时,计算的结果为:
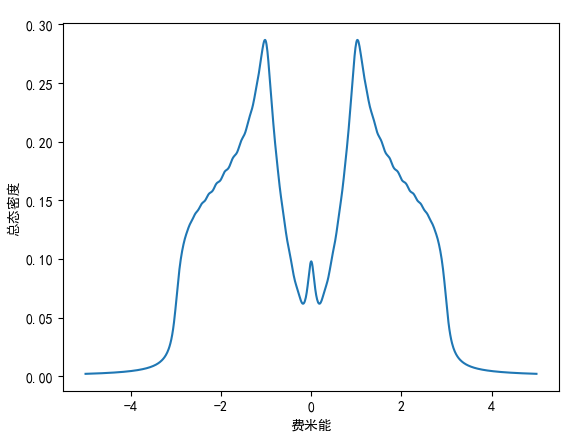
因为石墨烯的边缘态是在零能附近,所以这里可以很明显的看到边缘态的态密度。
参考资料:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
博主你好,如果把体系加上自旋,想要分别计算自旋向上和自旋向下的dos,需要如何修改dos的计算公式呢
看你把自旋自由度是加在哪个位置。如果是两个矩阵块,那么就取对应矩阵块的对角元。如果是将跃迁项和在位能项维度翻倍,那么就取对应自旋的对角元。
把自旋加在跃迁项和在位能项,是不是直接取格林函数上对应的自旋向上和自旋向下的矩阵元,然后用total_DOS = -np.trace(np.imag(green))/pi 公式分别计算dos
是的
好的 谢谢博主~
博主您好,我想确认一下自旋向上和自旋向下分别对应的是格林函数的哪部分矩阵元
这个跟你的哈密顿量中的编号以及自旋放在哪个位置有关。态密度的信息在格林函数的对角线上。
有对应的文献可以参考嘛
这个有很多文献吧。例如这篇中的第10式(不是自旋自由度,但表达式类似):Quasiparticle scattering interference in superconducting iron pnictides。
请问博主,六角格子的第一布里渊区对应的kx和ky的取值范围应该是什么样的呀
参考这两篇:
谢谢博主噜
博主您好,我想问一下,您石墨烯图像归一化那里,为什么乘了一个精度(0.01)?讲道理归一化不就是E对应的态密度除以总和么?那乘精度是怎么一回事?谢谢!
如果仅仅是简单的求和,那么取的点越多,分母越大,最后数值越小。
之所以乘一个精度,是因为对曲线积分时,有一个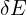 ,也就是计算的精度(或者说是步长)。
,也就是计算的精度(或者说是步长)。