《KAN: Kolmogorov-Arnold Networks》论文链接：https://arxiv.org/abs/2404.19756。
Kolmogorov-Arnold Networks（KANs）相对于传统的多层感知机（MLPs）主要具有以下优势：
- 高准确性：KANs能够通过更小的模型尺寸实现与大型MLPs相当或更高的精度。特别是在处理具有组合结构的数据时，KANs能够有效规避维数灾难，并且展现出更优的神经缩放律，即测试损失（test loss）随着模型参数数量N的增加而更快降低。
- 优越的可解释性：KANs采用的一维可学习样条函数作为激活函数，不仅提高了模型的直观可视化和分析能力，而且通过正则化和剪枝技术，KANs能够自动揭示数据的内在组合结构，这在科学探索中尤为宝贵。此外，研究人员可以与KANs进行交互，利用一系列技巧进一步提升模型的可解释性。
- 强大的连续学习能力：得益于局部基函数的样条表示，KANs展现出局部可塑性，这使得它们在处理连续学习任务时能够有效避免灾难性遗忘问题。
- 广泛的应用潜力：KANs结合了样条函数的精确性和神经网络的学习能力，不仅适用于数据拟合、偏微分方程求解等任务，而且有潜力成为人工智能与科学研究结合的基础模型。
然而，KANs也面临一些挑战和局限性：
- 模型的复杂性：引入可学习的样条函数使得KANs的设计和训练过程更加复杂，可能需要特殊的优化技术来处理。另外，虽然KANs的样条函数参数化提供了更高的表达能力，通常允许比MLPs更小的计算图，但在某些情况下，它们可能需要更多的参数来实现相同的性能。
- 网络结构的敏感性：与MLPs相比，KANs的性能可能对网络层数和宽度的选择更为敏感，需要更加精细的调参。
- 理论基础的深化：KANs目前仍缺乏对深层网络表达能力和泛化性能的深入理论分析和理解。
综上所述，KANs作为一种新兴的神经网络模型，通过有效地结合组合结构和单变量函数的优势，在准确性和可解释性方面展现了巨大潜力，并为AI与科学的结合提供了新的视角，但在理论基础、通用性和效率等方面仍需进一步研究和改进。
说明：以上由 AI 生成，使用的模型为 Claude + 文本提供 + 人工整理。
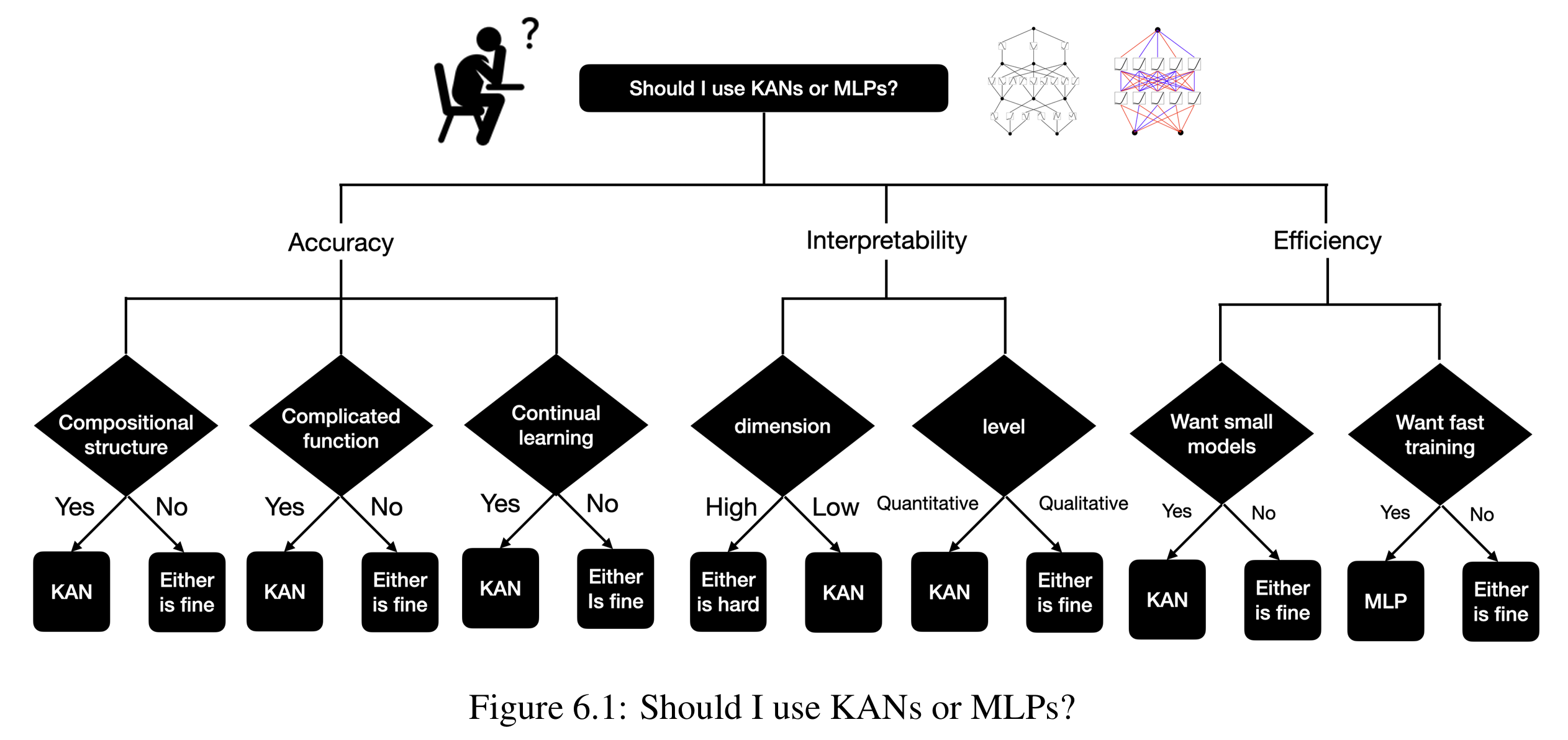
博主补充：该模型实现了从“参数网络（节点）”的学习到“函数网络（节点性状）”的学习的转变。优势是可解释性好，能够自动揭示数据的内在组合结构，有助于科学发现。局限性是模型复杂度更高，比较难搭建和训练，和传统的神经网络模型优化算法不完全兼容。
附上文章中的图：
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
