由泡利矩阵组成的哈密顿量的本征值

由泡利矩阵组成的哈密顿量一般形式：

$\begin{aligned}H&=a_0 \sigma_0 + a_1 \sigma_1 +a_2 \sigma_2+a_3 \sigma_3 \\&=\begin{pmatrix}a_0+a_3 & a_1-i a_2\\a_1+i a_2 & a_0-a_3\end{pmatrix}\end{aligned}$

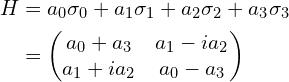
本征方程： $H|\psi\rangle = E|\psi\rangle$

本征值的形式为： $E=a_0 \pm \sqrt{a_1^2 +a_2^2+a_3^2}$

以上可自行推导或用Mathematica求解，MMA代码如下：

Clear["`*"]
H = ({{a0, 0}, {0, a0}}) + ({{a3, a1 - I*a2}, {a1 + I*a2, -a3}});
MatrixForm[H]
eigenvalue = MatrixForm[Simplify[Eigenvalues[H]]]
eigenvector = MatrixForm[Simplify[Eigenvectors[H]]]

运算结果：

参考资料：

[1] 泡利矩阵以及泡利矩阵的张量积

5,996 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

2 thoughts on “由泡利矩阵组成的哈密顿量的本征值”

老师好，有个问题。我的模型是7带，但是我mathematica好像不能做到解析解的基矢。在mathematica中大于五维(五次或以上的多项式方程)都不能得到代数解，这我该如何得到相应基矢并投影到上下离费米能级最近的两条带得到二维的哈密顿量。

guanjihuan说道：

2025年8月6日 08:53

具体操作我也不大熟悉。这边提供几个思路，仅供参考：

（1）直接采用数值投影的方法，不获取代数解的形式。
（2）使用 Schrieffer–Wolff 变换方法或者 Löwdin 微扰方法。
（3）对具有高对称性的体系，可以考虑 k⋅p 有效模型。

回复

由泡利矩阵组成的哈密顿量的本征值

Published by guanjihuan

2 thoughts on “由泡利矩阵组成的哈密顿量的本征值”

发表评论取消回复

Published by guanjihuan

2 thoughts on “由泡利矩阵组成的哈密顿量的本征值”

发表评论 取消回复

发表评论取消回复